一种基于条件信息熵的多目标代价敏感属性约简算法的研究
2014-03-27徐冰心陈慧萍
徐冰心,陈慧萍
(河海大学 物联网工程学院,江苏 常州 213022)
近年来,代价敏感属性约简是数据挖掘和机器学习领域的重要课题.现实生活中大多数数据的获取需要付出多种代价,例如,在医疗体检中,对于被检测者而言,他们需要花费金钱、时间以及其他的资源来获取自己的体检结果.已有算法[1-5]基本都是针对单目标进行优化.因此,有必要在多目标代价敏感学习的基础上对数据进行属性约简.属性约简的目的是在保证信息系统分类能力不变的前提下,删除冗余的属性.
在多目标代价敏感属性约简问题中,每个子目标函数均可体现其中的某一种代价.这些子目标函数之间往往是相互矛盾的,即某个子目标函数所对应的代价减少可能导致其他某个或多个子目标函数对应的代价增加,不可能使所有子目标函数所对应的代价都达到最小,只能对多个子目标函数进行平衡折中,寻找使每个子目标函数所对应的代价尽可能小的最优解集,即帕雷托最优解集[6].
代价敏感学习中多目标优化问题的研究还处于起步阶段,基于单目标代价敏感属性约简,本文提出了多目标代价敏感属性约简问题,并设计了一种简单高效的算法.该算法能较好地解决多目标代价敏感属性约简问题.
1 基本概念
1.1 多代价决策表(MC-DS)
定义1 多代价决策表是一个六元组:S=(U,C,D,V,I,C),其中,U为对象的集合也称论域,C为条件属性集合,D为决策属性集合,Va为属性a的值域,Ia:U→Va为信息函数,C={c1,c2,…,ck}是k种代价函数的集合,ci:C→R+∪0(i∈[1,k])表示第i种代价函数.简单起见,本文只考虑2种类型的代价,即测试代价和延迟代价.它们分别指为获得对象的属性值,进行测试所付出的金钱和时间代价.
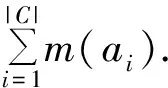
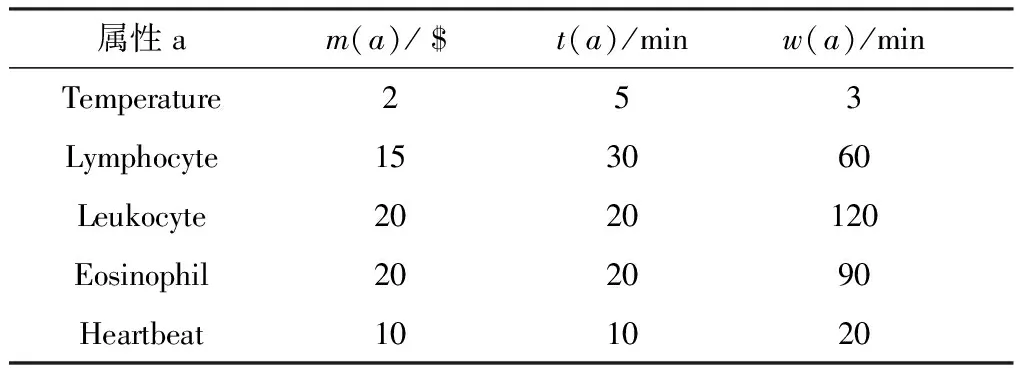
表1 典型的代价矢量
一项检测的等待时间通常可以和其它项检测的测试时间或等待时间重叠.例如,在等待Leukocyte结果的过程中,可以进行任何其它项测试.属性子集的延迟代价可以按照(1)式计算,其中,T_C表示一个属性子集的最小延迟代价,tj代表第j个测试的测试时间,wi代表第i个测试的等待时间,n是检测的项目数.
(1)
当各个测试以等待时间降序排列时,可获得最小延迟代价[7].可以结合下例予以解释.
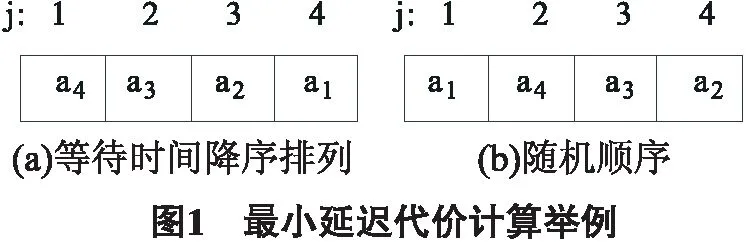
简单起见,从表1中选择4个测试项目Temperature,Lymphocyte,Leukocyte和Eosinophil,并分别用a1,a2,a3,a4表示.图1中,j代表测试顺序,图1(a)中的测试按等待时间降序排列;图1(b)中的测试是随机安排的.依据(2)式,图1(a)中测试的延迟代价T_C1为:
T_C01=t1+w1=t(a3)+w(a3)=20+120=140;
T_C02=t1+t2+w2=t(a3)+t(a4)+w(a4)=20+20+90=130;
T_C03=t1+t2+t3+w3=t(a3)+t(a4)+t(a2)+w(a2)=20+20+30+60=130;
T_C04=t1+t2+t3+t4+w4=t(a3)+t(a4)+t(a2)+t(a1)+w(a1)=20+20+30+5+3=78;
T_C1=max{T_C01,T_C02,T_C03,T_C04}=140.
其中,T_C01、T_C02、T_C03和T_C04分别代表第i(i∈[1,4])个测试的延迟代价.
同理,图1(b)中测试的延迟代价T_C2为165,T_C1明显小于T_C2.
通常情况下数据信息的获取都需要花费不同类型的代价,为简单起见,本文不考虑免费测试.
1.2 关联约简
属性约简是粗糙集研究中的关键问题之一.已有研究从不同的角度处理约简问题[8-11].本文采用基于条件信息熵的定义.
定义2S=(U,C,D,V,I)是一个决策表,当B⊆C时,H(D|B)表示B对于D的条件熵,对于任意的RC,若同时满足以下2个条件则为一个约简:
1)H(D|R)=H(D|C);
2)∀a∈R,H(D|R-{a})>H(D|C).
1.3 多目标代价敏感约简问题
定义3 设S是一个多代价决策表(MC-DS),Red={R1,R2,…,Rn}为S所有约简的集合,R表示MC-DS的帕雷托最优解集.若满足以下2个条件,则称任意的Ri优于Rj,记为Ri>Rj(i,j∈[1,n]):
1)∀p∈[1,k],cp(Ri)≤cp(Rj);
2)∀q∈[1,k],cq(Ri) 然而,有些约简是不可比的,即不存在Ri>Rj或者Ri 由此可见,Red(S)中的约简有些是可以比较的,有些是不可比较的,S所有约简之间就构成了偏序关系. 为了更好地说明S所有约简间的偏序关系,图2给出考虑3种代价的MC-DS中约简集Red={R1,R2,…,R9}元素间的偏序关系.为了简洁起见,分别用c1(R1)、c2(R1)和c3(R1)来表示这3种代价.从图中可以看出,第1层的4个约简对应的3种代价之间有如下关系:①c1(R1) 本文设计了一种简单高效的算法来解决多目标代价敏感属性约简问题.算法基本思想为:首先,利用条件信息熵计算决策表的所有约简,并将其存储起来以方便读取,由此可以节省大量的程序运行时间.然后,分别计算这些约简所对应的测试代价和延迟代价,根据这2种代价来比较对应的约简,并且移除那些代价高的约简,剩下的约简就是帕雷托最优解. 算法具体步骤: 输入:多代价决策表S={U,C,D,V,I,c,t,w}. 输出:帕雷托最优解集R. 步骤1 计算并存储多代价决策表的所有约简; 步骤2 根据这些约简所对应的测试代价和延迟代价,比较各个约简,并移除那些没有任何代价优势的约简; 步骤2.1 初始化2个数组,分别用来存储所有约简和被移除的约简; 步骤2.2 分别计算这些约简所对应的测试代价和延迟代价; 步骤2.3 依据各自对应的测试代价和延迟代价,将一个约简与其他约简进行比较; 步骤2.4 存储最优约简单,并计算其个数; 步骤2.5 返回R. 以UCI数据集Tic-tac-toe为例,该数据集有9个约简,分别用R1,R2,R3,R4,R5,R6,R7,R8和R9表示.算法的执行过程如表2所示. 表2 基于条件信息熵的多目标约简过程实例 Exclusion:R1,R2,R4,R6,R7,R8 ReturnR={R3,R5,R9} 测试代价和延迟代价分别用m(Ri)和t(Ri)(i∈[1,9])来表示.如果满足m(Ri)≥m(Rj),t(Ri)>t(Rj)或者m(Ri)>m(Rj),t(Ri)≥t(Rj)(i,j∈[1,9]且i≠j),那么,用“-1”表示Ri 为了测试本算法的有效性,从UCI数据库中分别选取实例和属性个数从低到高的4个数据集作为算例进行测试,见表3.由于这些数据集本身不含代价信息,分别利用均匀分布、正态分布和帕雷托分布分别为其产生测试代价、测试时间代价和等待时间代价,这3种代价均为100至 1 000 的随机整数.利用开源软件Coser[12]实现本算法,算法独立运行100次,并统计100次实验所得的帕雷托最优解的平均数目,以评价算法的收敛性和稳定性. 表3 UCI数据集 由于空间有限,在此只给出一部分的实验结果.图3中,测试代价、测试时间和等待时间分别服从帕雷托分布、正态分布和均匀分布.Mushroom数据集有292个约简,100次实验获得的平均帕累托最优解的数目是2.14.因此,Mushroom数据集的绝对基数是2.14,相对基数是2.14÷292≈0.007 33.同理,Voting数据集的绝对基数是1.09,相对基数是1.09÷3≈0.363;Zoo数据集的绝对基数是1.83,相对基数是1.83÷33≈0.055 4;Tic-tac-toe数据集的绝对基数是2.09,相对基数是2.09÷9≈0.232.由此可见,帕雷托最优解集的绝对基数和相对基数都很小. 由以上分析可得,该算法可有效地解决MOR问题,且数据集越大,算法的优势越明显.假设Mushroom数据集的所有约简代表实际应用系统中的292种不同的方案,通过多目标约简后仅剩下几种最优的方案供选择,由此,我们的算法可以更好地辅助用户做出方案的选择. 图4中,“U”、“N”和“B”分别代表均匀分布、正态分布和有界的帕雷托分布.实验中,考虑Mushroom数据集上的测试代价和延迟代价(测试时间和等待时间服从相同的分布).比如,“NB”中的第1个字母“N”代表测试代价的分布是正态分布,第2个字母“B”代表延迟代价中的测试时间和等待时间的分布均为帕雷托分布.每组实验过程中,保持分布不变,但代价为100到 1 000 的随机整数,算法独立运行100次,得到帕雷托最优解统计平均数目. 由图4可得以下几点结论:①帕雷托最优解的数目随着测试代价和延迟代价分布的变化而变化;②当测试代价或者延迟代价的分布为均匀分布时,帕雷托最优解的数目会随着代价的变化而变化;③当测试代价和延迟代价的分布为正态分布或者有界的帕雷托分布时,帕雷托最优解的数目不会随着代价的变化而变化.这是因为均匀分布会以相同的概率产生随机的整数,而正态分布会产生大量的均值附近的数值,同时,有界的帕雷托分布会产生大量小的数值和少量大的数值. 本文基于粗糙集理论中属性约简的概念,定义了多目标代价敏感约简问题,并设计了一种简单高效的算法.对UCI数据库中选取的有代表性数据集的测试结果表明,该算法能获得令人满意的帕雷托最优解集,以辅助用户优化选择方案.在以后的研究工作中,可以进一步研究更加高效的启发式算法来解决多目标代价敏感约简问题. 参考文献: [1] PAN G Y, MIN F, ZHU W. A genetic algorithm to the minimal test cost reduct problem[C]// IEEE International Conference on GrC. IEEE,2011: 539-544. [2] XU Z L, MIN F, LIU J B, ZHU W. Ant colony optimization to minimal test cost reduction[C]// IEEE International Conference on GrC.IEEE,2012: 585-590. [3] ZHAO H, MIN F, ZHU W. Test-cost-sensitive attribute reduction based on neighborhood Rough set[C]// 2011 IEEE International Conference on GrC. IEEE,2011: 802-806. [4] MIN F, ZHU W. Minimal cost attribute reduction through backtracking[C]// Proceedings of International Conference on Database Theory and Application, 258 of FGIT-DTA/BSBT, CCIS. 2011: 100-107. [5] MIN F, ZHU W. A competition strategy to cost-sensitive decision trees[C]// RSKT. 2012: 359-368. [6] DEB K, PRATAP A, AGARWAL S. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. Evolutionary Computation. IEEE Transactions on, 2002, 6 (2): 182-197. [7] LI L, CHEN H P, MIN F, et al. Attribute reduction in time-cost-sensitive decision systems through backtracking[J]. Journal of Information and Computational Science,accepted, 2013. [8] HU Q H, YU D R, LIU J F, et al. Neighborhood rough set based heterogeneous feature subset selection[J]. Information Sciences, 2008, 178 (18): 3577-3594. [9] PAWLAK Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341-356. [10] QIAN Y H, LIANG J Y, PEDRYCZ W, et al. Positive approximation: An accelerator for attribute reduction in rough set theory[J]. Artificial Intelligence, 2010, 174 (9/10): 597-618. [11] 王国胤, 于洪, 杨大春. 基于条件信息熵的决策表约简[J]. 计算机学报, 2002, 25(7): 759-766. [12] MIN F, ZHU W, ZHAO H, et al. Coser: Cost-senstive rough sets[EB/OL].(2012-01-01). http://grc.fjzs.edu.cn/~fmin/coser/.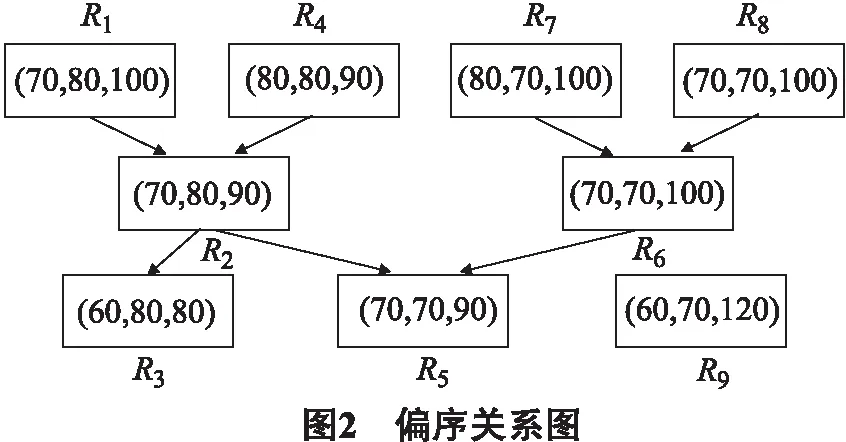
2 多目标属性约简算法
2.1 算法基本思想及具体步骤
2.2 算例
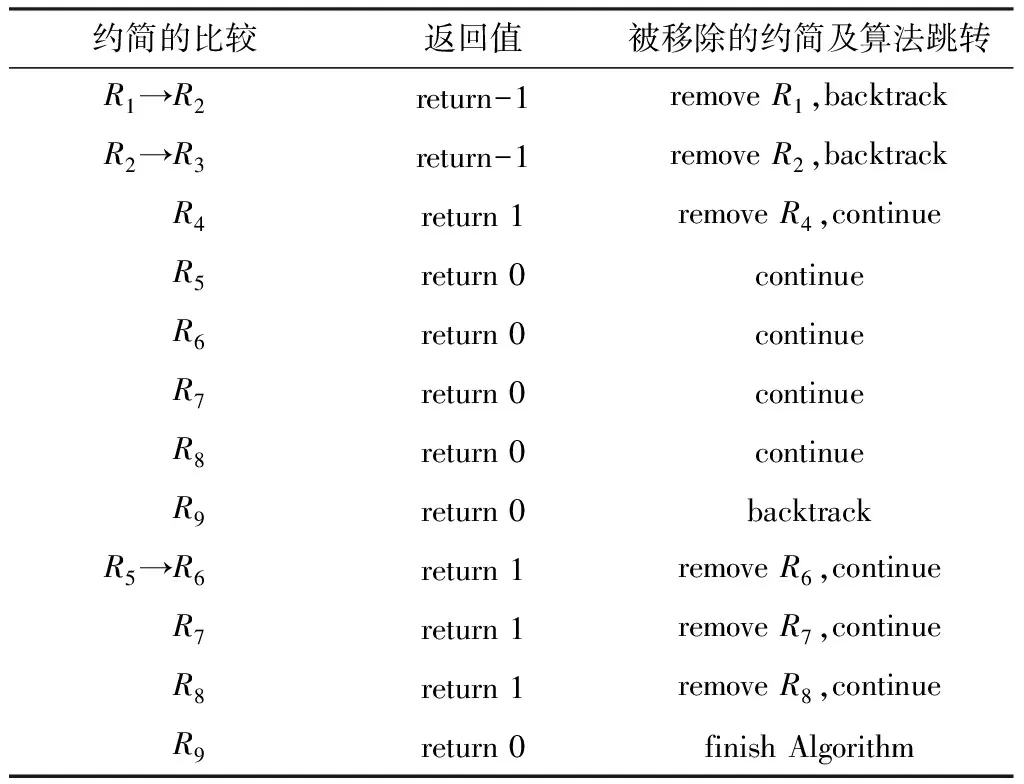
3 实验结果
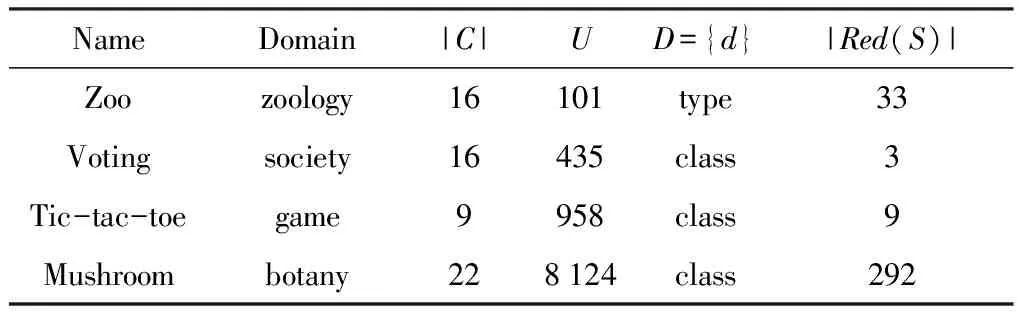
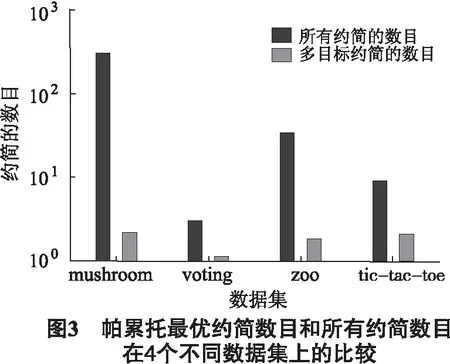
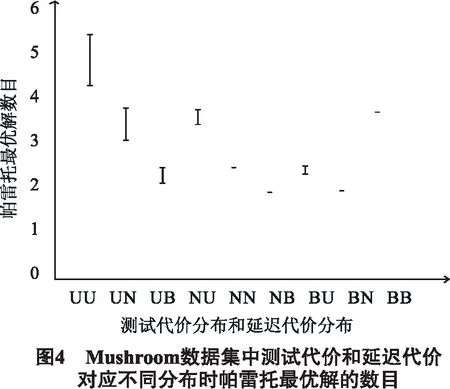
4 结语
