三维非均匀不可压缩Navier-Stokes方程弱解的存在性

朱道宇

(贵州民族大学 理学院，贵州 贵阳 550025)

考虑如下的非均匀不可压缩Navier-Stokes方程

(1)

ρ|t=0=ρ0，

(2)

u|t=0=u0.

(3)

当密度ρ为常数时，方程(1)简化为均匀不可压缩Navier-Stokes方程，也称Navier-Stokes方程．如果设ρ=1，则Navier-Stokes方程为

(4)

在文献[2-3]中，Scheffer为研究恰当弱解而给出了Navier-Stokes方程的部分正则性理论，Caffarelli等[4]对Scheffer的结果进行了改进，由此证明了对任一恰当弱解，奇异集具有一维Hausdorff零测度．恰当弱解与一般弱解的差别在于，它必须满足分布意义下的局部能量不等式：

(5)

事实上，局部能量不等式(5)可以看成是如下被Leray-Hopf弱解所满足的能量不等式的局部形式：

下面给出关于非均匀不可压缩Navier-Stokes方程的满足局部能量不等式的弱解的存在性定理.

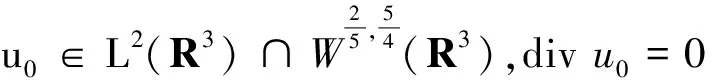
亦即不等式

对空间中任一具有紧支集的C∞函数φ≥0成立．这里的

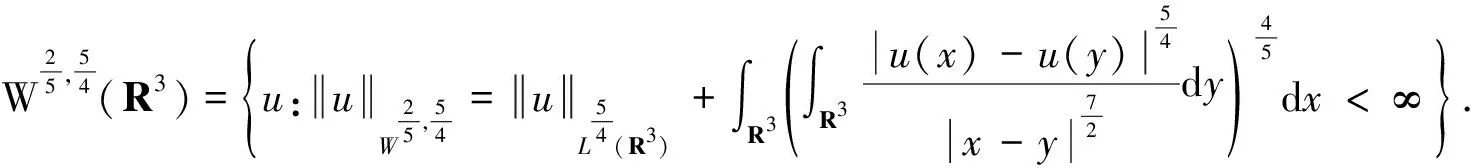
第1步 求解近似方程，构造方程(1)～(3)的近似解(ρn,un,Fn)．

由文献[1]中定理2.6知，下面的方程

(6)

具有满足初值条件

(7)

(8)

un=unωn

(9)

(10)

第2步 (ρn,un)的一致估计和收敛性，方程(1)的弱解的存在性．

由方程(6)的能量定律得

(11)

其中C与n无关．又由(10)式知ρn有一致的正下界，所以

(12)

利用Sobolev嵌入和(11)式，得

(13)

在(12)和(13)式之间作插值，得

(14)

再利用Holder不等式，可以从(9)～(11)和(14)式推出

(15)

利用文献[1]中定理2.5，存在某个函数ρ使得对任意的T>0和R>0，当n→∞时有

ρn→ρ∈C([0,T];Lp(BR))，p∈[1,+∞),

其中u满足对任意的R>0，当n→∞时有

(16)

从上面的收敛结果可知，对任意的T>0和R>0，当n→∞时有

(17)

(18)

其中的un如(9)式所定义．类似于文献[1]中关于存在性的证明，可得(ρ,u)满足(1)～(3)，因而是(1)～(3)的弱解．

第3步Fn的一致估计和收敛性．

为了得到局部能量不等式，需要对近似压力作一致估计．通常，对于不均匀Navier-Stokes方程，对任意的T>0和R>0都有

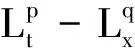
其中的C与T和n无关．

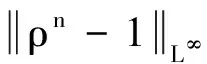
运用Sobolev嵌入，得到近似压力的一致估计为

因此Fn必存在一个弱收敛的子列，不妨仍记为Fn，即当n→∞时有

(19)

第4步 局部能量不等式．

用un分别乘以(6)式的前2个方程并相加，得到在R3×(0,T)中成立的等式：

(20)

根据收敛结果(16)～(19)式，可以推出

在(20)式中令n→∞并结合上面4式，得到如下的不等式

参考文献:

[1] LIONS P L.Mathematical topics in fluid mechanics[M]. New York:Oxford University Press, 1996.

[2] SCHEFFER V. Partial regularity of solutions to the Navier-Stokes equations[J]. Pacific J Math, 1976, 66(2): 535-552.

[3] SCHEFFER V. Hausdorff measure and the Navier-Stokes equations[J]. Communications in Mathematical Physics, 1977, 55(2): 97-112.

[4] CAFFARELLI L, KOHN R, NIRENBERG L. Partial regularity of suitable weak solutions of the Navier-Stokes equations[J]. Communications on pure and applied mathematics, 1982, 35(6): 771-831.

[5] SOLONNIKOV V A. A priori estimates for solutions of second-order equations of parabolic type[J]. Trudy Matematicheskogo Instituta im VA Steklova, 1964, 70: 133-212.

[6] SIMON J. Nonhomogeneous viscous incompressible fluids: existence of velocity, density, and pressure[J]. SIAM Journal on Mathematical Analysis, 1990, 21(5): 1093-1117.

[7] GIGA Y, SOHR H. AbstractLpestimates for the Cauchy problem with applications to the Navier-Stokes equations in exterior domains[J]. Journal of Functional Analysis, 1991, 102(1): 72-94.