包含第二类D-Nörlund数的一些计算公式

王海青

(惠州学院 数学系，广东 惠州 516007)

(1)

(2)

由(1)和 (2)可得[3,5-6]

(3)

(4)

由(1)和(3)容易得到

(5)

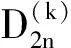
(6)

(7)

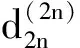
第一类和第二类D数满足下列关系[3]：

(8)

由(5)，(6)和(8)可得

(9)

(10)

(11)

(12)

(13)

第二类中心阶乘数T(n,k)由下列生成函数给出[3,9-10]：

(14)

由(14)得

(15)

T(n,0)=0(n∈N),T(n,n)=1(n∈N0)，T(n,k)=0(n+kodd),T(n,k)=0(k>n或k<0)，

这里N是正整数，且N0=N∪{0}．

由(15)得

(16)

(17)

1 主要结论

定理1 令n∈N0，则

(18)

将n=0,1,2,3代人(18)得到

定理2 令n∈N0，则

(19)

定理3 若n≥k(n,k∈N0)，则

(20)

(21)

由(16)，(17)和定理3可得

定理4 令n∈N，则

(22)

(23)

(24)

定理5 令n∈N0，则

(25)

(26)

2 定理的证明

定理1的证明由(2)和(8)可得

(27)

(27)两边对t求导得到

(28)

将k=0代人(28)有

(29)

又

得到

所以

(30)

定理2的证明由(29)和(2)可得

(31)

定理3的证明由(4)和(14)得到

所以

(32)

由(32) 和(8)可以得到 (20)．

另一方面，

所以

(33)

由(33) 和(8)可以得到 (21)，证毕．

定理4的证明由(7)可得

(34)

这里l是整数．

(35)

由(35) ，(9) ，(11)和(21)可以得到 (22)．

(36)

由(36) ，(10) ，(12)和(21)可以得到 (23)．

将k=2n,l=-1代人(34)可得

(37)

由(37) ，(11)和(20)可以得到 (24)．证毕．

定理5的证明将k=2n-1,l=-2代人(34)可得

(38)

由(38) ，(9) ，(12)和(20)可以得到 (25)．

将k=2n-2,l=-3代人(34)可得

(39)

由(39) ，(9) ，(13)和(20)可以得到 (26)．证毕．

参考文献:

[1] HOWARD F T.Congruences and recurrences for Bernoulli numbers of higher order[J]．Fibonacci Quart，1994,32:316-328．

[3] LIU G D．The D numbers and the central factorial numbers[J]．Publ Math Debrecen，2011,79(1/2):41-53．

[4] NÖRLUND N E．Vorlesungenüber Differenzenrechnung[M]．New York: Chelsea Publishing Company，1954．

[5] LIU G D．Some computational formulas for D-Nörlund numbers[J]．Abstr Appl Anal，2009, Art.ID 430452，7pp．

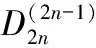
[7] LIU G D，SRIVASTAVA H M, WANG H Q．Some formulas for a family of numbers analogous to the higher-order Bernoulli numbers[J]．Journal of Integer Sequences，2014，(17)，Article 14.4.6．

[8] 王海青．包含D-Nörlund数的一些恒等式[J]．纺织高校基础科学学报，2014，27(1)：32-37.

[9] LIU G D．On congruences of Euler numbers modulo powers of two[J]．Journal of Number Theory，2008,128(12):3063-3071．

[10] RIORDAN J．Combinatorial Identities[M]．New York: Wiley,1968．