脉动风荷载时程数值模拟研究①

□□ ，小兵，

(广东理工职业学院，广东 广州 510091)

引言

风荷载是结构设计时所需考虑的一类重要的随机动力荷载。与地震作用相比，高层、超高层建筑、高耸结构、大跨度结构等在风荷载作用下的效应，对结构的安全性和适用性甚至起着决定性的影响。在结构设计计算考虑风荷载时，除了在平均风作用下对建筑结构进行静力计算外，有时还需对脉动风荷载下建筑结构的动力响应进行分析[1]。对于重要的结构，通常采用风洞试验的方法来测试其动力响应，但风洞试验方法耗时耗资巨大，目前尚无法在工程设计分析领域中普遍使用。而通过计算机模拟脉动风荷载，可以很好地帮助工程人员掌握实际工程结构的风振特性。事实上，考虑到在实际的大气边界层紊流风场中，脉动风速不仅是时间的函数，而且随空间位置而变化，是一个随机场，数值模拟方法反而比实际记录更具有代表性，因而在实际工程中被广泛使用[2-6]。

1 风场的基本特性

大气中气流的运动形成风。根据大量的风场实测资料可知，在风的顺风向时程曲线中包含脉动风和平均风两部分。平均风周期通常在10 min以上，对建筑结构的作用可按静力考虑，而脉动风周期通常只有几分之一秒，且其速度和运动方向在时空上随机，会引起建筑结构的随机振动响应。通常用功率谱和相关函数这两个函数来描述脉动风。

1.1 常用风速功率谱

脉动风的风速功率谱主要反映脉动风中各种频率成分对应的能量分布规律。按方向可分为水平脉动风速功率谱和垂直脉动风速功率谱，目前使用最广泛的是水平风速功率谱，其中Davenport谱[7]、Harris谱[8]不考虑湍流积分尺度随高度的变化情况，而Simiu谱[8]、Hino谱[9]、Kaimal谱[8]等考虑了近地表层不同高度时湍流积分尺度的变化。

上述各种常用水平风速谱的表达式见(1)式至(11)式，其中Davenport谱也是GB 50009—2012《建筑结构荷载规范》[10]采用的水平脉动风谱。

Davenport谱：

(1)

(2)

Harris谱：

(3)

(4)

Simiu谱：

(5)

(6)

当c>0.2时，取：

(7)

Hino谱：

(8)

(9)

Kaimal谱：

(10)

(11)

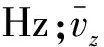
1.2 脉动风相关性

在紊流风场环境中，各点之间的风速大小及风向并不完全一致，甚至是完全无关的。脉动风在不同时间和空间上的相关程度，在时域上采用相关函数、在频域上采用相干函数来描述。

相关函数分为自相关函数Rxx(τ)和互相关函数Rxz(τ)。为了更直观了解风场各点之间相关性的大小，引入自相关系数ρxx(τ)和互相相关系数ρxz(τ)：

(12)

(13)

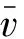
在频域上采用相干函数Coh(r,f)来表示空间点之间的相关程度，对于高层建筑那样需要同时考虑高度和宽度方向的情况，Davenport A G曾给出Coh(r,f)指数形式的经验公式[11]：

Coh(r,f)=Rxz(x1,x2,z1,z2,f)=e-c

(14)

(15)

2 脉动风时程数值模拟方法

多年以来，众多学者针对前述脉动风速功率谱，从不同的角度用随机过程方法模拟脉动风荷载时程，且满足了样本采集上的统计特征，在实际的工程应用中被广泛采用。脉动风荷载的模拟方法大体上可分为两类，即线性滤波法和谐波叠加法。线性滤波法是基于线性滤波技术的一种方法，如自回归法(AR)、滑动平均法(MA)和滑动自回归平均法(ARMA)；谐波叠加法是基于谱分解和三角级数叠加求和来模拟脉动风时程，如常数波叠加法(CAWS)和加权波叠加法(WAWS)。

2.1 线性滤波法

线性滤波法也称为白噪声滤波法或时间系列法，其基本思想是将均值为零的白噪声随机序列通过滤波器，使其输出具有指定谱特征的随机过程。

若采用线性滤波法的ARMA技术，在白噪声w(f)激励下，滑动自回归平均模型的输出为x(f)，则模型输入及输出关系的时域表达可写成[12]：

(16)

式中：G为系统增益；ai及bi为模型待定系数。当ai=0时，就成了MA模型；当bi=0时，就是AR模型。

2.2 谐波叠加法[12]

谐波叠加法也称为频谱表示法，这种方法算法简单直观，数学基础严密，其基本思想是采用以离散谱逼近目标随机过程的随机模型的一种离散化数值模拟方法。

如采用WAWS方法模拟多个相关脉动风速时程，考虑一组n维零均值平稳随机过程：

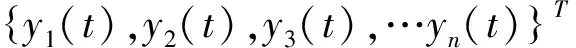
(17)

该随机过程的互谱密度函数矩阵为：

(18)

式中：Sjj(f)为自谱密度函数；Sjk(f)为互谱密度函数(j≠k)，且j,k=1,2,3…n。

Sjk(f)的表达式为复数形式：

(19)

式中：ch(f)为相干函数，其具体计算公式见(14)式和(15)式；φ(f)为相位角。

φ(f)的计算公式为：

(20)

显然，互谱密度矩阵S(f)是一个对称矩阵，将其进行cholesky分解：

S(f)=H(f)·H*(f)

(21)

其中H(f)为下三角矩阵，H*(f)是H(f)的共轭转置矩阵，由于S(f)通常情况下为复矩阵，且不一定正定，因此，H(f)通常也是复矩阵，其对角元素为实数，非对角元素为复数，H(f)的矩阵形式如下：

(22)

H(f)中的元素具有如下关系：

(23)

式中：Im[·]和Re[·]分别为Hjk(f)的虚部和实部。

根据Shinozuka理论，(17)式所表示的随机过程向量y(t)的样本可由(24)式来模拟：

(j=1,2,…,n) (24)

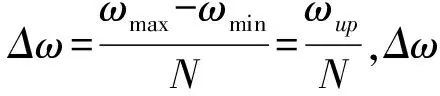
3 结语

脉动风荷载时程的模拟是建筑结构风致振动控制仿真分析中非常基础且重要的一步，多年以来，国内外众多学者在相关方面做了大量的工作。本文介绍了近地表层风场的基本特性，阐述了脉动风场模拟时的脉动风速功率谱和空间相关函数这两个特征参数。对实际工程应用过程中的两类脉动风时程数值模拟方法，即线性滤波法和谐波叠加法的原理进行了介绍，特别是对谐波叠加法模拟脉动风速时程的数学形成过程进行了较深入的研究。

参考文献：

[1] JGJ 3—2010，高层建筑混凝土结构技术规程[S].北京：中国建筑工业出版社，2011.

[2] Paola M D.Digital simulation of wind field velocity[J].JournalofWindEngineeringandIndustrialAerodynamics，1998，23(2)：74-76.

[3] Deodatis G.Simulation of ergodic multivariate stochasticprocess[J].JournalofEngineeringMechanics,ASCE，1996,122(3)：778-787.

[4] 罗俊杰，韩大建.大跨度结构随机脉动风场的快速模拟方法[J].工程力学，2008,25(3)：96-101.

[5] 陈俊儒，吕西林.上海中心大厦脉动风荷载模拟研究[J].力学季刊，2010，31(1)：92-101.

[6] 汪大洋，袁玲，周云.基于改进线性滤波法的某超高层建筑风振反应分析[J].广州大学学报：自然科学版，2013,12(3)：21-24.

[7] Simiu E，Scanlan R H.风对结构的作用——风工程导论[M].刘尚培译.上海：同济大学出版社，1992.

[8] Simiu E.Wind spectra and dynamic along wind response[J].JournaloftheStructuralDivision,ASCE，1974,100(9)：1897-1910.

[9] 黄本才.随高度变化的脉动风速谱及风振计算[A].力学与应用论文集[C].上海：同济大学出版社，1992.

[10] GB 50009—2012，建筑结构荷载规范[S].北京：中国建筑工业出版社，2012.

[11] 黄本才，汪丛军.结构抗风分析原理及应用[M].上海：同济大学出版社，2008.

[12] 陈小兵.基于能量的高层建筑结构风振控制设计方法研究[D].广州：广州大学，2010.