一种改进的共反射面元叠加方法

邓金华,李 栋,王立歆,徐兆涛

(1.中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营257022;2.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

从20世纪80年代末开始,地球物理学家们逐步提出了一些不依赖于宏观速度模型的多参数叠加方法,如延迟双曲线叠加技术、同胚成像(Homeomorphic Imaging,HI)技术、共聚焦点(Common Focus Point,CFP)成像技术、多次聚焦(Multifocusing,MF)成像技术[1-3]以及共反射面元(CRS)叠加技术等,其中以德国卡尔斯鲁厄大学波反演技术(Wave Inversion Technology,WIT)课题组提出的共反射面元叠加方法最具代表性[4-10]。CRS叠加算子由旁轴射线理论推导而来,考虑地下反射层的局部地质特征,叠加过程中将目标反射点邻域内共反射面元上所有反射点的信息进行校正和叠加,显著提高了地震资料品质。

初始CRS叠加方法假定中心射线为法向射线,且仅适用于二维水平地表地震记录的处理,称为二维零偏移距(ZO) CRS叠加[4-6]。Zhang等[7]、Bergler等[8]将ZO CRS叠加方法扩展到三维地震资料处理,取得了较好效果。Boelsen[9]推导了适用于起伏地表的ZO CRS叠加算子,证明基于光滑起伏地表假设推导的简化叠加算子更适合处理实际地震资料。Baykulov等[10]利用ZO CRS叠加属性参数进行部分叠加,得到的叠前共中心点道集品质明显提高,有利于后续常规处理。Zhang等[11-12],Bergler等[13]基于ZO CRS叠加概念发展了共偏移距(Common-Offset,CO)CRS叠加技术,其算子以任意非零偏移距射线为中心射线。Bergler等[14]利用CO CRS叠加方法处理转换波数据,通过近地表的纵、横波速度和出射角度信息将PP波和PS转换波进行分离。Boelsen[15-17]将CO CRS叠加算子推广到起伏地表情况,对其进行简单变形就可用于海底地震(Ocean Bottom Seismic,OBS),VSP,逆VSP,井间地震等数据处理,具有广泛的适用性。

国内地球物理学者也对共反射面元叠加技术的理论推导和算法实现进行了研究，并在许多探区有成功的应用实例。韩立国等[18]提出CRS与CMP联合叠加成像方法,简化CRS叠加实现过程,提高其计算效率。李振春等[19]针对CRS叠加的运算效率和成像精度问题,推导了参数多级优化的CRS叠加方法。杨锴等[20]提出输出道成像方式的CRS叠加,该方法能够保证大炮检距反射信息的成像精度,且计算效率较高。Sun等[21]在复杂地表CRS叠加过程中引入模拟退火算法,有效解决了波场三参数耦合带来的参数搜索和优化难题。吴小羊等[22]推导出CRS最优叠加孔径,使地震信号能量达到最佳,同时提高了地震资料的信噪比和分辨率。

CRS叠加算子涉及多个叠加参数,为提高计算效率,具体实现时往往采用多级优化策略,然而常用的参数搜索算法并未考虑叠加剖面中反射同相轴相交,即同一零偏移距位置处存在多个不同倾角的同相轴的情况。我们针对实现过程中的全局最优化问题改进参数搜索策略,通过引入相干阈值方法求得目标成像点处的全局和局部最大值,有效解决了零偏移距剖面中多个同相轴相交的问题。

1 方法原理

1.1 CRS叠加算子及常规实现策略

基于旁轴射线理论和二阶泰勒展开,推导出二维情况下共反射面元的旅行时近似公式,在以中心点xm和半偏移距h建立的坐标系中,其双曲型叠加算子为[4]

(1)

式中:t为旁轴射线的双程旅行时;t0为中心射线的双程旅行时;Δxm为旁轴射线与中心射线在中心点处的偏离距离;h为旁轴射线的半偏移距;v0为近地表处的地震波速度;β为中心射线在地表处的出射角;RN,RNIP分别为法向波和法向入射点波的波前曲率半径。三参数(β,RN,RNIP)代表运动学波场属性,刻画了二维地下介质中反射界面的局部构造特征,即反射段的位置、倾向和曲率,称为CRS叠加算子参数。

高效解决三参数优化问题的途径是将其分解为3个单参数分别进行优化,由叠前地震数据的子集(如CMP道集,ZO剖面)得到CRS叠加算子的简化式。在CMP道集中,叠加算子简化为

(2)

其中,组合参数q为

(3)

在ZO剖面中(h=0),叠加算子简化为

(4)

观察(2)式和(4)可见,叠加算子中未知参数的数量降为1～2个,这样就可以将CRS叠加分成几步来做,快速准确地确定三参数对的初始值。将得到的叠加参数值作为优化算法的起点,应用到原始多次覆盖地震数据中,利用方程(1)所示的双曲叠加算子得到最终CRS叠加剖面及波场属性剖面。我们所采用的优化算法为Nelder等[23]提出的灵活多面体搜索方法。

以上步骤可总结为流程图形式,如图1所示。

1.2 改进的参数搜索策略

传统的参数搜索策略与CMP叠加和倾斜叠加等常规地震处理方法联系紧密,在CRS叠加处理流程中借鉴这些较为成熟的方法,可大幅度提高CRS叠加的计算效率。图1所示常规CRS叠加算法虽然实用,但存在一个无法避免的问题:由公式(2)得知,自动CMP叠加算子仅依赖于出射角度β和曲率半径RNIP的组合参数,并且与β值的正负没有关系,所以该算法无法处理同相轴相交的情况。这意味着,在同相轴相交的情况下,任何一个同相轴的参数都无法通过该算法确定,因为所有做出贡献的反射同相轴均会对组合参数的扫描造成影响。因此,研究一种既能克服常规搜索算法的缺陷，又能保持较高计算效率的参数搜索策略非常必要。

图1 常规CRS叠加参数搜索简易流程

在共反射面元叠加过程中，无法利用CMP道集处理同相轴相交的情况,因为CMP道集中反射同相轴的曲率(即参数RN)没有贡献,并且存在倾角(即参数β)的数值大致相等而符号相反的情况。而ZO剖面能处理同相轴相交的情况,不过在实际野外采集中无法得到零偏移距道集,所以需要对常规的参数搜索策略进行改进。需要注意的是,若CMP叠加剖面中同相轴的倾角或曲率不同,肯定会在相邻道上出现分离,所以即便CMP叠加过程无法考虑相交倾角/曲率的情况,其剖面仍适于进行后续的处理及分析。倾角相交情况意味着有不同的出射角β(i)值(索引i表示多个同相轴),可以通过ZO叠加过程中得到的附加相干最大值来处理该情况。常规倾角校正未考虑具有不同倾角的所有有贡献同相轴的信息,而CRS叠加方法则需要对每个检测出的同相轴,也就是对每个ZO位置处明确有贡献的同相轴(基于CMP叠加剖面利用相干分析得到)确定其参数。为检测有效同相轴对应的全局和局部最大值,我们引入相干阈值方法并设定以下判别标准。

1) 全局最大相干值必须大于所设定阈值,否则舍弃搜索出的所有局部最大值,避免在不含真实同相轴的噪声区域进行运算,以节省计算成本。

2) 局部最大值必须大于与全局最大值有关的阈值,其反映了真实反射同相轴在相同旅行时和叠加孔径条件下应得到类似相干值的假设。

3) 为防止因噪声的起伏而对同一个相干峰值进行多次检测,相干最大值之间需要明显地分开。

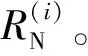
根据以上原理及分析,改进的共反射面元叠加流程如图2所示。

图2 改进的CRS叠加参数搜索策略

2 模型数据试算和实际资料处理

2.1 Sigsbee 2a模型数据试算

首先对具有复杂地质构造特征的Sigsbee 2a模型数据进行叠加处理试验,其正演记录共500炮,单炮最大道数为348道,炮间距为45.72m,道间距为22.86m,数据采样率为8ms,记录长度为12s,偏移距范围为0～7932.42m。图3a为利用改进的参数搜索策略得到的CRS叠加剖面,与传统的CRS叠加剖面相比,整体上难以发现两者差别(故未给出传统的CRS叠加剖面)。图3b和图3c 分别为传统的CRS叠加剖面和改进的CRS叠加剖面局部放大图(图3a中红框所示位置),可以看出传统的CRS叠加方法由于只考虑主同相轴,大部分强弯曲同相轴被压制,而改进的CRS叠加方法考虑了同一位置处存在多个同相轴相交的情况,模拟的ZO剖面更加真实可靠,图中陡同相轴被证明为绕射同相轴。

对于同一ZO位置有贡献同相轴多于一个的情况,可以确定几组波场属性,利用这些属性可以验证陡相交同相轴的本质。图3d为主同相轴的出射角,图3e为局部最大值对应的次同相轴的出射角,对比可见,不同的贡献同相轴可通过其不同的出射角加以区分,并且绕射波在两个剖面中均有显示。对于绕射波,其对应的法向波和法向入射点波重合,即参数RN和RNIP相等,图3f和图3g分别为主、次同相轴的参数RN与RNIP的比率,该比率沿陡同相轴的值接近于1,证实其为绕射同相轴,验证了相交同相轴情况下波场属性的一致性。

2.2 实际地震资料处理

利用实际地震资料验证改进的CRS叠加方法的实用性。该地震数据共310炮,单炮最大道数为110道,道间距为40m,数据的采样率为2ms,采样点数为2500,偏移距范围为-2320～2360m。图4a为利用常规CMP叠加方法得到的剖面,图4b 至图4c分别为利用传统的CRS叠加方法和改进的CRS叠加方法得到的叠加剖面,可以看出,由于CRS叠加孔径增加了参与叠加的道数,所以图4b和图4c所示叠加剖面的信噪比比图4a显著提高,同相轴的连续性得到增强,剖面整体品质得到明显改善。对比图4b和图4c可以看出,同相轴相交的问题在传统CRS叠加剖面中并未得到解决,同一成像位置处只保留了相干值最大的同相轴,而其它同相轴则被压制;改进的CRS叠加方法考虑了同相轴相交的情况,模拟的ZO剖面同相轴更加清晰自然,符合地下真实的构造情况。图5a 和图5b分别为传统的CRS叠加剖面和改进的CRS叠加剖面中红框所示区域的局部放大图,通过对比可以更加清楚地看到,改进的CRS叠加剖面中同相轴相交位置处,不仅能量较强的反射同相轴比较清晰,能量较弱的绕射信息也得到较好的保护,显示的信息更加真实可靠。

图3 Sigsbee 2a模型数据叠加结果a 改进的CRS叠加剖面; b 传统的CRS叠加剖面局部放大; c 改进的CRS叠加剖面局部放大; d 主同相轴出射角度; e 次同相轴出射角度; f 主同相轴参数RN/RNIP; g 次同相轴参数RN/RNIP

图4 实际地震资料处理结果a 常规CMP叠加剖面; b 传统的CRS叠加剖面; c 改进的CRS叠加剖面

图5 实际地震资料处理结果局部放大 a 传统的CRS叠加剖面; b 改进的CRS叠加剖面

3 结束语

本文针对传统的CRS叠加方法的局限性,改进参数搜索步骤,通过引入相干阈值的方法确定ZO位置处目标点的全局和局部最大值,从而有效地处理同一ZO位置处存在多个有贡献同相轴的情况。改进的CRS叠加方法考虑了同相轴相交的情况,模拟的ZO剖面更加真实可靠,成像效果更好。

参 考 文 献

[1] Gelchinsky B,Berkovitch A,Keydar S.Multifocusing homeomorphic imaging,part1:basic concepts and formulas[J].Journal of Applied Geophysics,1999,42(3/4):229-242

[2] Gelchinsky B,Berkovitch A,Keydar S.Multifocusing homeomorphic imaging,part2:multifold data set and multifocusing[J].Journal of Applied Geophysics,1999,42(3/4):243-260

[3] Berkovitch A,Belfer I,Hassin Y,et al.Diffraction imaging by multifocusing[J].Geophysics,2009,74(6):WCA75-WCA81

[4] Müller T.The common reflection surface stack method:seismic imaging without explicit knowledge of the velocity model[D].Germany:Geophysical Institute,University of Karlsruhe,1999

[5] Jäger R,Mann J,Höcht G,et al.Common-reflection-surface stack:imaging and attributes[J].Geophysics,2001,66(1):97-109

[6] Mann J.Extensions and applications of the common-reflection-surface stack method[D].Germany:Geophysical Institute,University of Karlsruhe,2002

[7] Zhang Y,Hocht G,Hubral P.2D and 3D ZO CRS stack for a complex top-surface topography[J].64thEAGE Conference & Exibition,2002,166

[8] Bergler S,Hubral P,Marchetti P,et al.3D common reflection surface stack and kinematic wavefield attributes[J].The Leading Edge,2002,21(10):1010-1015

[9] Boelsen T.The common-reflection-surface stack for arbitrary acquisition geometrics and multi-component data-theory and application[D].Germany:University of Karlsruhe,2005

[10] Baykulov M,Gajewski D.Prestack seismic data enhancement with partial common-reflection-surface (CRS) stack[J].Geophysics,2009,74(3):49-58

[11] Zhang Y H,Bergler S,Hubral P.Common-reflection-surface (CRS) stack for common offset[J].Geophysical Prospecting,2001,49(6):709-718

[12] Zhang Y,Bergler S,Hubral P.Common-reflection-surface stack for common offset:theoretical aspects[J].63rdEAGE Conference & Exibition,2001,78

[13] Bergler S,Höcht G,Zhang Y,et al.Common-reflection-surface stack for common offset:practical aspects[J].63rdEAGE Conference & Exibition,2001,76

[14] Bergler S,Duveneck E,Hocht G,et al.Common reflection surface stack for converted waves[J].Studia Geophysica et Geodaetica,2002,46(2):165-175

[15] Boelsen T.The common-reflection-surface stack for arbitrary acquisition geometrics and multi-component data-theory and application[D].Germany:University of Karlsruhe,2005

[16] Boelsen T.2D CO CRS for OBS and VSP data and arbitrary top-surface topography[J].67thEAGE Conference & Exibition,2005,181

[17] Boelsen T.2D CO CRS for multi-component seismic reflection data[J].67thEAGE Conference & Exibition,2005,63

[18] 韩立国,孙建国,何樵登,等.共反射面与共中心点联合叠加成像[J].石油物探,2003,42(1):25-28

Han L G,Sun J G,He Q D,et al.Imaging by joint CRS and CMP stacking[J].Geophysical Prospecting for Petroleum,2003,42(1):25-28

[19] 李振春,姚云霞,马在田,等.基于参数多级优化的共反射面元叠加方法及其应用[J].石油地球物理勘探,2003,38(2):156-161

Li Z C,Yao Y X,Ma Z T,et al.Common reflection surface method based on multi-level optimization of parameters and its application[J].Oil Geophysical Prospecting,2003,38(2):156-161

[20] 杨锴,许士勇,王华忠,等.倾角分解共反射面元叠加方法[J].地球物理学报,2005,48(5):1148-1155

Yang K,Xu S Y,Wang H Z,et al.A method of dip decomposition common reflection surface stack[J].Chinese Journal of Geophysics,2005,48(5):1148-1155

[21] Sun X D,Li Z C.Common reflection surface stack using dip decomposition for rugged surface topography[J].Applied Geophysics,2007,4(1):45-50

[22] 吴小羊,刘天佑,魏伟,等.二维菲涅耳带共反射面元叠加方法研究[J].地球物理学报,2008,51(6):1892-1898

Wu X Y,Liu T Y,Wei W,et al.Two dimensional common reflection surface stack based on the Fresnel zone[J].Chinese Journal of Geophysics,2008,51(6):1892-1898

[23] Nelder A,Mead R.A simplex method for function minimization[J].The Computer Journal,1965,8(4):308-313