斑状饱和介质的粘弹特性表征与地震波模拟
2014-03-25李晓波董良国
李晓波,董良国
(同济大学海洋地质国家重点实验室,上海200092)
斑状饱和是沉积岩中重要的流体赋存形式,在近地表的岩石中以气、水斑状分布为主,在深部储集层中还存在油或其它烃类的分布形式[1]。Cadoret等通过CT技术呈现了石灰岩中厘米尺度的气、水斑块状分布特征[2];Quintal等也通过CT技术证明了砂岩中存在气、油斑状分布的客观事实[3]。地震波在斑状饱和介质中传播时会发生较强能量衰减。White(1975)首次考虑介观尺度(mesoscale,远大于孔隙尺寸且远小于地震波波长)斑状饱和介质,成功预测了地震勘探频带(1~1000Hz)内的地震波强衰减和速度频散特征[4]。理论分析[5-8]和实验室测量[9]均表明,介观尺度波致流体流动(wave-induced fluid flow)是导致斑状饱和介质中地震波本征衰减的主要原因。斑状饱和介质中的地震波传播理论考虑了地震波衰减的物理机制,且衰减与储层参数之间关系密切[10-11],因此研究斑状饱和介质中的地震波传播特征对于储层预测非常重要。利用孔隙弹性理论[12-14]可以研究斑状饱和介质中的地震波传播特征[15-16],基于该理论的数值模拟技术常被用于模拟斑状饱和介质中的地震波传播[17-18],并准确求出地震勘探频带内的地震波强衰减和速度频散特征[1,19-21]。然而,描述斑状饱和介质所需的储层参数比较多,并且需要采用厘米甚至毫米级的空间网格才能描述介观尺度的非均质特征[19,22],导致地震波数值模拟中的计算量超过常规弹性波正演的千万倍,使得基于斑状饱和介质的地震波传播数值模拟技术无法真正应用于实际。为此,一些学者考虑用等效粘弹模型定量表征斑状饱和介质中的地震波衰减和速度频散特征[10,23-25]。
斑状饱和介质中的地震波衰减和速度频散可由低频极限(弛豫状态)模量M0以及高频极限(非弛豫状态)模量M∞和特征频率fc(衰减峰值发生的频率)3个重要参数描述[26],标准线性体(SLS)[26-27]则是结合这3个参数的一个理想粘弹模型。该模型虽然未特别强调地震波衰减发生的物理机制[26],但可以预测出斑状饱和介质中的地震波衰减和速度频散等粘弹性质,而且使描述孔隙介质的参数大幅度减少,便于我们通过数值模拟来研究斑状饱和介质中的地震波传播规律,极大地降低了数值计算量,因而具有更强的实用性。Sidler等[28]首次对比了基于斑状饱和与粘滞弹性理论模拟得到的地震波记录。我们首先将复杂的储层参数简化为高、低频极限弹性模量及特征频率3个变量,采用SLS模型定量表征斑状饱和介质中的地震波衰减及速度频散特征,进而通过数值模拟分析孔隙度和含气饱和度的变化对斑状饱和介质中地震波振幅和相位特征的影响。
1 斑状饱和与粘滞弹性理论简介
1.1 斑状饱和理论
一般情况下,孔隙储层的储集空间中总有多种流体(如气、水、油等)同时充填。斑状饱和介质考虑两种流体同时充填,采用岩石弹性模量、孔隙度、渗透率、流体粘滞系数、流体饱和度、密度等储层参数来定量刻画储层单元的特征。考虑一斑状饱和的孔隙储层岩石单元,其骨架的体积模量为Kdry,剪切模量为μdry,孔隙度为φ。组成岩石骨架的固体颗粒的体积模量为Ks,孔隙中充填气、水两种流体,其体积模量分别为Kg和Kw,含气饱和度为Sg。在斑状饱和介质中,流体分布是非均质的,存在一个临界弛豫尺度Lc,与孔隙流体的体积模量Kf和粘滞系数ηf以及岩石骨架的孔隙度φ和渗透率κ共同决定了地震波衰减发生的特征频率fc[29]:
(1)
当频率足够低时,弛豫尺度无限大,由波动诱发的孔隙压力在整个孔隙空间中可以有足够的时间达到平衡,此时岩石的体积模量可由Gassmann理论[30]准确计算得到,即
(2)
式中:α=1-Kdry/Ks;M=Ks/(α-φ+φKs/Kf)。此时Kf为极限低频条件下的流体体积模量,可由有效流体模型预测得到[26]
(3)
当频率无限高时,弛豫尺度无限小,由波动引起的孔隙压力在含不同流体的区域无法达到平衡,含水和含气的岩石具有不同的体积模量K(Kw)和K(Kg)(可用Gassmann理论作局部性描述),但是整个岩石的剪切模量不受流体影响,即μ=μdry。因此基于Hill平均[31]可准确求取高频条件下斑状饱和岩石的有效体积模量:
(4)
根据(5)式和(6)式即可求得斑状饱和模型中P波模量的高、低频极限:
1.2 粘弹介质模型
粘弹介质模型常被用于描述复杂介质中的地震波传播。SLS模型(图1)是一个较理想的线性粘弹性体,由一个弹性单元与一个粘性单元并联后,再与一个弹性单元串联组成,其应力-应变关系为[26]
(7)
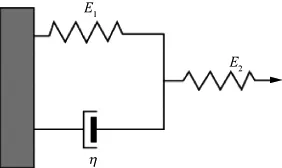
图1 三元件标准线性粘弹性体模型[26]
当频率趋近于0和趋近于无穷大时,根据(8)式可以得到SLS模型复模量的极限:
M∞=E2ω→∞
(10)
M0和M∞都是与频率无关的实数,因此,在无限高频和无限低频条件下SLS模型呈现为弹性性质。复模量也可以简单地用两个极限和特征频率来表示[26]:
(11)
其中,ωc为特征圆频率,即
(12)
1.3 粘弹性表征
逆品质因子Q-1常被用于定量表征介质的粘弹性质,具有多种表达形式,其中复模量的虚部与实部之比是一种精确的表达方式[26]:
(13)
速度频散常伴随地震波衰减发生,根据复弹性模量和介质密度ρ即可得到不同频率条件下的P波传播速度:
(14)
为了分析SLS模型对斑状饱和储层单元粘滞性的表征能力,考虑一斑状饱和岩石,其储层参数如表1所示(根据实验室测量结果[32]计算所得),孔隙度为20%,含气饱和度为10%。其中每个含气斑块的储层岩石单元为一边长1m的立方体,此时含气斑块的直径约为0.58m(与介观尺度的定义一致),特征频率约为32Hz。

表1 斑状饱和储层单元的物性参数
基于斑状饱和介质模型和SLS模型,从理论上预测了表1中孔隙介质的地震波衰减和速度频散特征,见图2。图2中蓝色曲线表示SLS模型的预测结果,红色曲线表示斑状饱和理论[33]的预测结果。可以看出,地震波衰减在低频段随着频率增加而增加,在特征频率达到最大;在高频段又随着频率的增加逐渐降低。P波速度的低频极限约为3250m/s。随着频率的增加,P波速度逐渐增大,在特征频率附近P波速度增加最快,在高频段又逐渐趋近于3470m/s。基于SLS模型预测的地震波最大衰减略高于斑状饱和理论的预测结果(图2a),P波速度更快地达到高频极限(图2b),但二者的总体特征表现出了很强的一致性,说明至少从纵波的衰减和频散角度看,利用SLS粘弹模型可以较好地表征比较复杂的斑状饱和介质模型。

图2 斑状饱和介质(表1所示参数)中纵波衰减(a)和速度频散(b)理论曲线
2 基于SLS模型的斑状饱和介质中地震波传播模拟
从上述分析可知,SLS模型可以有效地表征斑状饱和介质的粘弹(地震波衰减和速度频散)特征。与斑状饱和介质模型相比,SLS模型描述介质的粘弹性质所需要的参数大幅度减少。基于SLS模型的波动方程易于数值求解,极大地降低了地震波传播数值模拟的计算量,更便于研究孔隙介质的粘弹特性。为此,本文在建立斑状饱和介质模型与SLS模型在表征孔隙介质的粘弹特性关系的基础上,采用基于SLS模型的地震波传播数值模拟方法,研究斑状饱和介质中的地震波传播特征。
对于表1中的均匀斑状饱和介质模型,为了得到地震勘探频带内所有频率成份的地震波信息,数值模拟试验中选取宽频Ricker子波[34]作为子波函
数,即
(15)
两个主频分别为f0=50Hz,f1=500Hz,子波延迟时t0=20ms。时间、空间采样间隔分别采用0.05ms和1m;震源点(图3中红色五角星标注)坐标为(0,0),模型深度为200m。
采用VSP观测系统,记录201个不同深度位置(图3中黄色五边形标注)接收的地震记录。由图3可见,随着传播距离的增加,地震波振幅快速减小,并且发生了严重的物理频散现象,地震波波形变化明显。从对应的振幅谱(图4)上可以看出,随着传播距离的增大,地震波能量发生了较强的衰减,且主要能量的频带快速向低频移动。
为了进一步验证通过SLS模型模拟斑状饱和介质中地震波传播思路的正确性,我们利用基于SLS模型模拟的地震波记录求取地震波衰减和速度频散曲线,并将其与斑状饱和介质理论的预测结果进行对比(图5)。由图5可以看出,除少数频率成分的计算结果存在较小的偏差外,根据SLS粘弹模型模拟的地震波记录可以较好地预测出斑状饱和介质中整个地震勘探频带的P波逆品质因子和P波传播速度随频率的变化特征。因此,根据SLS模型模拟的地震记录可较好地计算斑状饱和介质中的地震波衰减和速度频散特征,为研究斑状饱和介质中地震波场特征与储层参数的定量关系提供了一种简单、快速的数值分析工具。
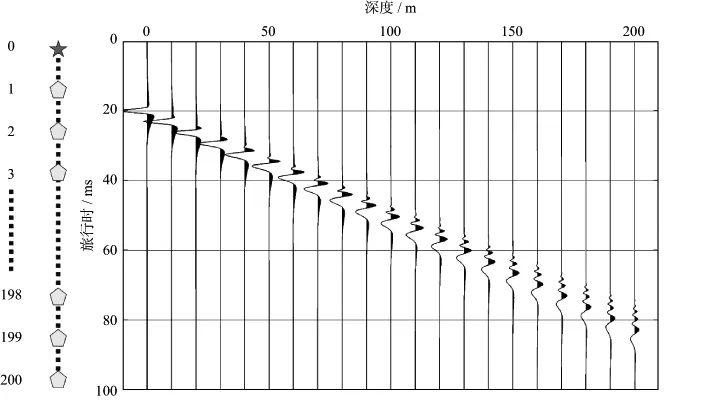
图3 一维均匀斑状饱和介质中VSP观测方式及模拟记录

图4 零偏VSP模拟记录(压力场)的频谱
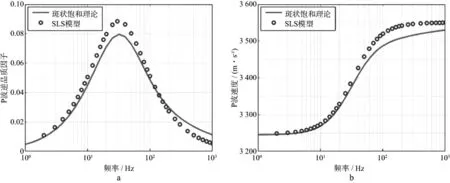
图5 斑状饱和介质(表1所示参数)中纵波衰减(a)和速度频散(b)理论曲线(蓝色散点线为基于SLS模型模拟的地震记录的数值计算结果,红色曲线为斑状饱和理论的预测结果)
3 储层参数对斑状饱和介质中地震波场特征的影响分析
前人对斑状饱和介质中的地震波衰减和速度频散特征研究结果表明,含气饱和度和孔隙度是影响斑状饱和介质中地震波衰减和速度频散的两个重要储层参数[10-11],也是重要的储层表征参数,因此,研究含气饱和度和孔隙度对地震记录的影响显得尤为重要。但是,采用斑状饱和介质模型进行地震波模拟所需参数多,计算量异常庞大,为此,我们在定量表征斑状饱和介质模型粘弹效应的基础上,采用基于SLS模型的地震波数值模拟方法,研究斑状饱和介质中含气饱和度和孔隙度对地震波传播特征的影响。
3.1 含气饱和度的影响
根据表1所示储层参数建立均匀斑状饱和模型,固定孔隙度(20%),改变含气饱和度。由于单元体尺度固定,所以当含气饱和度增大时,含气斑块的尺度也相应增大。采用SLS模型定量表征该组斑状饱和模型,图6显示了不同含气饱和度条件下(不同颜色)的地震波衰减和速度频散特征。对比可知,含气饱和度为20%时(图6中绿色曲线),地震波衰减的峰值最大,相应的速度频散效应也最强;均匀含水(图6中蓝色曲线)和均匀含气(图6中黄色曲线)情况下,几乎不发生衰减和速度频散。
分别对6种含气饱和度条件下的斑状饱和介质进行地震波传播模拟实验,子波函数为主频50Hz的Ricker子波,时间、空间采样间隔分别为0.05ms和1m,记录距震源200m处的质点震动速度(如图7所示)。由图7可见,当介质均匀含气或含水时,孔隙介质中的流体性质完全相同,地震波传播时无法产生较大的孔隙压力梯度,因而流体流动及引起的地震波衰减较弱,地震记录的振幅和相位几乎没有发生变化(图7中含气饱和度为0和1时)。当介质中同时充填气、水两种流体时,由于气、水的可压缩性相差较大,地震波传播过程中在气、水界面会产生较大的压力梯度,从而导致较强的流体流动和地震波衰减,地震记录的波形也会发生相应的变化。分析图6可知,含气饱和度为20%时的地震波衰减和速度频散最明显,从而导致该条件下地震记录的振幅和相位变化也最剧烈(图7);含气饱和度为40%时,地震记录也发生了较明显的变化,其它条件下地震波波形变化较小。
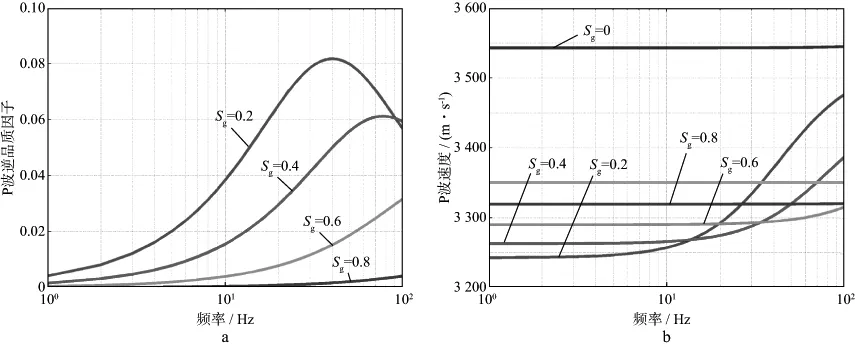
图6 孔隙度为20%时不同含气饱和度条件下地震波衰减(a)和速度频散(b)特征
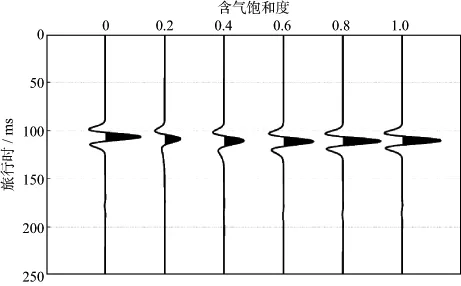
图7 不同含气饱和度条件下直达波波形对比(孔隙度为20%)
3.2 孔隙度的影响
孔隙度变化可以显著改变孔隙介质储层岩石的弹性模量和渗透率,并且影响孔隙介质的本征衰减特征。为了研究孔隙度变化对地震波传播的影响,改变孔隙度大小,不同孔隙度对应的岩石物性参数如表2所示(根据实验室测量结果[34]计算所得),储层中充填气、水两种流体,固定含气饱和度(10%),建立不同的斑状饱和储层模型。图8显示了相同含气饱和度(10%)、不同孔隙度条件下的地震波衰减和速度频散特征。由图8可见,低孔隙度条件下速度频散效应与地震波衰减显著减小,孔隙度为5%时(图8中蓝色曲线)的衰减峰值最小。孔隙度的增大,显著增强了介质对地震波的耗散能力,地震波衰减和速度频散效应也随着孔隙度的增大逐渐增强。
分别对6种孔隙度条件下的斑状饱和介质进行数值模拟实验,子波函数为主频50Hz的Ricker子波,延迟时为20ms,时间采样间隔为0.05ms,空间采样间隔为1m。图9显示了不同孔隙度条件下质点震动速度的波形记录,每道中的两个震相分别对应传播距离为0和200m时的直达波。对比分析可知,孔隙度为30%对应的地震波振幅衰减量明显高于低孔隙度条件下的地震记录,且相位也发生了明显的变化,而低孔隙度条件下的地震波能量和相位变化均较小。孔隙度增大使得干岩石的体积模量和剪切模量显著降低,岩石骨架的可压缩性增强,相同的地震波传播经过高孔隙度岩石时可以产生较大的孔隙压力梯度,引起较强的流体流动和地震波衰减,从而导致地震记录的波形发生较大的变化。此外,高孔隙度条件下地震波传播速度较低,传播200m后到达的波形有较大的延迟量。
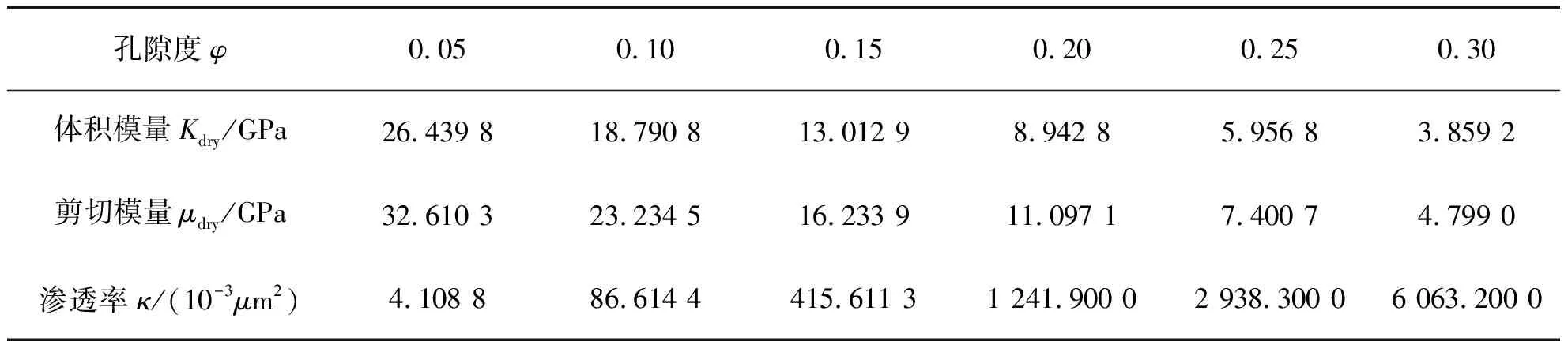
表2 不同孔隙度条件下干岩石的物性参数
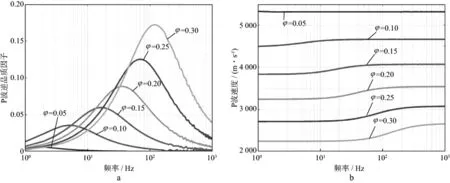
图8 含气饱和度为10%时不同孔隙度条件下地震波衰减(a)和速度频散(b)特征
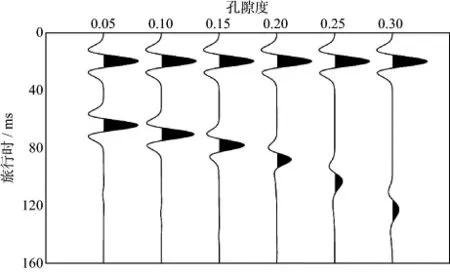
图9 不同孔隙度、相同含气饱和度(10%)条件下质点振动速度对比(每道中的两个震相分别对应传播距离为0和200m时的直达波)
4 结束语
本文将斑状饱和介质的储层参数简化为高频极限模量、低频极限模量和特征频率3个参数,采用SLS模型定量表征了介观尺度非均质储层单元的衰减和速度频散特征,同时,利用地震波传播数值模拟技术,分析了斑状饱和对地震波传播的影响。数值模拟研究结果表明:
1) SLS模型可有效地定量表征斑状饱和介质中地震波衰减和速度频散特征。
2) 利用较简单的SLS粘弹模型,可以方便快速地模拟斑状饱和介质中的地震波传播。
3) 斑状饱和介质中的强衰减和频散特征显著影响地震波记录的振幅和相位,根据SLS模型模拟的地震波记录可以比较准确地提取出斑状饱和介质中的地震波衰减和频散特征。
4) 在含气饱和度20%附近和高孔隙度的斑状饱和介质中,地震波的振幅衰减和相位变化比较大;含气饱和度和孔隙度渐变时,地震波的振幅和相位呈现相应的渐变趋势。这些波场变化特征可以为储层参数的预测研究提供分析依据。
参 考 文 献
[1] Masson Y J,Pride S R.Seismic attenuation due to patchy saturation[J].Journal of Geophysical Research,2011,116:B03206
[2] Cadoret T,Mavko G,Zinszner B.Fluid distribution effect on sonic attenuation in partially saturated limestones[J].Geophysics,1998,63(1):154-160
[3] Quintal B,Frehner M,Madonna C,et al.Integrated numerical and laboratory rock physics applied to seismic characterization of reservoir rocks[J].The Leading Edge,2011,30(12):1360-1367
[4] White J E.Computed seismic speeds and attenuation in rocks with partial gas saturation[J].Geophysics,1975,40(2):224-232
[5] Pride S R,Berryman J G,Harris J M.Seismic attenuation due to wave-induced flow[J].Journal of Geophysical Research,2004,109:B01201
[6] Toms J,Müller T M,Ciz R,et al.Comparative review of theoretical models for elastic wave attenuation and dispersion in partially saturated rocks[J].Soil Dynamics and Earthquake Engineering,2006,26(6-7):548-565
[7] Müller T M,Gurevich B,Lebedev M.Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks:a review[J].Geophysics,2010,75(5):A147-A164
[8] Johnson D L.Theory of frequency dependent acoustics in patchy-saturated porous media[J].The Journal of the Acoustical Society of America,2001,110(2):682
[9] Tisato N,Quintal B.Measurements of seismic attenuation and transient fluid pressure in partially saturated Berea sandstone:evidence of fluid flow on the mesoscopic scale[J].Geophysical Journal International,2013,195:342-351
[10] Carcione J M,Picotti S.P-wave seismic attenuation by slow-wave diffusion:effects of inhomogeneous rock properties[J].Geophysics,2006,71(3):O1-O8
[11] Ciz R,Gurevich B,Markov M.Seismic attenuation due to wave-induced fluid flow in a porous rock with spherical heterogeneities[J].Geophysical Journal International,2006,165(3):957-968
[12] Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solid I:low frequency range[J].The Journal of the Acoustical Society of America,1956,28(2):168-178
[13] Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solid II:higher frequency range[J].The Journal of the Acoustical Society of America,1956,28(2):179-191
[14] Biot M A.Mechanics of deformation and acoustic propagation in porous media[J].Journal of Applied Physics,1962,33(4):1482-1498
[15] Dutta N C,Odé H.Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (white model)—part Ⅰ:Biot theory[J].Geophysics,1979,44(11):1777-1788
[16] Dutta N C,Odé H.Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (white model)—part Ⅱ:results[J].Geophysics,1979,44(11):1789-1805
[17] Carcione J M,Helle H B,Pham N H.White’s model for wave propagation in partially saturated rocks:comparison with poroelastic numerical experiments[J].Geophysics,2003,68(4):1389-1398
[18] Rubino J G,Santos J E,Picotti S,et al.Simulation of upscaling effects due to wave-induced fluid flow in Biot media using the finite-element method[J].Journal of Applied Geophysics,2007,62(3):193-203
[19] Masson Y J,Pride S R.Poroelastic finite difference modeling of seismic attenuation and dispersion due to mesoscopic-scale heterogeneity[J].Journal of Geophysical Research,2007,112:B03204
[20] Wenzlau F,Müller T M.Finite-difference modeling of wave propagation and diffusion in poroelastic media[J].Geophysics,2009,74(4):T55-T66
[21] Rubino J G,Ravazzoli C L,Santos J E.Equivalent viscoelastic solids for heterogeneous fluid-saturated porous rocks[J].Geophysics,2009,74(1):N1-N13
[22] 王东,张海澜,王秀明.部分饱和孔隙岩石中声波传播数值研究[J].地球物理学报,2006,49(2):524-532
Wang D,Zhang H L,Wang X M.A numerical study
of acoustic wave propagation in partially saturated poroelastic rock[J].Chinese Journal of Geophysics,2006,49(2):524-532
[23] Chapman M,Liu E,Li X.The influence of fluid-sensitive dispersion and attenuation on AVO analysis[J].Geophysical Journal International,2006,167(1):89-105
[24] Rubino J G,Ravazzoli C L,Santos J E.Equivalent viscoelastic solids for heterogeneous fluid-saturated porous rocks[J].Geophysics,2009,74(1):N1-N13
[25] Picotti S,Carcione J M,Rubino J,et al.A viscoelastic representation of wave attenuation in porous media[J].Computers & Geosciences,2010,36(1):44-53
[26] Mavko G,Mukerji T,Dvorkin J.The rock physics handbook:tools for seismic analysis of porous media[M].2nd ed.Cambridge:Cambridge University Press,2009:121-127
[27] Carcione J M.Wave fields in real media:wave propagation in anisotropic,anelastic porous & electromagnetic media (Handbook of geophysical exploration,seismic exploration)[M].Amsterdam,Netherlands:Elsevier,2007:74-75
[28] Sidler R,Rubino J G,Holliger K.Quantitative comparison between simulations of seismic wave propagation in heterogeneous poro-elastic media and equivalent visco-elastic solids for marine-type environments[J].Geophysical Journal International,2013,193(1):463-474
[29] Batzle M L,Han D,Hofmann R.Fluid mobility and frequency-dependent seismic velocity—direct measurements[J].Geophysics,2006,71(1):N1-N9
[30] Gassmann F.Elastic waves through a packing of spheres[J].Geophysics,1951,16(4):673-685
[31] Hill R.Elastic properties of reinforced solids:some theoretical principles[J].Journal of the Mechanics and Physics of Solids,1963,11(5):357-372
[32] Gomez C T,Dvorkin J,Vanorio T.Laboratory measurements of porosity,permeability,resistivity,and velocity on Fontainebleau sandstones[J].Geophysics,2010,75(6):E191-E204
[33] Dutta N C,Seriff A J.White’s model of attenuation in rocks with partial gas saturation[J].Geophysics,1979,44(11):1806-1812
[34] 俞寿朋.宽带Ricker子波[J].石油地球物理勘探,1996,31(5):605-615
Yu S P.Wide-band Ricker wavelet[J].Oil Geophysical Prospecting,1996,31(5):605-615
