可变干岩石骨架等效模型研究

杨凤英，印兴耀,刘 博

(中国石油大学(华东)地球科学与技术学院，山东青岛266580)

基于岩石物理理论，结合地质、地震资料构建岩石物理模型，用测井资料作为约束可以进行储层参数预测[1-3]。Gassmann[4]给出了低频条件下饱和岩石的等效模量与岩石基质模量、干岩石骨架模量、流体模量以及孔隙度之间的关系。岩石基质模量可以用等效介质理论求解[5]。干岩石骨架弹性模量的计算方法常见的有以下几类：①实验室岩石样品直接测量干岩石骨架模量，虽然精度高但是成本也相对昂贵，不具有普遍适用性[6]。②经验公式法，如：Krief等[7]基于Raymer等[8]得到的实验数据给出了干岩石骨架模量随孔隙度变化的关系；Nur[9]提出了临界孔隙度概念，认为干岩石骨架模量随孔隙度呈线性关系；Mavko等[10]指出Nur的临界孔隙度公式与Krief等的公式基本一致。③理论计算法，如：Eshelby[11]和Walsh[12]认为岩石骨架模型不仅与孔隙度有关还与包含物纵横比有关；Kuster和Toksoz[13]根据长波一阶散射理论得到了含多种包含物形状的等效模量，即Kuster-Toksoz(K-T)理论，但该理论只适用于孔隙度与孔隙纵横比之比远小于1的情形；Pride等[14]给出了含有固结系数的岩石等效模量；Lee[15]对Pride等人公式中的剪切模量做了修改；张佳佳等[16]研究了几种岩石骨架模型的适用性，并发现Pride模型比Krief模型和Nur模型适用范围更广，且Krief模型和Nur模型对低压的低孔岩石不适用；微分等效介质(DEM)理论[17-19]通过往固体矿物相中逐渐加入包含物相来模拟双相混合物得到了耦合的微分方程组，由于方程耦合很难直接对方程积分得到精确的解析解，通常只能得到近似的数值解；Keys和Xu[20]结合K-T理论和DEM理论，在干岩石泊松比不随孔隙度变化的假设下得到了干岩石骨架弹性模量的Keys-Xu近似公式，但用他们给出的干岩石弹性模量近似式计算得到的干岩石泊松比却并不是常数。

在前人研究的基础上，我们将含有可变参数的干岩石骨架等效模量代入耦合的DEM微分方程，使得耦合的微分方程解耦为常微分方程，经一系列数学运算得到一种新的可变干岩石骨架等效模型；进一步分析可变参数的干岩石骨架等效模量的影响因素，并用实验室测量数据对可变干岩石骨架等效模型及其它干岩石等效模型进行对比测试。

1 方法原理

1.1 可变干岩石骨架模型

微分等效介质(DEM)理论可以用来计算干岩石或饱和岩石的等效弹性模量：

式中：Ki,μi为包含物相的体积模量和剪切模量；K*,μ*为加入包含物相后的体积模量和剪切模量；y为包含物含量；P,Q是给定的几何因数(Mavko等[10])；上标(*i)指的是此几何因数是针对具有等效模量K*,μ*的背景介质中的包含物材料i。

对于干岩石骨架，包含物的模量Ki=μi=0，则DEM方程变为

DEM模型之所以是耦合的是因为几何因数P,Q中含有要求解的模量信息。我们引入含有可变参数m,n的干岩石骨架等效模量：

(5)

(6)

式中：Km,μm为基质矿物体积模量和剪切模量；Kd,μd为干岩石骨架体积模量和剪切模量；m≥0,n≥0为可变参数。

将含有可变参数的干岩石骨架等效模量代替要求的模量代入文献[10]给出的P,Q表达式，就得到含有可变参数的P(m,n),Q(m,n)。这样耦合的DEM微分方程变成了常微分方程，可以对其进行求解。通过数学运算(见附录A)可以得到含有可变参数的干岩石等效弹性模量表达式，即本文导出的可变干岩石骨架等效模型(Variable Dry Rock Frame Equivalent Model,VDEM)：

其中：P(0),Q(0)与可变参数无关；P(1),Q(1)与可变参数有关，且当m=n时，P(1)=Q(1)=0，此时得到的干岩石等效弹性模量与Keys-Xu近似式的结果一致；φ为孔隙度。

1.2 可变参数对干岩石等效弹性模量的影响

以石英作为基质，模量取Km=37GPa,μm=44GPa，孔隙纵横比α=0.1，给定孔隙度范围，分析可变参数m,n对干岩石等效弹性模量的影响。首先分析m对干岩石等效模量的影响：令n=0，m从1变化到5，分析干岩石等效体积模量和剪切模量随孔隙度变化，如图1所示。再令m=0，让n从1到7变化，分析不同n时干岩石等效模量随孔隙度的变化，如图2所示。

由图1和图2可知，干岩石体积模量Kd和剪切模量μd都随孔隙度增加而减小；固定n时，在同一孔隙度条件下干岩石体积模量随m的增加而增大，剪切模量随m的增加而减小，且m对Kd影响比对μd影响更明显；固定m时，在同一孔隙度值下，干岩石体积模量随n增大而减小，剪切模量随n的增加而增大。

1.3 孔隙纵横比对干岩石等效模量的影响

同样以石英作为基质矿物，可变参数为m=4,n=1，孔隙度变化范围为0～40%，取不同孔隙纵横比α=[0.01,0.1,0.5,0.9]，分析干岩石骨架等效模量随孔隙纵横比的变化。由图3可知，在同一孔隙度条件下，干岩石体积模量和剪切模量都随孔隙纵横比的增加而增大。

图1 干岩石等效模量在不同参数m下随孔隙度的变化

图2 干岩石等效模量在不同参数n下随孔隙度的变化

图3 干岩石等效模量随孔隙纵横比α的变化

2 实验室数据对比分析

用Han等[21]在40MPa压力下测得的砂岩数据对本文导出的可变干岩石骨架等效模型进行测试。首先用Han等给出的方法计算岩石基质模量，然后用测量得到的饱和岩石的纵波速度、横波速度以及密度计算得到饱和岩石模量，最后根据Gassmann方程计算干岩石骨架模量。将计算结果与Nur公式，Lee公式以及本文导出的可变干岩石骨架等效模型得到的干岩石骨架弹性模量进行对比，所得结果如图4和图5所示。表1给出了所需公式及参数。

图4 基于文献[21]在40MPa压力下实测砂岩数据的干岩石骨架体积模量计算结果对比

图5 基于文献[21]在40MPa压力下实测砂岩数据的干岩石骨架剪切模量计算结果对比

参数Kdμd其它参数Nur公式Kd=Km1-φφc()μd=μm1-φφc()临界孔隙度φc=0.4Lee公式Kd=Km1-φ1+cφμd=μm1-φ1+rcφ,r=1+2c1+c固结系数c=4VDEMKd=Km(1-φ)P(0)+P(1)eφP(1)μd=μm(1-φ)Q(0)+Q(1)eφQ(1)m=4,n=1α=0.2

从图4中可以看到，含有固结系数的Lee公式得到的干岩石骨架体积模量相对误差主要为负值，说明得到的干岩石体积模量偏小；从干岩石骨架体积模量相对误差上来看，可变干岩石骨架等效模型(VDEM)和Nur公式得到的结果优于Lee公式的结果，但VDEM所得干岩石骨架体积模量的相对误差比Nur公式得到的相对误差更为集中且分布在0附近，说明VDEM得到的干岩石等效体积模量和Han测得的结果更为接近。

由图5可知，Nur公式得到的干岩石骨架剪切模量相对误差大部分为正，说明其计算结果整体偏大；VDEM得到的干岩石骨架剪切模量与Lee公式得到的结果相比，VDEM所得结果的相对误差小且集中分布在0附近，说明VDEM得到的干岩石等效剪切模量精度更高。

3 结束语

通过引入含有可变参数的干岩石骨架等效模量将耦合的微分等效介质方程进行解耦，进一步化简得到可变干岩石骨架等效模型(VDEM)。可变干岩石骨架等效模型避免了求解耦合的微分方程，使问题得到简化，提高了干岩石骨架等效弹性模量的计算效率。且该模型得到的干岩石骨架弹性模量不仅与矿物基质有关，还与孔隙度以及表征孔隙形状的孔隙纵横比有关，与其他经验公式相比提高了模型的适用性。基于实验室测量数据的试算结果表明，与其他干岩石骨架弹性模量公式的计算结果相比，可变干岩石骨架等效模型提高了干岩石骨架等效弹性模量的预测精度。

附录A 可变干岩石骨架模型公式推导

(A1)

式中：

其中：a=3Km+4μm，b=3nKm+4mμm，c=3μm，d=3mμm；f，θ是包含物纵横比的函数(具体形式请参见文献[10])。

对于干岩石骨架有Ki=μi=0，DEM方程变为

用上述的P替换方程(A8)中的P(*i)(y)可得到：

(A10)

将(10)中的y从0到φ积分可以得到：

(A11)

由此可以得到含有孔隙度为φ的干岩石等效体积模量K(φ)：

(A12)

式中：P(0)与可变参数m,n无关，而P(1)与两个可变参数有关，且当m,n相等或都为0时，可以得到P(1)=0，此时干岩石等效体积模量为K(φ)=Km(1-φ)P(0)。这个结果与Keys等[20]给出的干岩石体积模量近似式一致。

同理可得几何因数Q的表达式：

(A13)

其中：

B7=5(D3D10+D4D9+D5D8)

(A30)

B8=5(D4D10+D5D9)

(A31)

B9=5D5D10(A32)D1至D10分别为

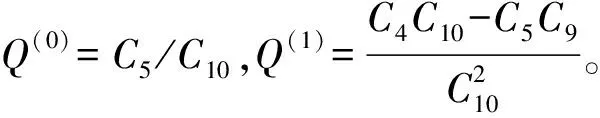
(A33)

将(A33)对y从0到φ进行积分，可以得到

(A34)

因此含有孔隙度φ的干岩石等效剪切模量为

(A35)

式中：Q(0)与可变参数m,n无关，Q(1)和两个调节参数有关，且当m,n相等或都为0时，可以得到Q(1)=0，此时的干岩石等效剪切模量为μ(φ)=μm(1-φ)Q(0)，这个结果也与Keys-Xu近似式给出的干岩石剪切模量近似结果一致。

参 考 文 献

[1] 郭栋,印兴耀,吴国忱.横波速度计算方法与应用[J].石油地球物理勘探,2007,42(5):535-538

Guo D,Yin X Y,Wu G C.Methods of S-wave velocity computation and its applications[J].Oil Geophysical Prospecting,2007,42(5):535-538

[2] 周中彪.基于岩石物理模型的测井约束横波速度计算方法研究[J].物探化探计算技术,2010,32(5):536-541

Zhou Z B.The study on S-wave velocity calculation method constrained by logging based on rock physics models[J].Computing Techniques for Geophysical and Geochemical Exploration,2010,32(5):536-541

[3] 刘欣欣,印兴耀,张峰.一种碳酸盐岩储层横波速度估算方法[J].中国石油大学学报(自然科学版),2013,37(1):42-49

Liu X X,Yin X Y,Zhang F.An approach to predict S-wave velocity of carbonate rocks[J].Journal of China University of Petroleum,2013,37(1):42-49

[4] Gassmann F.Über die elastizität poroser medien[J].Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich Vier，1951,96(1):1-23

[5] 印兴耀,刘欣欣,曹丹平.基于Biot相洽理论的致密砂岩弹性参数计算方法[J].石油物探,2013,52(5):445-451

Yin X Y,Liu X X,Cao D P.Tight sandstone elastic parameters calculation method based on Boit-Consistent theory[J].Geophysical Prospecting for Petroleum,2013,52(5):445-451

[6] Murphy W F.Acoustic measures of partial gas saturation in tight sandstones[J].Journal of Geophysical Research,1984,89(B13):11549-11559

[7] Krief N,Garat J,Stellingwerff J,et al.A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic)[J].The Log Analysis,1990,31(6):355-369

[8] Raymer L L,Hunt E R,Gardner J S.An improved sonic transit time-to-porosity transform[J].SPWLA 21stAnnual Logging Symposium,1980:1-12

[9] Nur A.Critical porosity and the seismic velocities in rocks[J].Eos,Transactions American Geophysical Union,1992,73(1):43-66

[10] Mavko G,Mukerji J,Dvorkin J.The rock physics handbook:tools for seismic analysis in porous media[M].NewYork:Cambridge University Press,2003:1-329

[11] Eshelby J D.The determination of the elastic field of an ellipsoidal inclusion,and related problems[J].Proceedings of the Royal Society of London,1957,241(1226):376-396

[12] Walsh J B.The effective of cracks on the compressibility of rock[J].Journal of Geophysical Research,1965,70(2):381-389

[13] Kuster G T,Toksoz M N.Velocity and attenuation of seismic waves in two-phase media:Part I,theoretical formulations[J].Geophysics,1974,39(5):587-606

[14] Pride S R,Berryman J G,Harris J M.Seismic attenuation due to wave-induced flow[J].Journal of Geophysical Research,2004,109:B01201

[15] Lee M W.A simple method of predicting S-wave velocity[J].Geophysics,2006,69(5):161-164

[16] 张佳佳,李宏兵,刘怀山,等.几种岩石骨架模型的适用性研究[J].地球物理学进展,2010,25(5):1697-1702

Zhang J J,Li H B,Liu H S,et al.Accuracy of dry frame models in the study of rock physics[J].Process of Geophysics,2010,25(5):1697-1702

[17] Cleary M P,Lee S M,Chen I W.Self-consistent techniques for the heterogeneous media[J].Journal of the Engineering Mechanics Division,1980,106(5):861-887

[18] Norris A.A differential scheme for the effective moduli of composites[J].Mechanics of Materials,1985,4(1):1-16

[19] Zimmerman R W.Compressibility of sandstones[M].New York:Elsevier,1991:1-173

[20] Keys R G,Xu S.An approximation for the Xu-White velocity model[J].Geophysics,2002,67(5):1406-1414

[21] Han D H,Nur A,Morgan D.Effects of porosity and clay content on wave velocities in sandstones[J].Geophysics,1986,51(11):2093-2107