一种加权的系统聚类方法及应用
2014-03-25原忠虎
原忠虎, 李 佳, 张 博
(沈阳大学 信息工程学院, 辽宁 沈阳 110044)
自从改革开放以来,我国的物流业已历经了几十年的发展.在国家政策的大力支持下,我国物流业已成为国民经济发展的重要支撑.随着物流成本上升、竞争加剧等问题日趋严重,客户关系管理已成为物流企业的关注点之一[1].
客户聚类分析是物流企业客户关系管理领域中的一个研究重点.客户聚类分析可以对客户进行分类,从而达到为不同特征的客户提供个性化服务的目的.在客户聚类分析研究中,系统聚类是一种应用较多的聚类方法.系统聚类是利用样本间距离最近的原则进行聚类的方法,整个聚类过程可用一张谱系图形象地表示[2].目前有研究使用系统聚类方法解决CRM中的聚类分析问题[3].
目前研究使用系统聚类进行客户聚类分析的过程中,对各个特征的重要性不加区别,即聚类对象的相似属性越多,对象间越相似.但是,目前物流企业运营过程中,由于不同企业的经营理念不同,对客户不同特征的重视程度不同,因此,聚类过程中,企业重视的客户特征应具有较高的权重,从而使该特征在聚类过程中起到较大的决定作用.
基于以上分析,本文提出加权的系统聚类方法,通过对不同的特征赋予不同的权值,使企业重视的特征在聚类过程中有更高的影响,从而达到根据企业自身的运营特征进行客户聚类分析的目的.
实验表明,根据线性回归可以正确地发现物流企业重视的客户特征,并且聚类的结果基本符合基于企业所重视的客户特征对客户进行划分的结果.
1 基于线性回归的特征权重的计算
本文利用线性回归方法,从大量公司运营的数据中挖掘客户的每种特征对公司运营的重要程度.
在统计学中,线性回归(Linear Regression)是指利用线性回归方程的最小平方函数对一个或多个自变量和因变量之间的关系进行建模.这种函数是一个或多个被称为回归系数的模型参数的线性组合.在线性回归中,数据使用线性预测函数来建模,并且未知的模型参数也是通过数据来估计的.这些模型被叫作线性模型[4].线性回归模型经常用最小二乘逼近来拟合. 最小二乘法是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配.利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小[5].其经验拟合方程的相关系数可用以下公式计算[4]:
(1)
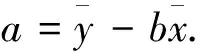
(2)
假设某物流公司2001—2013年的年利润数据如表1所示,用线性回归方法计算这家公司对客户年利润数据特征的重视程度.

表1 某物流公司年利润数据表Table 1 The annual profit data table of a logistics company

2 加权的系统聚类方法
2.1 加权的系统聚类方法的原理
系统聚类属于层次聚类分析方法, 是一种逐次合并类的方法, 最后得到一个聚类分析谱系图[3]. 其方法是: 先将n个样本各自看成一类,计算两两样本之间的距离,得到一个距离矩阵;然后将距离最近的两类合并为新类,并计算新类与其他类之间的距离,再将距离最近的两类合并;逐次这样进行下去,直到把所有的样本合并为一类为止[6].
以上是聚类的具体过程,在这个过程中,计算距离时每个特征的权重相同,但是在物流公司对其客户聚类的过程中,由于公司对客户各类特征的重视程度不同,所以对不同的特征要加以不同的权重.例如,重视程度高的特征加以更大的权重,从而使该特征在聚类过程中起到较大的作用.
2.2 预处理方法和原理
对样本数据进行预处理, 以削弱异常数据对整个聚类过程的影响.预处理过程可分为4个步骤.
第1步 对客户特征的指标进行选定与度量;
第2步 确定每一特征的语言变量和隶属函数;

第4步 根据最大隶属度法,取

由此得到新数据表.
每个步骤的具体过程如下.
在客户特征指标的选定与度量过程中,定义待聚类的客户样本集为S={S1,S2,S3,…,Sn}.其中,n代表样本信息表中样本的数量,Si代表第i个客户.对物流企业的重点客户进行客户群体划分.根据对物流企业的研究,可以选出毛利润、货物类型、托运货物总件数、客户名称这四个对客户价值影响较大的变量作为物流企业客户特征描述的指标,记Xi=(Xi1,Xi2,Xi3,Xi4)(i=1,2,3,…,n).其中,Xij代表第i个客户样本相对于第j个指标的值.于是得到n×4 阶矩阵X=(Xij),称为原始信息矩阵.
确定每一特征的语言变量值和隶属函数的过程如下.例如,指标中含有定性描述(货物类型、客户)指标,假设物流企业为客户托运的货物有饮料、化妆品、建材三种,则这三种货物类型可根据物流企业托运的频率相应地设为权重1、2、3;指标中还含有数值类的指标,如物流企业5次托运货物的毛利润分别为100元、160元、200元、230元、300元,则其对应的模糊语言变量如下:1代表毛利润100元,2代表毛利润200元,3代表毛利润300元.
根据隶属函数,把对象的每一特征转化为函数形式.具体如下:
fori=1 tom, forj=1 ton.
对象的条件特征值转化为如下形式:
(3)

经过以上步骤的客户信息预处理后,就把所有的特征指标都转化为定量指标,为下一步的加权聚类提供了有力保障.
2.3 加权聚类
由于预处理过程把所有的指标都转换为定量指标,另外, 各指标的量纲不全相同, 因此,接下来需要把各特征指标数据标准化.令

把各指标数据标准化后得到矩阵S,如下:
(5)
得到标准数据矩阵S后,按照传统的系统聚类方法,矩阵S中的各项特征无区别,也就是各特征的权重相同.但是,企业在实际的运营中,会根据本公司的经营理念,对客户特征有不同的重视程度,所以要为企业重视的特征加权重.所加权重值就是用线性回归的方法计算出的权重值b,把计算出的权重值加到相应的客户特征上,例如,计算第一个特征的权重值,矩阵如下:
(6)
对矩阵不加权的S样本和加权的S′样本进行样本间的相似度量,也就是距离的计算.开始时,n个样本Si看成n个类Gi,计算其两两间的距离.确定方法有很多种,如绝对距离、欧式距离、离差平方和距离等.这里采用较简单的绝对距离.公式如下:
(7)
经过样本间距离计算后构成一个对称距离矩阵,如下:
(8)
式中,Dab为Ga与Gb两类之间的距离.
选择矩阵D中的非对角线上元素的最小值,设这个值为Dab,将Ga与Gb合并成新类Gv.任两类Gv与Gk之间的距离Dkv为Dkv=min{Dka,Dkb},即用两类中样本之间的最短距离者作为两类之间的距离.在D中消去Ga与Gb所对应的行和列, 并且加入由新类Gv与剩下未聚合的类间的距离所组成的一行和一列, 得到一个新的距离矩阵D1,它是n-1阶矩阵.
从D1出发, 重复计算各样本间的距离, 直到n个样本类聚合为预定的类个数时为止.在合并过程中记下合并类的编号,最终得到的合并样本编号即为一类.
3 加权系统聚类方法实例分析
对实例分析的过程大体分为四步,首先对提供的客户数据进行预处理,其次对预处理的数据进行不加权聚类,然后对预处理的数据进行加权聚类,最后对不加权的聚类结果和加权的聚类结果进行对比分析.
3.1 数据预处理
表2是某物流企业部分客户的信息资料表,表中记载了物流公司为客户托运货物的详细情况.

表2 客户信息资料表Table 2 Customer information date table


表3 模糊转换后的客户资料信息表Table 3 Customer information after blur conversion
由表3,根据最大隶属度法,取

由此得到表4.

表4 模糊量化的客户资料信息表Table 4 Customer information after blur quantify
在聚类过程中,不考虑时间特征,将表4中月份列去掉后标准化得到矩阵S:
3.2 不加权的聚类过程
由于不需要加权值,所以直接由矩阵S计算得到距离矩阵D:
找出D中非对角最小数值是0.13,由矩阵中可以找到数值0.13对应的是S2和S9之间的距离,记为D2,9=0.13,所以将S2,S9合并为一类,记为G12={S2,S9},再计算G12与其他类之间的距离得到D1,直到n个样本类都聚合为预定的类个数为止.
经过逐步计算后,得到客户聚类分析图,如图1所示.

图1 不加权的聚类分析图Fig.1 Unweighted cluster analysis diagram
3.3 加权的聚类过程
特征权重是利用线性回归的方法计算得出的,各个特征权重的计算过程、结果如下.
托运货物总件数的权重:
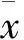
货物类型的权重:
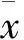
客户名称的权重:

毛利润的权重:

得到各个特征的权重后,把矩阵S的各个特征加权重后得到矩阵S′:
由矩阵S′计算得到距离矩阵D′:
经过逐步计算后,客户的各类特征加权重的聚类分析图如图2所示.

图2 加权重的聚类分析图Fig.2 Weighted cluster analysis diagram
3.4 实例分析结论
经过两个步骤的计算后,根据图1和图2的聚类分析结果可以看到,图1中分成两类客户,第1类包括样本S1~S10,第2类只包括一个样本S11;图2中分成两类客户, 第1类包括样本S1~S3,S5~S10,第2类包括样本S4和S11.由以上结果可以看到图1和图2聚类结果的明显区别是样本S4在客户各类特征加权重后和样本S11分为一类,由表2的客户信息表可以计算出,为样本S4托运货物每件的利润是75元,样本S11每件的利润是60元,而其他的样本S1,S3,S5,S6,S7,S8,S9,S10每件的平均利润是10~40元.以上数据表明,在物流公司重视每件货物的托运毛利润的情况下,如果没有对客户特征加权重,则可能把利润较高和利润相对较低的分为一类,而对特征加权可以降低该情况发生的概率.
4 结 语
在物流企业客户关系管理中,客户聚类分析中的系统聚类是该领域中的一个研究重点,但是物流企业目前一般采用传统的系统聚类方法.传统的聚类方法的一个重要特点是在聚类过程中对特征都采取相同的重视程度,但是在企业的实际运营过程中,对客户的特征有不同的重视程度,所以采用传统的聚类方法就容易把一般客户和重要客户混淆, 使公司不能有效地进行客户关系管理.本文提出加权的系统聚类方法,利用线性回归得到物流企业对客户各个特征的重视程度,并把重视程度作为权值进行客户聚类.实验表明,加权的系统聚类方法可以降低一般客户和重要客户混淆的概率,发现隐藏在一般客户中的重要客户,从而使物流企业对本公司的重要客户提供优质服务,为维持良好的客户关系打下坚实的基础,从而使企业和客户达到双赢的目的.
参考文献:
[1]王春辉. 第三方物流企业客户关系管理研究[D]. 大连: 大连理工大学, 2011:1-51.
(Wang Chunhui. Research on Customer Relationship Management in Third-Party Logistics Enterprise[D]. Dalian: Dalian University of Technology, 2011:1-51.)
[2]柳卓. 系统聚类方法在洪水预报中的应用研究[D]. 杭州:浙江大学, 2007:1-66.
(Liu Zhuo. The Application of Hierarchical Clustering Method in the Study of Flood Forecast[D]. Hangzhou: Zhejiang University, 2007:1-66.)
[3]唐志航,杨保安. 系统聚类在客户关系管理中的研究与应用[J]. 计算机工程与应用, 2007,43(13):220-223.
(Tang Zhihang, Yang Bao’an. Investigation and Application of Hierarchical Clustering in Customer Relationship Management[J]. Computer Engineering and Applications, 2007,43(13):220-223.)
[4]宋欣,王翠荣. 基于线性回归的无线传感器网络分布式数据采集优化策略[J]. 计算机学报, 2012,35(3):568-580.
(Song Xin, Wang Cuirong. Linear Regression Based Distributed Data Gathering Optimization Strategy for Wireless Sensor Networks[J].Chinese Journal of Computers, 2012,35(3):568-580.)
[5]吴琼,原忠虎,王晓宁. 基于偏最小二乘回归分析综述[J]. 沈阳大学学报, 2007,19(2):33-35.
(Wu Qiong, Yuan Zhonghu, Wang Xiaoning. Summary of Partial Least Squares Regression[J]. Journal of Shenyang University, 2007,19(2):33-35.)
[6]李斌,郭剑毅. 一种带约束的最小离差平方和系统聚类法及应用[J]. 计算机应用, 2005,25(1):45-48.
(Li Bin, Guo Jianyi. Method and Application of Restricted Minimum Variance Hierarchical Cluster[J]. Computer Applications, 2005,25(1):45-48.)
