齿轮滚刀优化及其仿真
2014-03-25孟清申金丹廉哲满
孟清, 申金丹, 廉哲满
( 1.延边大学工学院 机械工程系, 吉林 延吉 133002; 2.延边大学 科技处, 吉林 延吉 133002 )
齿轮传动是机械传动中最重要的传动之一.齿轮的使用寿命往往决定着产品的使用寿命.工作中齿根处应力过大而造成的齿轮轮齿折断是齿轮的主要破坏形式之一[1].研究[2]表明,齿根处的最大应力与齿根过渡曲线的形状有关,而齿根过渡曲线的形状又与齿轮加工刀具顶刃圆角半径有关.在齿轮生产中,对齿轮加工刀具顶刃圆角半径通常不做严格规定,一般取0.25 m~0.3 m[3](m为被加工齿轮的模数).为优化齿轮设计,王亮等[4]通过ANSYS软件对齿轮进行了有限元分析,并提出了对齿轮结构的改进方案;芮井中等[2]提出了一种有效地描述齿根过渡曲线形状的参数化方法,对以获得齿根最小弯曲应力为目标的齿根过渡曲线进行了优化.由于滚刀具有高精度、高效率等优点[5],目前成为最广泛使用的一种齿轮加工刀具.为了改善滚刀齿根受力情况,本文以普通滚刀为例对其顶刃圆角进行优化,以延长齿轮使用寿命.
1 齿轮加工仿真系统
1.1 齿轮加工仿真系统的开发
以Visual Basic 6.0为开发工具对AutoCAD 2004进行二次开发,以此实现齿轮加工仿真.仿真的思想是将实际加工过程进行离散化,离散后的每个单元采用布尔运算完成材料的去除工作,然后将所有单元整合为一体,形成连续的切削加工过程.滚齿采用范成法加工原理,并且将滚刀切削齿坯的过程按齿条切削齿坯的过程处理[6].由于滚刀结构复杂,其仿真效率较低,所以采用结构简单的齿条代替滚刀,以提高仿真效率和精度.仿真加工时,齿条与齿坯做范成运动,即齿条水平移动速度等于齿坯节圆旋转线速度.图1和图2分别为齿轮加工仿真系统界面和齿轮加工仿真过程.
图1 齿轮滚刀加工仿真系统界面
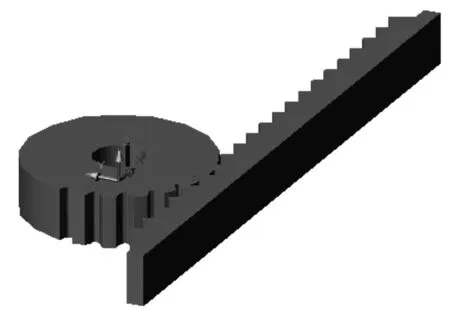
图2 齿轮加工仿真过程
1.2 齿齿轮加工仿真系统的校验
为了验证仿真系统的加工效果,将被加工齿轮齿廓与标准齿轮齿廓进行对比分析.轮模数是决定齿轮齿廓和齿轮各个尺寸的重要参数,本文选用3组齿轮进行对比,其模数分别为2、5和8,齿数均为20,齿轮齿廓对比图如图3所示.图中曲率较大的齿根过渡曲线是用Pro/E创建的标准齿轮齿廓,其曲率半径按国家规定取为0.38 m[7],曲率较小的是仿真系统加工出的齿轮齿廓.从图3可以看出,理论齿廓与标准齿廓几乎完全重合,但各组齿轮齿廓的齿根过渡曲线不重合,这表明本文仿真系统的仿真效果良好.齿根过渡曲线不重合的原因在于标准齿轮的齿根过渡曲线为圆弧,而利用范成法加工出来的齿轮齿根过渡曲线为延伸渐开线的等距曲线[7].
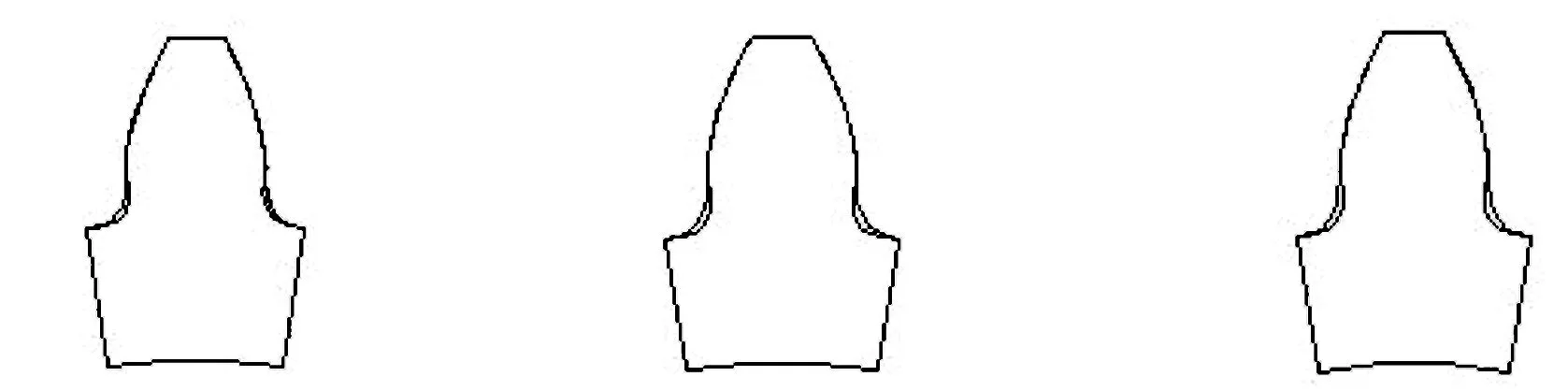
a)齿轮模数2 b)齿轮模数5 c)齿轮模数8图3 齿廓对比图
2 滚刀顶刃圆角半径、齿根过渡曲线与齿根受力情况之间的关系
2.1 滚刀顶刃圆角半径与齿根过渡曲线之间的关系
延伸渐开线的等距曲线的变化比较复杂,如果通过数学表达式进行比较,其计算量会很大,所以本文采用比较直观的方法,即通过将齿廓重叠来比较各齿轮的齿根过渡曲线.当其他参数相同,刀具顶刃圆角分别为0.5、1.0、1.5 mm时,仿真出来的齿根过渡曲线分别为图4所示的1、2、3号曲线,其中右图是左图齿根过渡曲线的局部放大图.从图中可以看出,齿轮中1、2、3号齿根过渡曲线的曲率越来越小,也就是说滚刀圆角半径越大,加工出的齿根过渡曲线曲率越小.

图4 齿根过渡曲线对比
2.2 齿根过渡曲线与齿根受力情况之间的关系
用ANSYS中的Workbench模块分别对3个齿轮进行受力分析.为了便于观察,Pro/E建模后分别从3个齿轮中截取1个齿进行分析.齿轮材料为45#钢,其弹性模量E=2.05×1011MPa,泊松比μ=0.3,密度ρ=7 800 g/mm3,其约束条件加在左右两个截面上,力添加到齿顶处一块很小的面上,力的大小按下列条件计算:齿轮转速n=1 470 r/min,传动功率p=18 kW,计算得到切向力Ft=2 338.78 N,法向力Fr=851.25 N,其分别加在x和y方向.应力分布图如图5所示,其中图a、b、c的齿根过渡曲线分别对应图4中的1、2、3号曲线.从图中可以看出,应力主要集中在齿根部位,呈深色部分.另外,图中显示的最大应力分别为σ1=91.571 MPa,σ2=81.72 MPa,σ3=77.556 MPa,这说明随着齿根曲率的减小,齿根部位最大应力在减小.

图5 齿轮单个齿应力分布对比图
综上所述,齿轮加工刀具的顶刃圆角越大,齿根过度曲线的曲率越小;齿根过渡曲线的曲率越小,齿根部位的最大应力越小.也就是说,齿轮加工刀具的顶刃圆角半径越大,齿根部位的最大应力就越小.
3 滚刀顶刃圆角优化及其效果验证
3.1 滚刀顶刃圆角优化
虽然刀具顶刃圆角越大越好,但要加工出正确的齿轮还必须满足两个条件:①齿轮的有效渐开线要足够长,以保证齿轮在啮合时不发生干涉;②刀具的齿顶高应符合标准,以保证被加工齿轮的齿根圆尺寸符合标准.要加工出足够长的渐开线长度就得保证刀具与齿轮啮合最低点的啮合半径小于被加工齿轮与其配对齿轮啮合最低点的啮合半径.
齿条刀具与被加工齿轮的啮合图如图6所示,图中D点是最低啮合点,CD是啮合线.设BD=x,z为齿轮齿数,k=3.141 6r/2z,α为被加工齿轮的压力角,r为被加工齿轮的分圆半径,R为刀具与齿轮啮合的最低点啮合半径,则由图6中的几何关系可求得:
(1)
被加工齿轮与其配对齿轮(这里选用配对齿轮齿数为40)啮合图如图7所示.图中r1和r2分别为齿轮1和齿轮2的节圆半径,rb1和rb2分别为齿轮1和齿轮2的基圆半径,a为两齿轮的中心距,m为齿轮模数,α为齿轮节圆压力角,αa2为齿轮2的齿顶圆压力角,z1和z2分别为齿轮1和齿轮2的齿数,rk为被加工齿轮与其配对齿轮啮合时最低点的啮合半径.
αa2=arccos(rb2/ra2)=
(2)
(3)
由于R≤rk, 解得
x≥(rcosα+ksinα)-
(4)

图6 刀具与被加工齿轮的啮合图

图7 被加工齿轮与其配对齿轮的啮合图
刀齿截面图如图8所示.图中rd为刀具顶刃圆角半径,h为刀齿的齿顶高,由几何关系可得
rd=(h-x)/(1-sinα).
(5)
由(5)式可以看出,x取值越小,rd越大.加工过程中为了保证正确的齿根圆尺寸,需要保证刀齿的齿顶高h符合标准值,所以当x取最小值时,rd能否取到最大值,还需做进一步讨论.
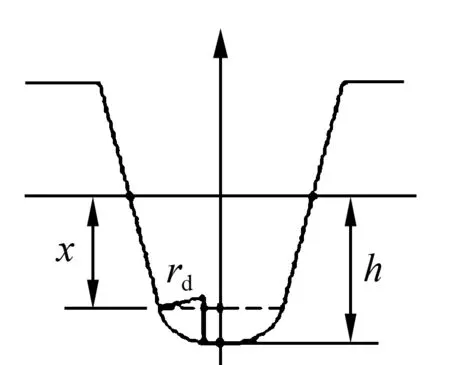
图8 刀齿截面图
刀具设计过程中可能出现3种情况(见图9):①xmin加圆弧高度比h小,切出的齿根圆偏大;②xmin加圆弧高度等于h, 即最理想情况; ③xmin加圆弧高度比h大,切出的齿根圆偏小.第1种情况首先要保证刀齿齿顶高等于h, 第3种情况首先要保证x取值不小于xmin.对图9 b进行几何求解,可解得xmin的临界值为
xmin=h(1+sinα)-kcosα.
(6)
综上所述,当xmin≤h(1+sinα)-kcosα时,滚刀顶弧可用单圆弧,rd最优解为
rd=(kcosα-hsinα)/(1-sinα).
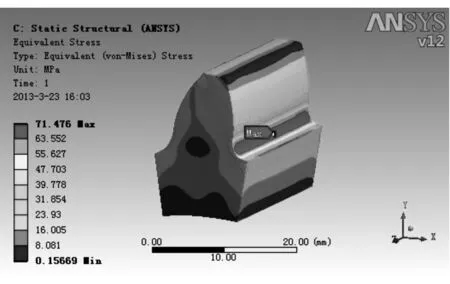
当h(1+sinα)-kcosα≤xmin a b c图9 滚刀顶刃可能出现的3种情况 通过编程将上述优化过程植入仿真系统,在系统界面输入相应的参数后,系统会自动对加工进行优化,并将此刀具加工出来的齿轮导入到ANSYS的Workbench模块中进行有限元分析.将该分析结果与前面几组未优化的分析结果进行对比,即可验证优化效果.同上,被检测齿轮模数为5,齿数为20,其配对齿轮齿数选为40,分析结果如图10所示.优化后滚刀加工出的齿轮齿根部位的最大应力σ=71.476 MPa,较之前有较大幅度地提高,说明优化效果较好. 图10 优化后的齿轮应力分布图 优化后的齿轮能否正常工作,还需要在工作状态下对啮合的齿轮进行干涉检测.检测方法是将被加工齿轮及其配对齿轮导入Pro/E中,用运动仿真模块对两个齿轮进行啮合运动仿真.与此同时,利用运动仿真模块中的干涉检查功能对啮合齿轮进行干涉检测.如果齿轮啮合时出现干涉现象,则仿真中会出现干涉条纹,如果无干涉现象则齿轮将正常运行.图11是将两个齿轮中心距缩短1 mm后的检测图,图12是两个齿轮正常啮合状态下的检测图.检测结果显示:两个齿轮在啮合过程中未出现干涉现象,说明优化过程合理. 图11 运动干涉图 图12 正常运动图 本文首先以Visual Basic 6.0为开发工具对AutoCAD 2004进行二次开发,完成了齿轮加工仿真,并验证了该仿真系统具有良好的仿真效果.在此基础上,对滚刀顶刃圆角半径、齿根过渡曲线与齿根受力情况之间的关系进行了研究,结果表明齿轮加工刀具的顶刃圆角半径越大,齿根部位的最大应力就越小.最后以滚刀顶刃圆角半径最大化为优化目标,利用齿轮加工的两个必要条件对滚刀顶刃圆角半径进行了优化计算,并对其优化结果及运动干涉进行了检测.结果表明,本文提出的优化方法效果良好,可有助于减小齿轮齿根最大弯曲应力,延长齿轮的使用寿命. 参考文献: [1] 濮梁贵,纪名刚.机械设计[M].8版.北京:高等教育出版社,2006:187. [2] 芮井中,吴学志.齿根过渡曲线优化方法研究[J].机械传动,2010,34(2):38-40. [3] 袁哲俊,刘华明,唐宜胜.齿轮刀具设计[M].北京:新时代出版社,1983:261. [4] 王亮,王展旭,杨眉.基于ANSYS的渐开线直齿圆柱齿轮有限元分析及改进方法[J].现代制造工程,2008(4):66-68. [5] 杨选文,余功炎,文卫无.滚刀设计发展趋势的分析[J].汽车工艺与材料,2007(6):39. [6] 丁彩虹,杨向萍.滚齿加工过程的计算机模拟系统设计[J].机械与电子,2003(2):51. [7] 庄中.齿顶整圆弧滚刀的应用和设计[J].汽车工艺与材料,2005(8):22-25.
3.2 优化效果验证
3.3 干涉检测


4 结束语
