量子力学中能量算符的分析与讨论
2014-03-25赵培茈朱爱东
赵培茈, 朱爱东
( 延边大学理学院 物理系, 吉林 延吉 133002 )
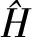
1 算符和哈密顿量物理意义的界定
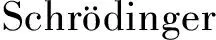
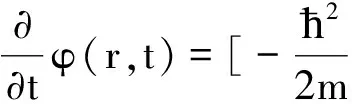
(1)
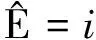
(2)
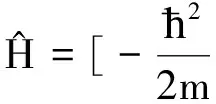
(3)
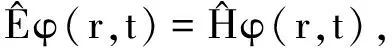
(4)
其能量本征方程为
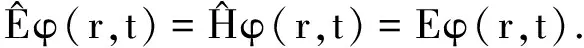
(5)
从量子力学中的算符化规则来看,在坐标表象中对于非定态问题所有的力学量需作变换:r→r,p→-iħ,而哈密顿量中组成能量的具体力学算符都符合这种变换,这样哈密顿量就能在坐标表象中具体描写.能量算符对于任何系统都只有一种不变的形式,即(2)式的形式,它不能表示成关于坐标的算符.二者通过薛定谔方程联系起来,用于求解系统的时间演化规律.但无论和形式如何,它们都对应于量子力学的同一可观测量——能量,只是对波函数的作用结果不同而已,其物理本质是相同的,在这一点上它们没有任何区别.
2 算符和哈密顿的作用分析
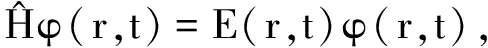
(6)

(7)
求解方程(6)可得能量本征值E(r,t), 将E(r,t)代入(7)式并求解得
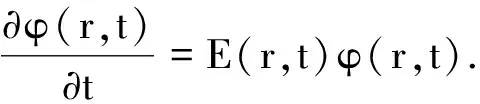
上式两端对时间积分得
(8)
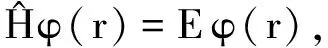
(9)
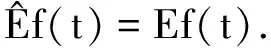
(10)
由(9)式可求得φ(r)和能量本征值E, 由(10)式可求得f(t)(在波函数已知的情况下也可求得能量本征值E),于是有:
E=∑|Cn|2En,
(11)
(12)
3 结论
参考文献:
[1] 曾谨言.量子力学教程[M].2版.北京:科学出版社,2008:15-22.
[2] 周世勋.量子力学教程[M].2版.北京:高等教育出版社,1979:72-82.
[3] 褚圣麟.原子物理学[M].北京:高等教育出版社,1979:82-89.
[4] 李春芳,王奇.量子力学中的时间和能量算符[J].上海大学学报:自然科学版,1997(11):278-280.
[5] 欧贤守.关于时间-能量测不准关系[J].安庆师范学院学报,1992(1):14-15.
[6] 郭贵春,赵丹.论能量-时间不确定关系的解释语境[J].自然辩证法通讯,2007(2):17-23.
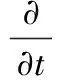
[9] 王智勇,熊彩东.量子力学中的时间[J].物理学报,2007(6):3070-3075.
[10] 吴新忠.量子论的一种进化论解释[J].武钢职工大学学报,1999(4):10-19.
