股票价格的灰色预测模型
2014-03-25金明爱程隆昌
金明爱, 程隆昌
( 天津财经大学理工学院 数学系, 天津 300222 )
在证券市场中,投资者通常利用股票收盘价的历史数据及其相关因素来预测股票收盘价未来的变化趋势,以便做出正确的投资选择.为了能更准确地把握股价的变化趋势,近年来股价理论的研究受到了广泛的关注,也取得了一些研究成果[1-3],但其中大多偏重于定性描述和分析,而缺少定量分析.另外,从投资者能够获取的数据来看,数据越新对投资者的预测影响越大,但由于新数据只占全部数据中的一少部分,因此,对过去历史数据的预处理是未来预测中的重要环节.本文将股票市场作为灰色系统,利用灰色理论和方法[4]对采用的股票收盘价数据进行生成处理,然后根据灰色系统理论中的“新信息优先原理”,建立灰色GM(1,2)模型,以期为投资者优化投资组合提供参考数据.
1 灰色预测GM(1,2)模型
自1982年中国学者邓聚龙创立灰色系统理论以来,该理论已渗透到自然科学和社会科学的许多领域,得到了广泛的应用[5].针对一些传统预测模型的预测结果精度不够理想等问题,很多学者对原始模型进行了优化和改进[6-11].其中文献[7]从GM(1,1)的灰导数生成出发,论证了将向前差商和向后差商的加权平均值作为GM(1,1)的灰导数白化值的合理性.本文基于文献[4]中求待辨识参数的方法,建立了GM(1,2)预测模型.

其中a,b是待辨识参数,其离散的白化时间响应函数为
(1)
(2)
(3)
令
(4)
则(3)式变为
(5)
取k=2,3,…,k, 并代入(5)式可依次得:
⋮
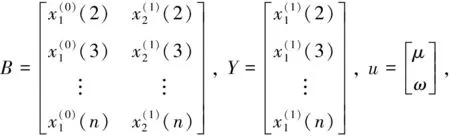
2 实证分析
本文选取4种股票(武钢股份、新五丰、大湖股份、天坛制药)的月收盘价数据(均为等时距数据)作为原始数据,如表1所示.这里,以收盘价作为主行为序列,以最高价作为影响因子序列.鉴于股票市场中过于久远的数据对未来股价预测的作用会减小,而最新的数据对预测值的影响相对较大的特点,本文选取前6个月的原始数据列来建立改进型GM(1,2)模型,并以此来预测后几个月的股票价格,其计算结果如表2所示.

表1 月收盘价原始数据
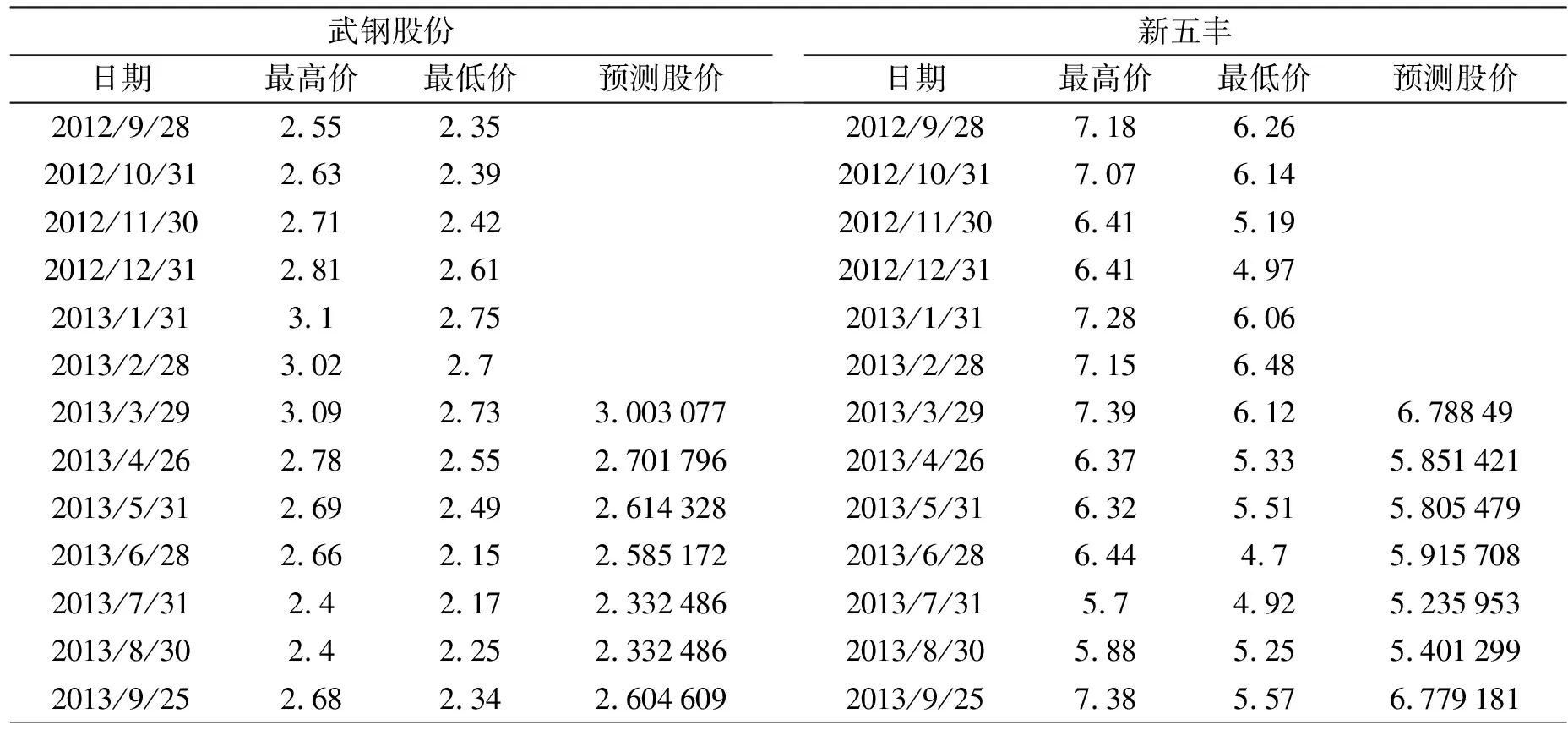
表2 2013年3月—9月预测结果
续表2

大湖股份日期最高价最低价预测股价天坛制药日期最高价最低价预测股价2012/9/287.085.702012/9/2814.7713.152012/10/316.625.872012/10/3113.8912.132012/11/306.355.212012/11/3013.3511.112012/12/317.425.132012/12/3112.4810.762013/1/317.036.252013/1/3115.5012.162013/2/286.926.302013/2/2816.2313.312013/3/297.105.716.40812013/3/2918.5015.4717.440582013/4/268.006.767.220352013/4/2619.0815.3817.987112013/5/317.947.107.1661942013/5/3118.1316.1517.09152013/6/287.415.456.6878462013/6/2817.9712.7816.940662013/7/316.555.675.9116592013/7/3116.9613.2615.988512013/8/307.036.056.344882013/8/3019.0716.4117.977652013/9/257.546.636.8051772013/9/2518.2616.3517.21405
从后几个月的预测数据可以看出,4种股票的预测价格均介于同期的实际最高价和最低价之间,这说明该模型提供的计算方法适用于股票价格的预测.在实际应用中,传统的GM(1,1)模型仅从主行为数据序列本身去寻找数据变化规律,没有考虑其它信息对主行为的影响,因此精度相对较低.而GM(1,2)模型考虑股票最高价对收盘价的影响,建立未来股票价格与收盘价的关系,获得了较好的预测效果.该模型可以用来进行短期、中期以及长期股票收盘价的分析,能更好地实施风险防范,可为投资者提供有益参考.
参考文献:
[1] 吴晓求.证券投资分析[M].北京:中国人民大学出版社,2002,8:138-144.
[2] 姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社,2003:1-347.
[3] 宋剑峰.净资产倍率、市盈率与公司的成长性:来自中国股市的经济证据[J].经济研究,2000(8):36-45.
[4] 邓聚龙.灰色系统基本方法[M].武汉:华中科技大学出版社,2005:26-74.
[5] 邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990:33-378.
[6] 王义闹,刘光珍,刘开第.GM(1,1)的一种逐步优化直接建模方法[J].系统工程理论与实践,2000,20(9):99-105.
[7] 李玻,魏勇.优化灰导数后的新GM(1,1)模型[J].系统工程理论与实践,2009,29(2):100-105.
[8] 王义闹,李应川,陈绵云.一种逐步优化灰导数背景值的GM(1,1)建模方法[J].系统工程与电子技术,2001,23(7):76-78.
[9] 王义闹,李万庆,王本玉,等.一种逐步优化灰导数白化值的GM(1,1)建模方法[J].系统工程理论与实践,2002,22(9):128-131.
[10] 张怡,魏勇,熊常伟.灰色模型GM(1,1)的一种新优化方法[J].系统工程理论与实践,2007,4(4):141-146.
[11] 党耀国,刘思峰,刘斌.以x(1)(n)为初始条件的GM模型[J].中国管理科学,2005(1):132-134.
