稀疏网格配置法在随机Burgers’方程中的应用

蔡国宪， 李炯天， 朴光日, 金元峰

( 1.韩国亚洲大学 数学系， 水原 443-749； 2.延边大学理学院 数学系， 吉林 延吉 133002 )

许多物理问题存在各种不确定性,其中的量化不确定性包括动荡、气候学、湍流燃烧、多孔介质流和流体力学等领域.不确定性的数值模拟对研究随机微分方程具有重要意义，其研究方法一般采用蒙特卡罗方法和随机Galerkin方法，然而这两种方法在模拟多维的随机非线性方程时需解决大量成本的问题；因此，提高计算精度和效率对研究更多的随机非线性方程问题有着重要意义.本文利用蒙特卡罗方法和随机稀疏网格配置法对随机Burgers’方程进行考察，验证了随机稀疏网格配置法在计算效率和精度上的优势.

1 随机配置方法

定义1(Ω,F,P )为概率空间，其中Ω为样本空间, F为样本空间Ω子集上的σ-代数， P为F上的概率测度.

考虑对于随机变量η∶Ω→R的确定函数f∶R→R.显然，f满足f(ω)=f(η(ω)).

u(z;0,t)=a(z;t),u(z;1,t)=b(z;t),u(z;x)=c(z;x).

为了求时间和空间点对于概率空间的平均和方差，首先利用一维Lagrange内插式得出关系式(1)：

(1)

这里M为配置点的个数.利用(1)式可以得出如下的一维随机函数uh,p(z;x,t)在概率空间上的平均和方差的近似值：

(2)

(3)

其中ωi表示对应的Gauss积分点zi的权重.

2 全张量积(TP)插值法

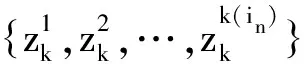
上式中zk方向的多项式次数为k(in)-1.

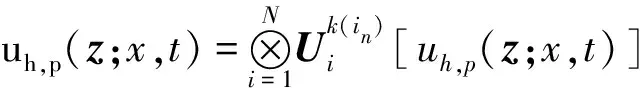
(4)

3 稀疏网格配置法

稀疏网格配置方法是由俄罗斯数学家Smolyak[4]于1963年提出的，它是一种多变量问题的数值离散方法，可有效求解多维积分[3-6].

(5)

对于d维的函数g， Smolyak’s方法可由式子

(6)

得到，其中l∈N，k∈Nd.

由(6)式可得出全张量积稀疏网格配置式：

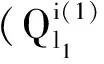
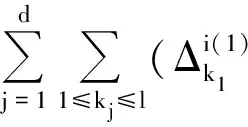
(7)

其中k满足|k|∞=max{kj}≤l和|k|1≤l+d-1.利用(5)式和(6)式可得出[7-8]:

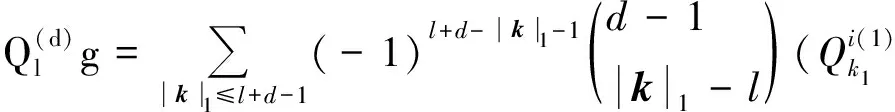
图1和图2是用Clenshaw-Curtis方法[9]得到的全张量积(TP)插值法和稀疏网格配置法的二维配置点.

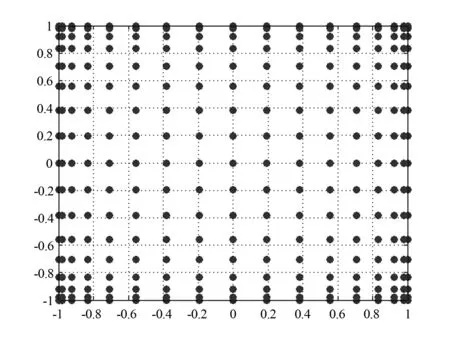
图1 全张量积插值配置点

图2 嵌套式稀疏网格配置点

4 实验结果

本文考虑如下的随机Burgers’方程：

u(ξ;0,t)=1+0.2ξ1,u(ξ;1,t)=-1-0.2ξ2,u(ξ;1,0)=-2-0.2(ξ1+ξ2)x+1+0.2ξ1，

υ=0.01, Δt=0.1, Δx=1/80,T=1，ξ1,ξ2∈U (0,1).

(8)

利用二维随机变量的稀疏网格配置法计算(8)式解的均值和方差.图3和图4是在时间T=1时(8)式解的均值和方差,其中L2、L4和L6分别表示稀疏网格配置法的级别.图5是x轴采样点和y轴误差的关系，其中‘+ - - +’折线显示蒙特卡罗方法的采样点与解的收敛关系，‘0- -0’折线显示蒙特卡罗方法取104个采样点时的解与稀疏网格配置法在不同级别解的关系，‘△- -△’折线显示稀疏网格配置法在临近的级别之间误差的减少趋势.

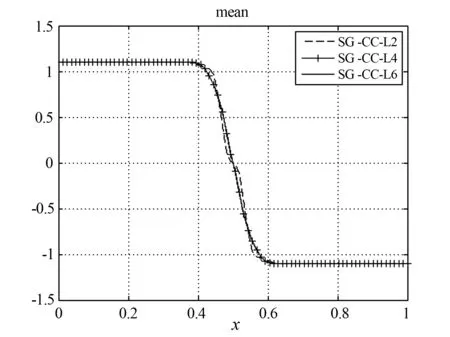
图3 时间T=1时(8)式解的平均

图4 时间T=1时(8)式解的方差

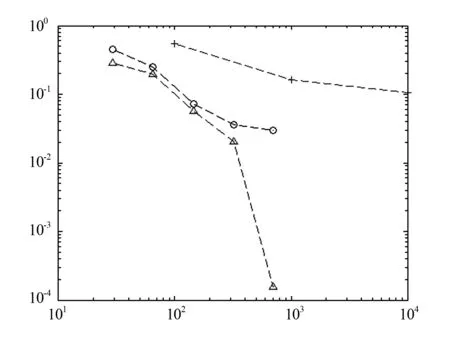
图5 误差的比较

实验结果(图5)表明：在计算精度上，稀疏网格配置法的收敛速度明显优于蒙特卡罗方法，因此可以说明稀疏网格配置法在求解随机Burger’s方程方面具有可行性.表1和表2中给出的是用蒙特卡罗方法和稀疏网格配置法的计算时间(所用计算机为win 7, Intel i 7 2.93 GHz， 8 GB内存).由表1和表2可以看出，蒙特卡罗方法取10 000个采样点时需要722 s，而稀疏网格配置法到第6个级别只需要23 s.从图3和图4可以看出,稀疏网格配置法在第6个级别已经很接近蒙特卡罗方法取10 000个采样点时的结果.由此表明，嵌套式稀疏网络配置法的计算精度以及计算效率比蒙特卡罗方法有很大的提高.

表1 蒙特卡罗方法的计算时间

表2 嵌套式稀疏网格配置法的计算时间

参考文献：

[1] Breiman L. Probability[M]. Boston： Addison-Wesley, 1968.

[2] Babuska I M, Nobile F, Tempone R. RAGS: A stochastic collocation method for elliptic partial differential equations with random input data. echnical report[J]. Siam J Numeri Anal, 2007,45(3):1005-1034.

[3] Barthelmann V, Novak E, Ritter K. RAGS: High dimensional polynomial interpolation on sparse grids[J]. Adv Comput Math, 2000,12(4):273-288.

[5] Gerstner T, Griebel M. RAGS: Numerical integration using sparse grids[J]. Numer Algorithms, 1998,18(3/4):209-232.

[6] Winckel G. RAGS: Fast Clenshaw-Curtis quadrature[J]. The Mathworks Central File Exchange, 2005.2. http://www.mathworks.com/matlabcentral/files/6911/clencurtom.

[7] Keese A, Matthies H. RAGS: Numerical methods and smolyak quadrature for nonlinear[J]. Partial Differential Equations: Informatikbericht, 2003,5:253-258.

[8] Smolyak S A. RAGS: Quadrature and interpolation formulas for tensor products of certain classes of functions[J]. Soviet Mathematics, 1963,4:240-243.

[9] Bungartz H, Griebel M. Sparse grids[J]. Acta Numerica, 2004,13:147-269.