一类单部件可修复系统的稳定性及可靠性分析
2014-03-25刘东旭司文艺袁玉娇
刘东旭, 司文艺, 袁玉娇
( 1.延边大学理学院 数学系; 2.延边教育出版社 网络出版中心: 吉林 延吉 133000 )

1 模型描述
单部件可修复系统由一个部件构成,当部件工作时系统工作,当部件故障时系统故障.当修复率为函数时,利用文献[5]中的补充变量法,单部件可修复系统的模型可用如下方程组描述:
(1)
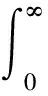
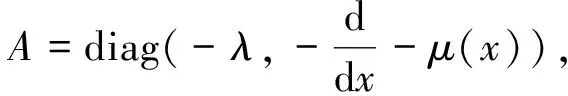
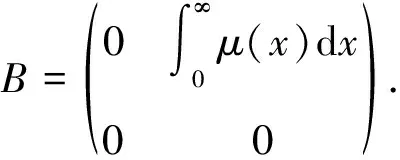
(2)
2 系统解的稳定性

定理1系统(2)存在唯一的非负解P(t), 且P(t)=T(t)P(0).
下面证明系统的解具有指数稳定性.
定理20是算子A+B的简单本征值.
证明考虑方程(γI-A-B)P=0, 即

(3)
(4)
(5)

定理3{γ∈C|Reγ>0或γ=ia,a∈R,a≠0}⊂ρ(A+B).
证明对∀γ∈C, Reγ>0或γ=ia,a∈R,a≠0有:
(6)




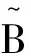

1)γ∈C, Reγ+c>0时,γ∈σ(A+B) ⟺D(γ)=0.
2)设γ0=0, 对任意的γk∈{γ∈C|Reγ>-c,D(γ)=0},γk≠γ0.其中γk按照实部递减排序Reγk+1≤Reγk,k=1,2,3,…,N, 则γ0=0是A+B的严格占优本征值.
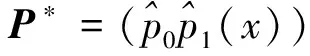
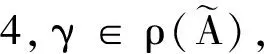
2)易知D(γ)在Reγ>-c上是解析函数,至多有有限个零点,且在有限区域内没有聚点.由上面的讨论知:算子A+B的谱在左半平面,虚轴上的点除零点外都在预解集中.因0是A+B的具有正本征向量的简单本征值,再由严格占优本征值的定义知0是严格占优本征值.
设γ0=0, 对任意的γk∈{γ∈C|Reγ>-c,D(γ)=0},γk≠γ0.其中γk按照实部递减排序Reγk+1≤Reγk,k=1,2,…,N, 则γ0=0是A+B的严格占优本征值.

‖T(t)P(0)-〈P(0),Q〉P*‖≤Me(Reγ1+δ)t,t>0.
上述结果表明,在一定条件下系统的动态解是以指数形式收敛于系统的稳态解.
3 系统的可靠性分析

定理6当0 对p0(t)求导得 参考文献: [1] Wang Wendai, Keceioglu Dimitri B. Confidence limits on the inherent availability of equipment[C]//2000 Proceedings Annual Reliability and Mainability Symposium, 2000:162-168. [2] Ananda M M A, Gamage J. On steady state availability of system with lognormal repair time[J]. Applied Mathematics and Computation, 2004,150:409-416. [3] Ananda M M A. Confidence intervals for steady state availability of a system with exponential operating time and lognormal repair time[J]. Applied Mathematics and Computation, 2003,137:499-509. [4] Chandrasekar P, Natarajan R. Confidence limit for steady state availability of systems with lognormal operating time and inverse Gaussian repair time[J]. Microelectron Reliab, 1997,37(6):969-971. [5] 曹晋华,程侃.可靠性数学引论[M].北京:高等教育出版社,2006. [6] Pazy A. Semigroups of linear operators and application to partial differential equations[M]. New York: Springer, 1983:13-22. [7] Liu Dongxu, Jin Aidong, Zhang Yufeng. Exponential stability of a four-state system[J]. Journal of Information and Decision Science, 2009,4(1):75-82. [8] 许跟起.强连续半群本质谱半径的扰动定理[J].数学学报,1990,33(6):757-763. [9] 许跟起.强连续(C0)半群扰动本质谱半径的估计[J].数学学报,1993,36(3):335-340.