基于terminal滑模与控制分配的飞翼布局无人机姿态控制

谭健, 周洲, 祝小平, 徐明兴

(1.西北工业大学 无人机特种技术重点实验室, 陕西 西安 710065;2.西北工业大学 无人机研究所, 陕西 西安 710065)

飞翼布局无人机具有气动力效率高、升阻比大、隐身性能好,续航时间长,而且载荷分布相对均匀,是高空长航时无人机的理想布局形式。同时也具有纵向弱稳定、航向中性稳定、横航向运动耦合强以及采用冗余的多操纵面配置、各操纵面存在多轴操纵耦合效应、附加力效应显著、舵效非线性等特殊问题。而且在飞行中存在风场扰动时,会带来气动力和力矩的不确定,这些特殊的问题都给飞行控制系统提出了新的挑战。需要研究干扰抑制能力强的控制方法以及在多操纵面飞翼布局无人机的飞行控制系统中引入控制分配环节,实时地将控制律所要求的操纵力矩分配给相关的操纵面[1]。

滑模变结构控制是一种设计简单,易于实现,鲁棒性强的非线性控制方法[2]。terminal滑模控制在滑动超平面设计中引入了非线性函数,使得在滑模面上跟踪误差能够在有限时间内收敛到零[3]。为了确定切换增益以满足滑模到达条件,需要事先知道干扰不确定性的信息。对此,有关学者提出了自适应滑模控制方法。但是,现有自适应滑模控制还存在着过度适应问题。自适应算法所得到的切换增益远远大于控制所需值[4]。同时为了削弱控制信号的抖振,传统的terminal滑模控制器采用饱和函数代替符号函数,存在干扰时,系统的轨迹只能渐近收敛到滑模面的邻域[5],滑模控制的连续化削弱了其鲁棒性。本文将扩张状态观测器与传统基于饱和函数的terminal滑模控制器相结合,以解决自适应terminal滑模的过度适应以及采用饱和函数对系统鲁棒性的削弱等问题。

对于控制分配,现有的研究主要有以下几种:广义逆方法、直接分配方法、线性规划和二次规划方法、动态控制分配方法等。这些方法基本上都基于伪控制指令与广义操纵面偏转角度之间呈线性关系这一假设[6],对于采用多操纵面配置、操纵面舵效非线性的飞翼布局无人机,这些方法不可避免地会产生误差,而且不能充分利用冗余操纵面,实现不同飞行条件和任务下对多种目标的综合权衡分配。因此,本文将研究一种适用于解决多操纵面飞翼布局无人机控制分配问题的多目标非线性控制分配方法。

1 飞翼布局无人机姿态模型

本文所研究的飞翼布局无人机如图1所示,其操纵面配置为4组8个操纵面。其中舵1为升降舵,舵2舵3为升降副翼,舵4为开裂式方向舵。

图1 飞翼布局无人机操纵面配置

采用开裂式方向舵等新型操纵面的飞翼布局无人机的舵偏角与期望操纵力矩向量呈非线性的映射关系,约束条件如下:

(1)

飞翼布局无人机姿态模型为如下包含不确定项的非线性系统:

(2)

(3)

飞机的姿态模型是一个典型的奇异摄动系统,将控制器的设计分为3个部分:①设计外回路控制器,用于产生内回路的控制指令；②设计内回路控制器,用于产生滚转、俯仰以及偏航控制力矩；③非线性控制分配,采用非线性规划的方法,将力矩分配到舵面上。

2 terminal滑模姿态控制器设计

2.1 内、外回路滑模面设计

选取如下terminal滑模面函数

(4)

(5)

其中ai=diag(ai1,ai2,ai3),bi=diag(bi1,bi2,bi3)(i=1,2)且aij>0,bij>0(j=1,2,3)(为减小超调现象,aij、bij取值应比较小)。如果在有限时间内系统的运动能够进入滑动模态,即系统的解满足si=0,由于terminal滑动超平面的设计中引入了非线性函数,则在滑模面上跟踪误差能够在有限时间内收敛到零。

为了使系统动态有限时间趋近滑模面,定义趋近率如下:

(6)

(7)

(εi1,εi2,εi3),Ki=diag(Ki1,Ki2,Ki3)(i=1,2)。

为了保证快速趋近的同时削弱抖振,应在增大K的同时减小ε,调节Ki和εi得到合理的趋近率。

2.2 外回路terminal滑模控制设计

对(5)式求导,代入(3)式、(7)式得到:

(8)

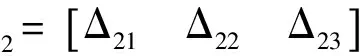
首先令Δ2=0,则根据(8)式可得外回路的名义滑模控制律为

(9)

(j=1,2,3)

(10)

于是,外回路的名义滑模控制律(9)式变为

(11)

采用饱和函数sat(s2,c2)虽然可以消除抖振,但也会带来不利的因素。当不存在干扰时,即Δ2=0,系统轨迹将渐近收敛到滑模面。当存在干扰Δ2≠0时,对每个通道,系统的轨迹将渐近收敛到滑模面的邻域|s2j|<σj,且σj满足σj=dj/(K2j+ε2j/b2j)(j=1,2,3)[5]。

由此可知,当存在干扰时,采用饱和函数sat(s2,c2),滑模控制的连续化削弱了其鲁棒性。考虑到未知不确定性Δ2的存在,本文在名义控制律(11)式的基础上,增加如下的扰动控制量:

(12)

式中：z2为外回路扩张状态观测器对干扰的估计。

此时外回路的控制量变为

x1c=-x1d+x1nor

(13)

本文采用扩张状态观测器来实现对干扰的估计。对于飞翼布局无人机姿态动力学内外环统一写成如下形式系统

(14)

(15)

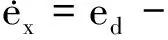
(16)

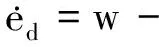
(17)

式中：ex为状态估计误差,ed为扰动估计误差。

文献[7]用自稳定域方法证明了二阶扩张状态观测器的误差方程(16)式、(17)式的状态轨线将以有限时间收敛到原点。

当误差方程(16)式、(17)式到达稳态时

ed-β1ex=w-β2fal=0

(18)

由此误差系统的稳态误差为:

ex=(w/β2)1/a, ed=β1(w/β2)1/a

(19)

可见β2取较大值时扩张状态观测器的稳态误差趋近于零。

综上所述,得到系统外回路的控制律为:

定理1 在有界干扰存在的情况下,采用如(19)式所示的基于扩张状态观测器的terminal滑模控制律时,外回路闭环是渐近稳定的。

证明:取Lyapunov函数

(20)

(21)

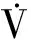
(22)

因此系统是渐近稳定的。

内环控制器形式与外环类似,在此不再赘述。

3 飞翼布局无人机的多目标非线性控制分配

采用开裂式方向舵等新型操纵面的飞翼布局无人机的舵偏角与期望操纵力矩向量呈非线性的映射关系,约束条件如下:

(23)

飞翼布局无人机在不同飞行任务阶段,往往对于控制分配具有不同的优化目标,常见的优化目标有最小能量、最小阻力、最大升力、最小雷达反射截面积[8]。

飞翼布局无人机的多目标控制分配的优化目标可描述如下:

(24)

式中:Ji为第i个优化目标,ωi为优化目标加权系数,表征每个优化目标的重要程度,将该系数按照相应物理意义赋值,可以达到实现多种任务优化目标的目的,优化目标随着任务的改变而不同,满足下式:

(25)

由于飞翼布局无人机的开裂式方向舵的偏转会产生较大的附加阻力,而飞翼布局无人机的升降副翼对升力影响比较大,当飞翼布局无人机执行常规飞行任务时,适合采用附加阻力最小的优化目标,其所需的发动机推力较小;当飞机需要快速爬升时,则可采用附加升力最大的优化目标。本文兼顾飞翼布局无人机对附加升力和附加阻力的要求,以飞翼布局无人机跟踪控制指令时附加升力较大同时附加阻力较小作为优化目标。

J=0.2(-JLift)+0.8JDrag

(26)

本文的多目标非线性控制分配采用非线性规划方法进行求解。

4 数值仿真

4.1 仿真参数设定

飞翼布局无人机的初始状态为速度0.6Ma的平飞状态,α0=1.8°,β0=0°,μ0=0°,p0=q0=r0=0 rad/s从零时刻开始,x,y,z方向分别有尺度d=530 m,强度为分别为12 m/s、10 m/s、8 m/s的突风。飞翼布局无人机的不确定环境设为:

气动力扰动为[ΔLΔDΔY]=[0.08sin(2t)L0.10sin(2t)D0.12sin(2t)Y]力矩扰动为

控制器参数选取如下:

扩张状态观测器内外环参数都为β1=800,β2=10 000,a=0.5,b=0.01。

目标指令为αc=6°,βc=10°,μc=0°。多目标非线性控制分配以飞翼布局无人机跟踪控制指令时附加升力较大并且附加阻力较小作为优化目标,即优化目标为:

J=0.2(-JLift)+0.8JDrag

4.2 仿真结果分析

仿真结果如图2至图5所示。在风场扰动下,飞行器的气动力和力矩系数都存在干扰,由图2可见,利用本文的基于扩张状态观测器的terminal滑模控制和多目标非线性控制分配方法仍然很好地实现了控制目标。本文考虑到未知不确定性的存在,用扩张状态观测器来实现对干扰的估计,内环各通道扰动估计如图3所示,观测的扰动与实际扰动曲线基本重合,扩张状态观测器很好地实现了对扰动的观测。

图2 迎角、侧滑角、速度滚转角跟踪曲线

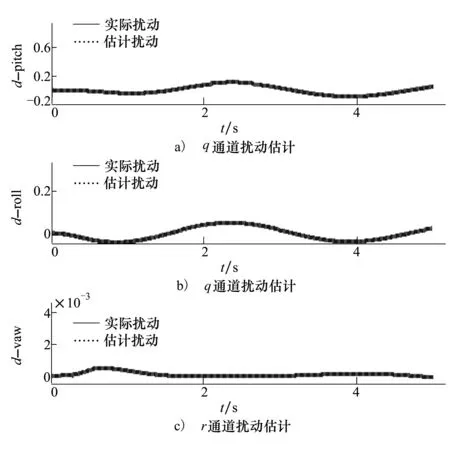
图3 内环各通道扰动的估计

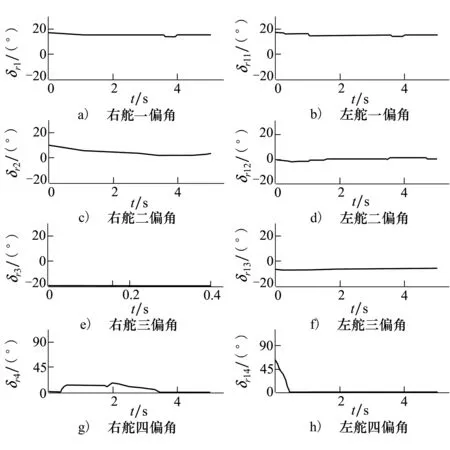
图4 飞翼布局无人机舵偏角

以飞翼布局无人机跟踪控制指令时附加升力较大且附加阻力较小作为多目标非线性控制分配的舵偏角如图4所示。

从图4可以看出,右开裂式方向舵δr4和左开裂式方向舵δl4始终只有单侧偏转。在控制分配中,开裂式方向舵可采取2种偏转方式产生偏航力矩:一种是单侧偏转;另一种是双侧独立偏转。飞翼布局无人机的开裂式方向舵的偏转会产生较大的附加阻力,产生同样的偏航力矩,采用双侧偏转会带来更大的阻力。开裂式方向舵始终单侧偏转与规划目标之一的附加阻力较小一致。采用此多目标非线性控制分配附加升力系数与阻力系数如图5所示。

图5 控制分配附加的升力系数与阻力系数

图5可看出控制分配附加升力系数为0.1左右,飞翼布局无人机在迎角为5°时机体升力系数为0.53,舵面附加升力接近无人机机体升力的20%。可见采用此多目标规划控制分配方法可以实现附加升力较大同时附加阻力较小。

综上,本文设计方案在控制的鲁棒性、精确性和快速性上具有较好的效果,控制分配时附加升力较大且附加阻力较小,实现了多目标非线性控制分配的目标,达到了设计目的。

5 结 论

1) 对飞翼布局无人机姿态控制进行分层设计,上层控制器采用基于扩张状态观测器的terminal滑模控制器,在控制的鲁棒性、精确性和快速性上具有很好的效果,底层采用多目标非线性控制分配的方法,充分利用冗余操纵面,实现对多种目标的综合权衡分配。

2) 多目标非线性规划控制分配方法能够较好地解决飞翼布局无人机的附加力效应显著、操纵面舵效非线性等问题,充分利用冗余操纵面,实现了附加升力较大的同时附加阻力较小,是一种适用于解决飞翼布局无人机控制分配问题的好方法。

参考文献：

[1] 王磊, 王立新, 贾重任. 多操纵面飞翼布局作战飞机的控制分配方法[J]. 航空学报, 2011, 32(4): 571-579

Wang Lei, Wang Lixin, Jia Zhongren. Control Allocation Method for Combat Flying Wing with Multiple Control Surfaces [J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(4): 571-579

[2] Besnard L, Shtessel Y B, Landrum B. Quadrotor Vehicle Control via Sliding Mode Controller Driven by Sliding Mode Disturbance Observer[J]. Journal of the Frankin Institude, 2012, 349(2): 658-684

[3] Chiu Chiansong. Derivative and Integral Terminal Sliding Mode Control for a Class of MIMO Nonlinear Systems[J]. Automatica, 2012, 48: 316-326

[4] 丛炳龙, 刘向东, 陈振. 刚体航天器姿态跟踪系统的自适应积分滑模控制[J]. 航空学报, 2013, 34(3): 620-628

Cong B L, Liu X D, Chen Z. Adaptive Integral Sliding Mode Control for Rigid Spacecraft Attitude Tracking[J]. Acta Aeronautica et Astronautica Sinica, 2013,34(3): 620-628 (in Chinese)

[5] 曾宪法,王洁瑶,王小虎,等. 基于SMDO的滑模控制器设计及其在导弹上的应用[J]. 航空学报, 2011, 32(5): 873-880

Zeng Xianfa, Wang Jieyao, Wang Xiaohu, et al. Design of Sliding Mode Controller Based on SMDO and Its Application to Missile Control [J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(5): 873-880 (in Chinese)

[6] 杨恩泉, 高金源, 李卫琪. 多目标非线性控制分配方法研究[J]. 航空学报, 2008, 29(4): 995-1001

Yang Enquan, Gao Jinyuan, Li Weiqi. Research on Multi-Object Nonlinear Control Allocation Method [J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(4): 995-1001 (in Chinese)

[7] Huang Yi, Han Jingqing. Analysis and Design for the Second Order Nonlinear Continuous Extended Sates Observer[J]. Chinese Science Bulletin, 2000, 45(21):1938-1944

[8] Yang L Y, Fan Y M, Shao S, et al. Control Allocation and Management of Redundant Control Effectors Based on Bases Sequenced Method[J]. Sci China Tech Sci, 2010, 53: 577-583