一种基于改进的蚁群优化算法的三维空间路径搜索算法
2014-03-25李浩宇吕梅柏
李浩宇, 吕梅柏
(西北工业大学 航天学院, 陕西 西安 710072)
蚁群优化算法 (ant colony optimization,简称ACO)是由意大利学者Dorigo等人于1991年创立,是一种启发式搜索算法。蚂蚁能在其经过的路径上释放一种特有的分泌物外激素(pheromone),使得一定范围内的其他蚂蚁能够感觉到且倾向于朝着外激素浓度高的方向移动。因此,蚁群的集体行为表现为一种信息正反馈现象,蚁群这种选择路径的过程被称之为自催化行为(autocatalytic behavior)。初步研究结果己显示出该方法在求解复杂优化问题(特别是离散优化问题)方面具有优势。
近年来随着启发式智能算法得到广泛的关注,尤其是随机搜索算法,蚁群优化算法也得到了深入发展。文献[1-2]对蚁群优化算法原理进行了详细阐述,并介绍了蚁群优化算法的各种改进方式。文献[3]将蚁群算法应用于水下自主机器人的路径规划问题,取得了很好的仿真结果。文献[4]中用MATLAB语言实现了基本的蚁群优化算法。文献[5-6]提出了一种基于梯度计算的方法将算法推广至三维或更高维数,本文在此基础上对该方法进行了改进,使得算法可以在三维空间的任意点向任意方向搜索路径,并提高了计算效率和收敛速度,并通过引入定向搜索方法解决了收敛速度慢且搜索结果不平滑的问题。
1 改进的蚁群优化算法模型
1.1 环境模型建立
本文使用栅格法[7](grid representation methods)建立环境空间模型,栅格法用大小相同的栅格划分搜索空间,并用栅格数组来表示环境,每个栅格点标以2种状态之一,在自由空间中的节点值为0,在障碍空间中节点值为1,最短路径通过搜索这张栅格地图得到。这种方法的表示效率虽然不高,但其简单性为路径规划器的实现带来了诸多方便,如表示不规则障碍物的能力,适用于大规模并行处理机实现的特点等。
1.2 符号描述与定义
由于传统的蚁群优化算法在每只蚂蚁搜索路径时对其所有的邻近点进行搜索,直至搜索到目标点,这种方法虽然可以在全域内搜索可行的路径,但是会造成收敛速度慢,路径不平滑等问题,在三维空间情况下更为严重。本文引入搜索主方向,可视域以及可行域等定义将上述问题得到了有效抑制,并应用于三维空间的搜索问题,其定义如下:
定义1 为了保证蚂蚁在搜索路径时尽量减少横向的跨越,以起始点与终点差距大的坐标轴方向为三维路径规划的主方向,其可以是横向、纵向、高度之一,记为MD。若MD为纵轴(x轴)的正方向(序号增加),则值为1,负方向值为-1;横轴(y轴)正方向值为2,负方向值为-2;竖轴(z轴)正方向值为3,负方向值为-3。若主方向上终点的坐标值大于起点的坐标值,即终点的序号大于起点的,则蚂蚁每次在主方向上前进一格(序号加1);若主方向的坐标值小于起点的,则相反。
定义2 假设MD为x轴正方向(MD=1),则对于任意一个栅格空间R中的点gi,j,k,有V(gi,j,k)∈R。可定义可视域V(gi,j,k),满足
(1)
式中:i、j、k为三维坐标轴方向上的节点序号值,r为一正整数,则称V(gi,j,k)为gi,j,k的可视域或是蚂蚁在gi,j,k处的可视域。如图1所示:
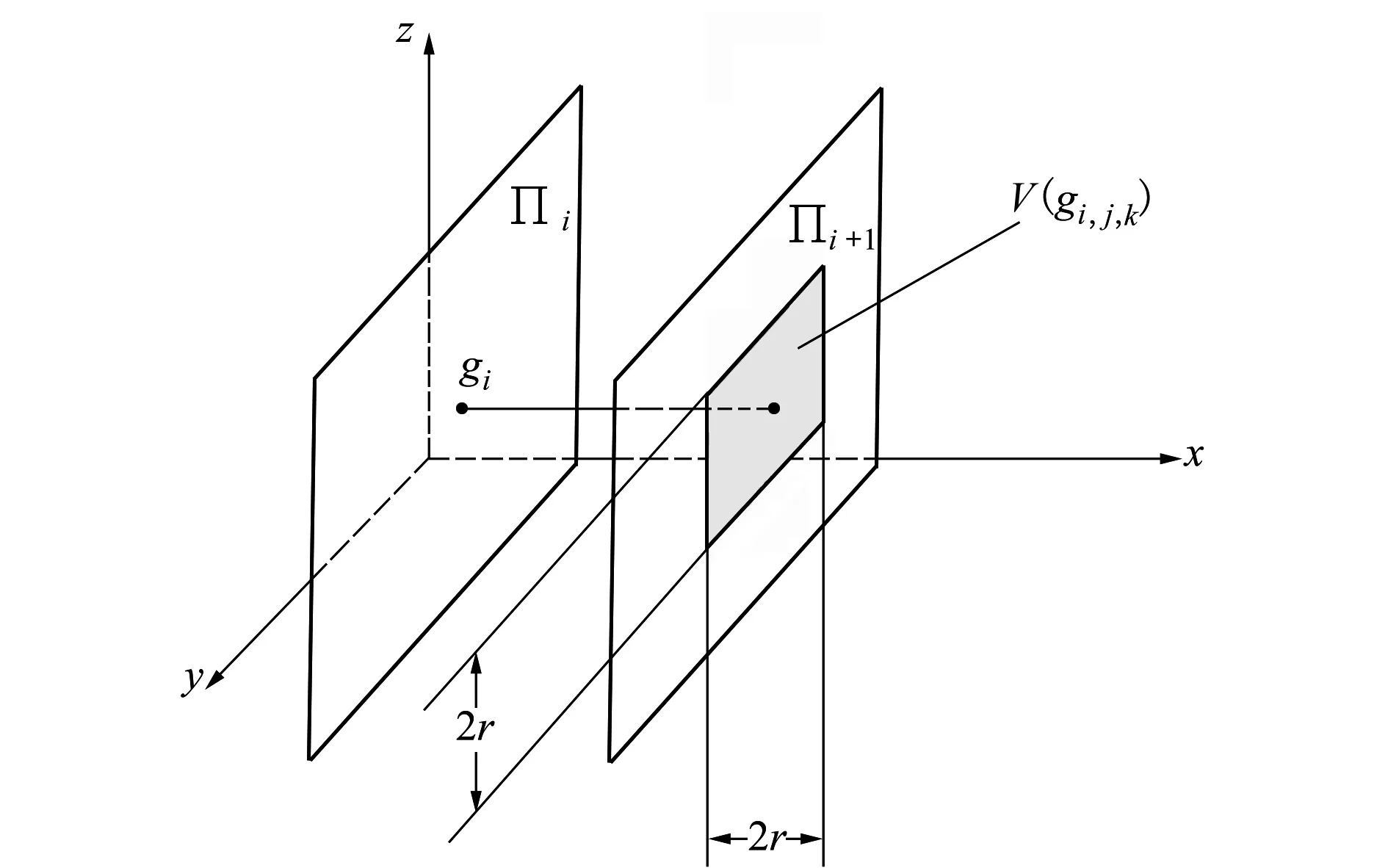
图1 可视域示意图
当可视域范围过小,蚂蚁在主方向上达到终点时,有可能由于横向移动范围不足使得蚂蚁无法到达搜索终点,所以可视域须大于某一范围,同时需保证搜索空间的连通性,这里取:
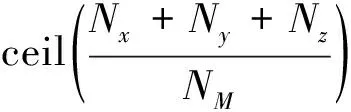
(2)
式中:Nx、Ny、Nz分别为起始点和终点之间在3个轴方向的节点个数,NM为主方向上的节点个数,ceil为向上取整函数。
定义3 设tn时刻,蚂蚁k处于g(tn),简记为gn,设此处的可视域为V(gn),则设蚂蚁k的可行后续节点集Ak(tn)={g|g∈V(gn),且g≠“1”}。
2.3 状态转移规则
设在时刻tn,蚂蚁s处在gi,j,k∈R,则对当前点的可行后续点集As(tn)中节点的选择概率计算如下:
(3)
ηi,j,k=λexp(ln,e-ln+1,e)
(4)
式中:τi,j,k为信息素值;ηi,j,k为启发函数值;α为信息素的重要程度;β为启发函数的重要程度;ln,e和ln+1,e分别为当前点和下一点距离终点的直线距离;λ为比例系数。
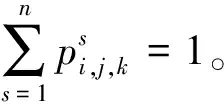
1.4 蚁群信息素更新规则
信息素矩阵τ与环境建模得到的地图矩阵相对应,每一个点的值代表相应地图上节点gi,j,k的信息素,信息素数值大表示蚂蚁经过此点的次数多。在初始化时,每一个点上的信息素值相同,均令其为1,表示信息素对选择路径点的影响都一样。
在每次迭代过程蚁群中各蚂蚁经过的点进行局部更新,目的是为了增加搜索未经过点的概率,达到全局搜索的目的,局部更新规则如下
τi,j,k=(1-ζ)τi,j,k
(5)
式中:ζ为衰减系数;τi,j,k为蚂蚁选择的后续节点。
全局信息素更新是对每次迭代中的最优路径进行更新。更新信息素矩阵中相对应最优路径节点的值,是为了将每次迭代过程中按照指标函数得到的最优路径p0,p1,…pn的节点上的值增加,从而在下次迭代中以更大的概率选择此条路径上的节点。在多次迭代之后,路径就会逐渐收敛到全局最优路径。
全局信息素更新规则如下式计算:
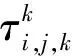
(6)

(7)
式中:ρ为挥发系数;Q为常数;τi,j,k为每次迭代中最优路径上的信息素值;fk为最优路径适应度值,一般取为路径的长度。
1.5 基于栅格法的三维空间蚁群优化算法步骤
根据定义的符号描述,基于栅格法的蚁群优化算法在三维空间的路径搜索流程如图2所示,其步骤可以总结如下:
1) 根据输入的栅格离散化地图及起始点(gsi,sj,sk)终点(gei,ej,ek)位置初始化信息素矩阵τ,给它赋一个较小正数(可取为1),计算得到MD,进化代数计数器count=0,最大进化代数为max,它标志算法的结束,每代蚂蚁总数为m;
2) k=1;
3) 如果k>m,转第7)步;否则转下一步;
4) 蚂蚁k放置在起始位置gsi,sj,sk上;
5) 计算出此时蚂蚁的Ak,若Ak为空,则宣告这只蚂蚁死亡,k=k+1,转第3)步;否则,按状态转移规则计算蚂蚁选择任意gn+1∈Ak的概率,按轮盘赌的方式选择某一gn+1,并设置此栅格点为蚂蚁k的当前位置,转第6)步;
6) 若主方向MD所表示的轴方向上,当前位置gn的下标序号与终点gei,ej,ek的下标一样(若MD等于1或-1,即x轴方向上的节点序号相同,其余主方向上以此类推),则将gei,ej,ek设为当前位置,k=k+1,转第3)步,否则转第5)步;
7) 进化代数计数器count递增1;
8) 若count>max,则算法停止,否则按信息素更新规则对蚁群信息素进行更新处理,转第2)步。
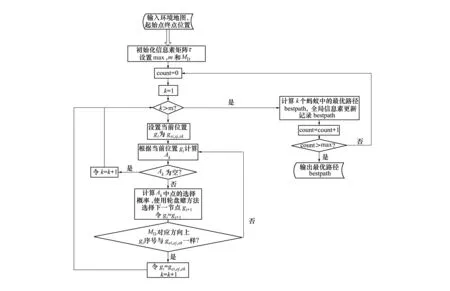
图2 改进的蚁群搜索算法流程
2 仿真结果及分析
表1规定了仿真时需要用到的一些基本搜索参数,本文后面的仿真结果均以此参数设置得出,并且均为仿真计算90次的统计值。其中信息素挥发系数ρ表示每次迭代信息素在最优路径上的挥发速度;局部信息素衰减系数ζ表示每次迭代中每只蚂蚁所选路径上的信息素衰减速度;信息素和启发函数的重要程度α和β均为1,表明两者的重要程度一样。

表1 仿真基本参数
算法模拟仿真时使用52×60×50的栅格地图模拟地形,起点坐标为(50,4,1.925),终点坐标为(3,57,2.353),由改进的蚁群优化搜索算法搜索的三维路径表示如图3所示:
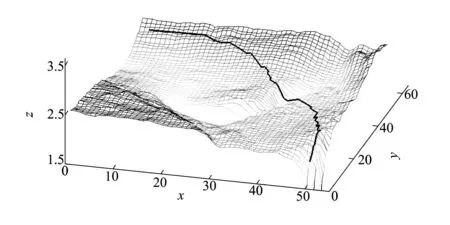
图3 路径规划结果
当选择信息素挥发系数ρ=0.2,局部衰减系数ζ=0.2而蚁群种群数量不同时,规划的路径长度随迭代次数的变化趋势如图4所示。从图中可以看出随着迭代次数的增加路径的长度趋于最优,且随着种群数量的增加改进方法的优势更加明显。图5所示为不同种群数量规划的每次迭代结果的平均方差变化趋势,从对比可以看出改进方法的平均方差远小于传统方法,且波动幅度比传统方法小,说明改进方法的稳定性明显优于传统方法。
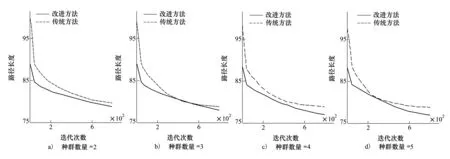
图4 改进方法与传统方法的规划结果随迭代次数变化规律
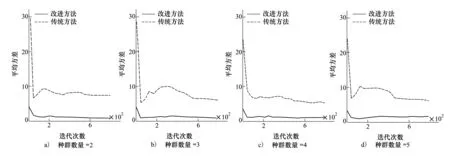
图5 改进方法与传统方法的规划结果方差的变化规律
表2为种群数量为5、ζ=0.2的情况下改进算法与传统算法时间消耗随挥发系数的变化对比关系。表3为种群数量为5、ρ=0.2的情况下改进算法与传统算法时间消耗随信息素衰减系数的变化对比关系。从表2中可以看到,由于挥发系数的引入,收敛速度变慢,使得传统方法规划时间相对变长;而改进方法的规划时间只取决于搜索起始点与终点之间的节点数,所以其规划时间基本保持不变。从表3中可以看到衰减系数的引入使得两种方法规划的路径长度都有相应的减小,平均方差增大,说明衰减系数的引入提高了算法在极值点附近的搜索能力,但降低了算法的稳定性;同时传统方法的计算时间有一定的减少。表2和表3都显示出改进的蚁群算法明显比传统算法节省计算时间,为实时规划提供了可能。
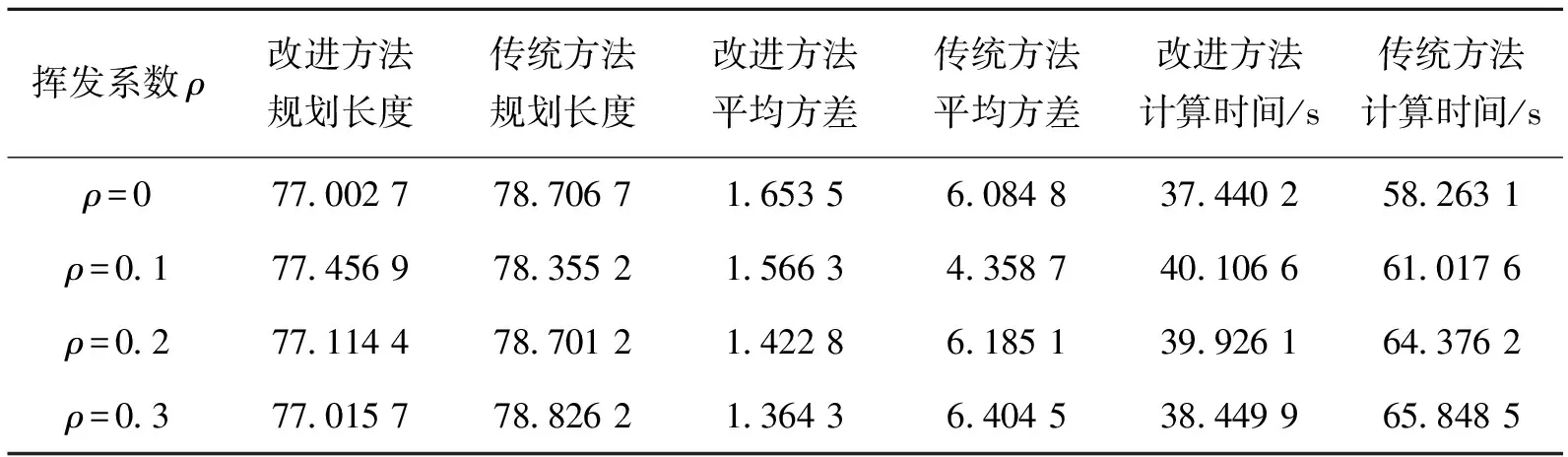
表2 规划结果随挥发系数变化规律
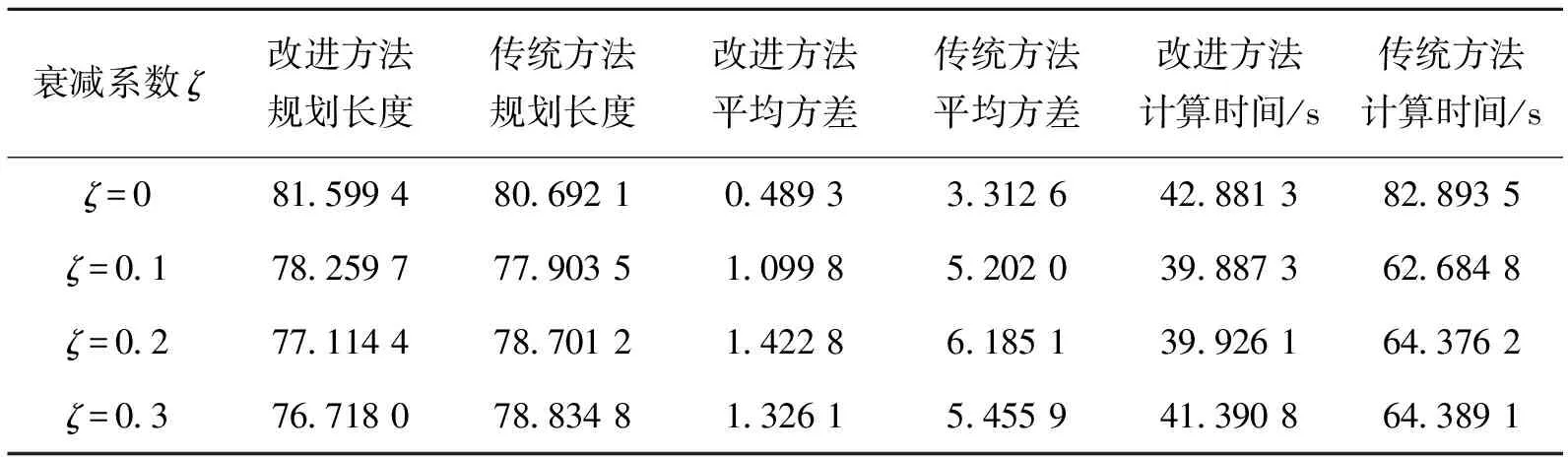
表3 规划结果随衰减系数变化规律
总体上讲,改进的蚁群算法在规划路径的长度、平均方差和计算时间上均明显比传统方法占优。
3 结 论
文中通过引入搜索主方向、可视域以及可行域等定义,将传统的二维蚁群搜索算法改进,并扩展至三维情况。并给出了算法的流程及步骤,然后通过Matlab进行了仿真分析。通过仿真得出该改进方法与传统方法相比,运行效率大大提高,收敛速度加快,具有更好的稳定性。
参考文献:
[1] Dorigo M, Stützle T. The Ant Colony Optimization Metaheuristic: Algorithms, Applications and Advances∥Handbook of Metaheuristics[M]. Glover F, Kochenberger G. MA: Kluwer, 2002
[2] 李士勇. 蚁群算法及其应用[M]. 哈尔滨:哈尔滨工业大学出版社,2004
Li Shiyong. Ant Colony Algorithms with Applications[M]. Harbin: Harbin Institute of Technology Press, 2004 (in Chinese)
[3] 伍祥红. 基于蚁群优化的自主水下机器人路径决策方法研究[D]. 哈尔滨:哈尔滨工程大学,2007
Wu Hongxiang. Research on Path Decision Making Method for AUV Based on ACO[D]. Harbin, Harbin Egineering University, 2007 (in Chinese)
[4] 史峰,王辉,胡斐,等. MATLAB智能算法30个安例分析[M]. 北京:北京航空航天大学出版社,2011:229-236
Shi Feng, Wang Hui, Hu Fei, et al. 30 Intelligent Algorithm Cases Analysis in MATLAB[M]. Beijing: Beihang University Press, 2011: 229-236 (in Chinese)
[5] Christian Blum, Marco Dorigo. The Hyper-Cube Framework for Ant Colony Optimization[J]. IEEE Trans Syst Man Cybern B, 2004, 34(2): 1161-1172
[6] Blum C, Roli A, Dorigo M. HC-ACO: the Hyper-Cube Framework for ant Colony Optimization[C]∥Proc MIC’2001——Metaheuristics Int Conf, 2001: 399-403
[7] 王晓林. 基于栅格法的仿生机器鱼路径规划研究[D]. 天津:天津大学,2010
Wang Xiaolin. Path Planning of the Biomimetic Robotic Fish Based on the Grid Method[D]. Tianjin, Tianjin University, 2010 (in Chinese)
