考虑几何非线性效应的大柔性太阳能无人机静气动弹性分析

王伟, 周洲, 祝小平, 王睿

太阳能无人机能够完成大范围、长时间的大气环境探测、军事侦查和通信中继任务,并在各国频频传出新的研究进展[1-5]。这类无人机一般具有较大的展弦比、较低的结构面密度等特点,比如“太阳神”太阳能无人机的展弦比达到31,而常规动力的高空长航时无人机“全球鹰”的展弦比为25,并且两者的机翼结构面密度分别为3.2 kg/m2和53kg/m2。太阳能无人机的大展弦比、轻质结构设计特点使其在飞行中产生明显的机翼结构静变形,如“探路者”太阳能无人机平飞时机翼上翘量超过半展长的12%,“太阳神”在极限飞行状态下的机翼上反角可达到50°[3-4]。2003年6月,加装实验设备的Helios无人机飞行时,在低空出现振荡导致全机解体坠毁。2004年1月,NASA发布的事故调查报告中提出继续研制这种无人机,并着重强调了对这种无人机非线性气动弹性特性分析方法的研究[6]。扭转变形较小时,采用线弹性结构模型模型研究静气动弹性问题,气动力随挠度的增大而单调增加,变形略大时与实际严重不符[7]。因此,这类大变形无人机的结构建模必须考虑大位移、大转角等几何非线性特征。

目前,大柔性机翼的几何非线性结构模型主要有Hodges-Dowell理论梁模型和基于Total Lagrange(TL法)、Updated Lagrange(UL法)和共旋坐标法(CR)的有限元模型。其中,在NASA的资助下,基于Hodges-Dowell非线性梁模型的高空长航时(HALE)飞机非线性气动弹性配平及稳定性计算代码(NATASHA)的开发得到了一定的发展,可以预测飞翼布局HALE飞机的气动弹性响应特性,但变形的计算需要预先求解结构内力[7-10];传统的TL法变形前后单元坐标系保持不变,无法考虑变形后结构状态的影响;UL法中单元两端坐标转换矩阵不一致,也无法考虑弯曲变形的影响;因此,这2种方法通常需要增加载荷步以提高求解精度,从而显著增加计算时间。CR有限元法是近年来发展起来的新的几何非线性计算方法,主要思想是:把结构的运动分解为纯粹的弹性变形和刚体的平移及转动,位移-应变关系建立在局部坐标系内,不像传统的TL法那样从非线性位移-应变关系出发来推导切线刚度矩阵,并且具有更高的求解精度和计算效率[11-12]。因此,本文针对大柔性太阳能无人机机翼结构的大位移、大转动、小应变特征,通过建立节点随动坐标系和单元随动坐标系,推导了基于CR有限元理论的切线刚度矩阵、内力求解格式及增量平衡方程,编写了基于CR有限元理论的几何非线性结构静力学求解代码;气动载荷在3个方向上进行积分,以描述结构大变形引起的气动载荷作用方向的改变。

1 大柔性结构几何非线性静力学建模

大柔性无人机机翼可以用柔性梁模型来描述[7-9],因此本文选择空间CR梁单元建立大柔性太阳能无人机的结构模型。采用有限元技术对大柔性结构建模时,其计算精度主要取决于刚度矩阵和坐标系转换矩阵对几何非线性描述的精确性。CR法的平衡方程在单元坐标系内建立,通过坐标转换矩阵及其微分形式构造总体坐标系下的切线刚度矩阵,因而其核心是坐标转换矩阵的建立及其微分形式的推导。

1.1 坐标系的建立

坐标转换矩阵是单元坐标系与总体坐标系之间的联系纽带,为了较精确地描述坐标系转换矩阵,本文引入总体坐标系Ixyz、节点坐标系ui、单元平均构形坐标系um和单元坐标系ue。

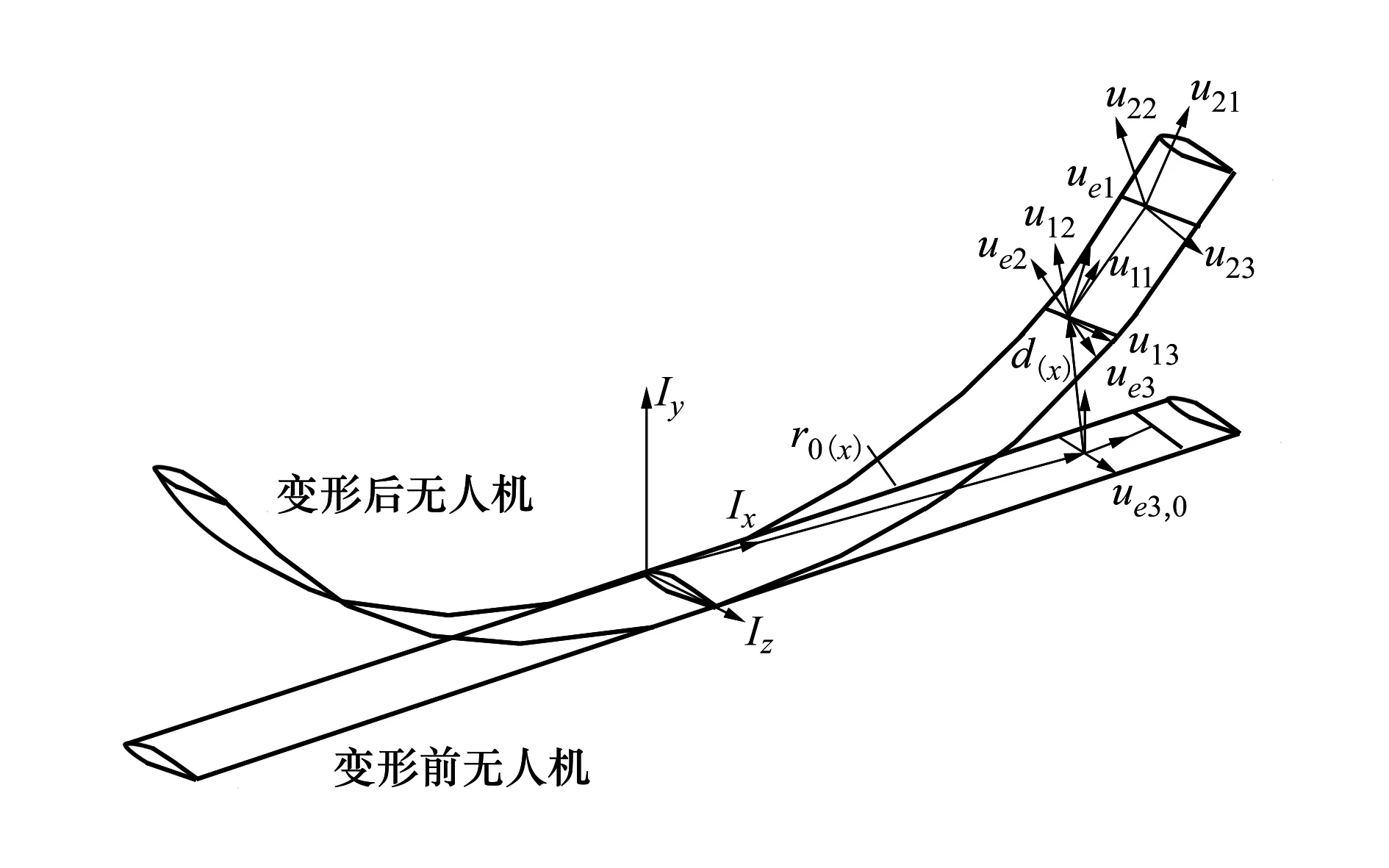
图1 柔性结构变形示意图

当结构位形确定时,单元节点的3个欧拉角及空间坐标随之确定,按照式1旋转总体坐标系可以得到节点坐标系。

ui(x)=Ti(x)Ixyz

(1)

Ti(x)是节点i的坐标系转换矩阵,是3个欧拉角φx,φy,φz的函数,其中:

对于2节点空间梁单元,采用(1)式可以得到节点坐标系ui和uj,假设其坐标转换矩阵Ti和Tj对应的旋转伪矢量为(θix,θiy,θiz)T和(θjx,θjy,θjz)T,参照文献[11],以γ/2作为旋转伪矢量,对节点坐标系ui进行旋转得到平均构形坐标系um。

um=R(γ/2)ui

(2)

式中：γ=(θjx-θix,θjy-θiy,θjz-θiz)T

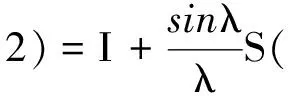
S(γ/2)S(γ/2)λ=((γ/2)(γ/2)T)1/2

I为单位阵。

S(γ/2)=

那么参照文献[11],空间梁单元的单元坐标系的定义为:

(3)

式中：d1与d2分别是节点i、j的现时坐标,ln=((d2-d1)T(d2-d1))1/2。

1.2 增量平衡方程推导

CR有限元法充分利用了几何非线性问题的小应变、大位移特征,弹性变形在单元坐标系内描述,位移-应变关系仍然是线性的。利用方程(3)建立的单元随动坐标系与方程(1)建立的节点随动坐标系,得到单元坐标系下节点的弹性变形:

(4)

对(4)式进行微分得到位移增量从单元坐标系到总体坐标系的坐标转换矩阵T:

δpl=Tδp

(5)

单元坐标系下的广义节点力fl为:

fl=Klpl

(6)

式中:Kl是线性刚度矩阵,与线性梁单元的刚度矩阵一致。

则总体坐标系下广义节点力向量f为:

(7)

(8)

TTKlT为材料刚度矩阵,KTσ(fl)为几何刚度矩阵,是单元坐标系下单元节点力fl的函数。大柔性结构几何非线性问题求解时,0,Δt,2Δt,…,t时刻的结构状态是已知的,t+Δt时刻的状态未知量是待求解的。那么,结构静力学增量平衡方程为:

KTΔp=Ft+Δt-ft

(9)

2 几何非线性静气动弹性建模

假设机翼剖面为刚性,变形后的机翼外形通过一系列控制剖面的平移和转动经过拟合得到;如图2所示,剖面i、j分别由结构节点i、j的线位移和角位移控制。流场控制方程采用三维可压N-S定常方程,湍流模型采用k-kl-ω转捩模型,流场计算采用Fluent软件。气动力在总体坐标系的3个方向分别进行积分,然后根据功互等原理,将分布的气动力载荷转换到节点上,得到等效节点力,计算公式为:

(10)

图2 气动载荷插值示意图

那么,静气动弹性运动方程为:

KTΔp=Qt-ft

(11)

收敛控制方程为:

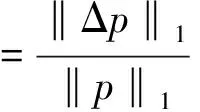
(12)

一般,前2～3次主迭代时Qt-ft较大,需要对载荷进行分步施加,以保证求解精度及收敛效率。

3 代码验证及算例分析

3.1 悬臂梁在集中弯矩下的位移求解

根据上述计算方法编制了非线性有限元求解代码,为了验证其计算精度和效率,选择具有解析解的大柔性悬臂梁作为算例。悬臂梁自由端受集中弯矩M作用,取l=20 m,EIz=10 Nm,EA=10 N,M分别取0.2π、0.4π、0.6π、0.8π和π。其解析解为弧长20 m,圆心角θ=0.4π、0.8π、1.2π、1.6π和2π的圆弧。将悬臂梁划分为20个单元,采用所述载荷增量法进行求解,收敛控制方程采用(12)式,子迭代采用Newton-Raphson迭代格式,位移增量允许误差<10-3,变形如图3所示。

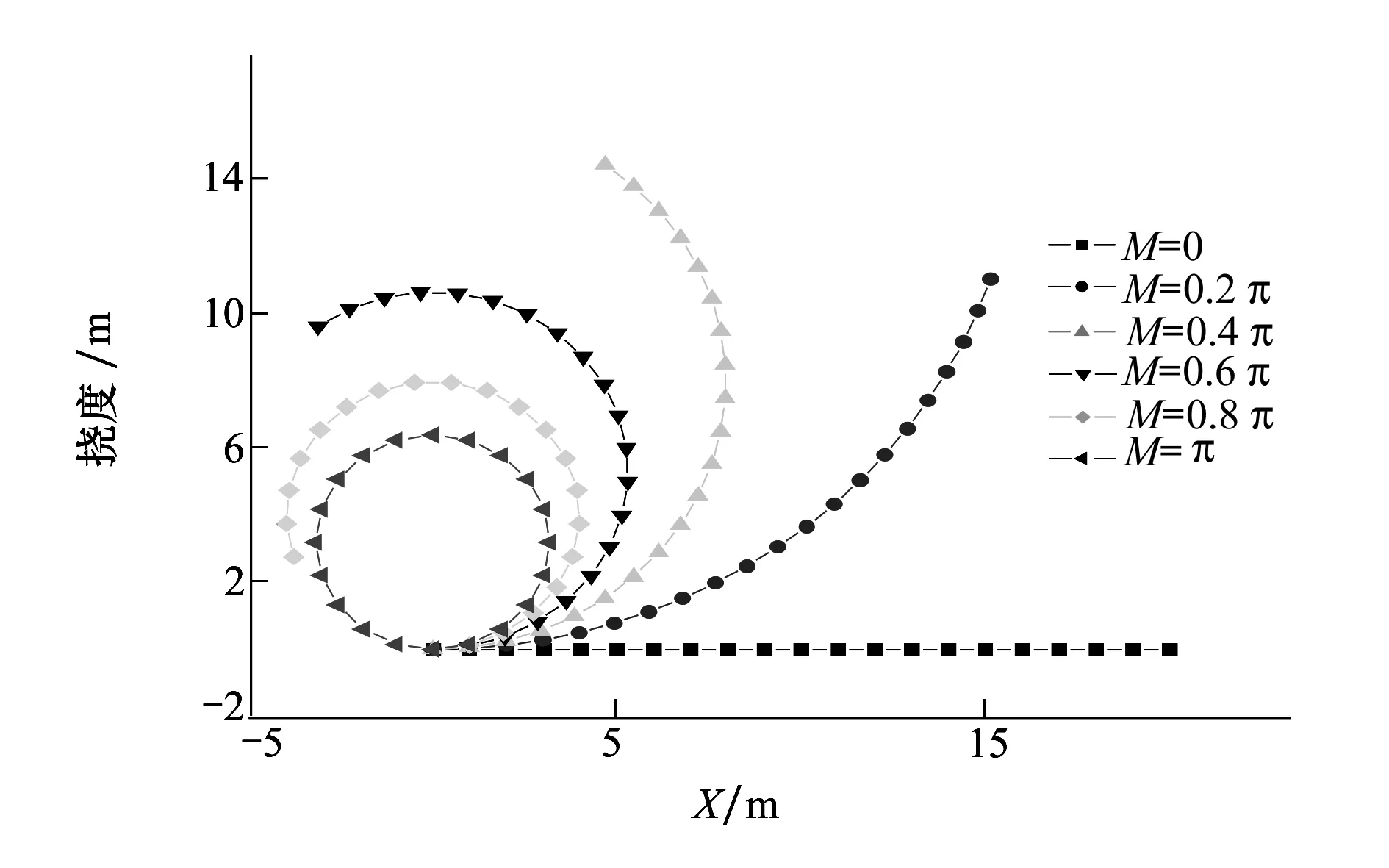
图3 悬臂梁几何大变形

上述算例求解中,子迭代经过3～4次迭代收敛,且最大误差不超过3%,可见CR有限元法具有较好的求解精度及求解效率,并且能够非常精确地模拟到结构的几何非线性变形特征。

3.2 大柔性太阳能无人机非线性静气动弹性计算与结果分析

大柔性太阳能无人机的几何参数、结构参数及飞行条件如图4及表1所示:

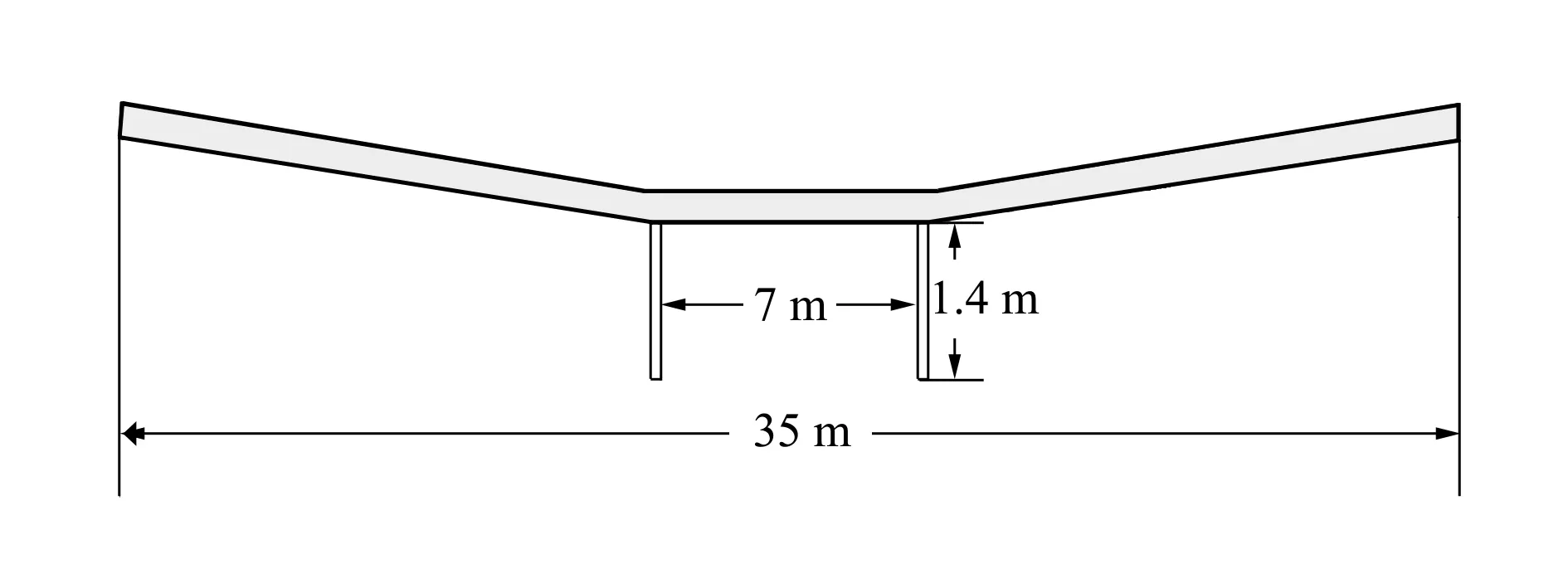
图4 太阳能无人机几何模型

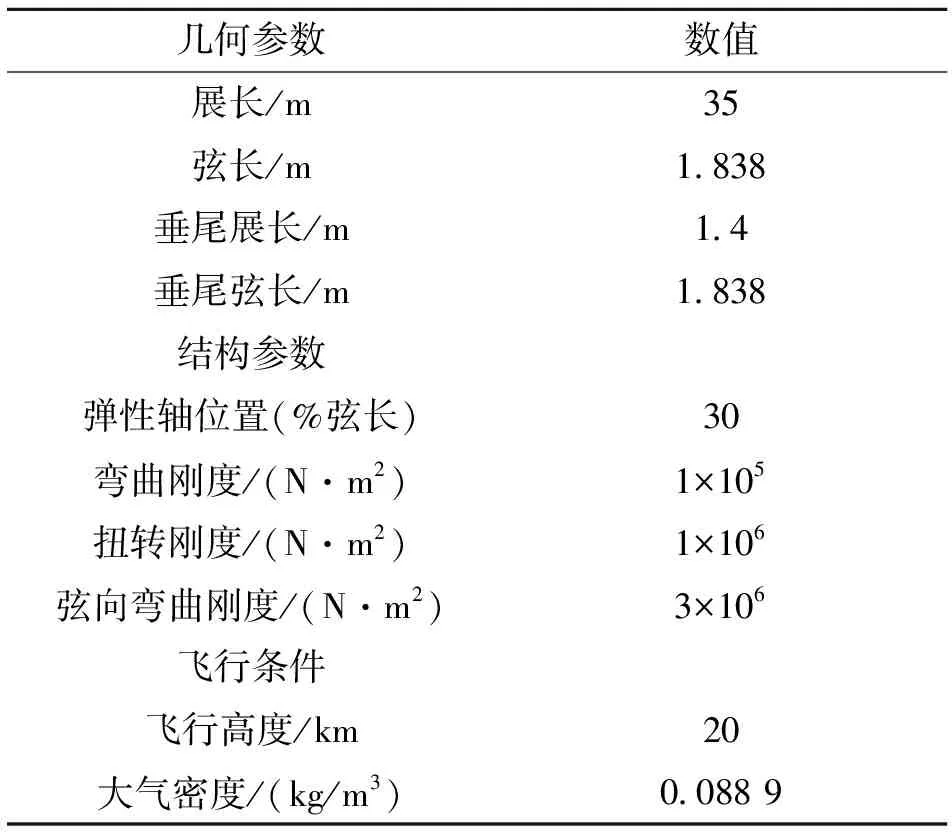
表1 太阳能无人机模型参数

以来流速度作为变化参数,气动载荷随来流速度的增加而增加,以描述结构在不同气动载荷作用下的弹性变形,随后冻结气动外形,研究该几何大变形对气动特性及横航向稳定性的影响。不同气动载荷作用下的机翼变形历程如图5所示。

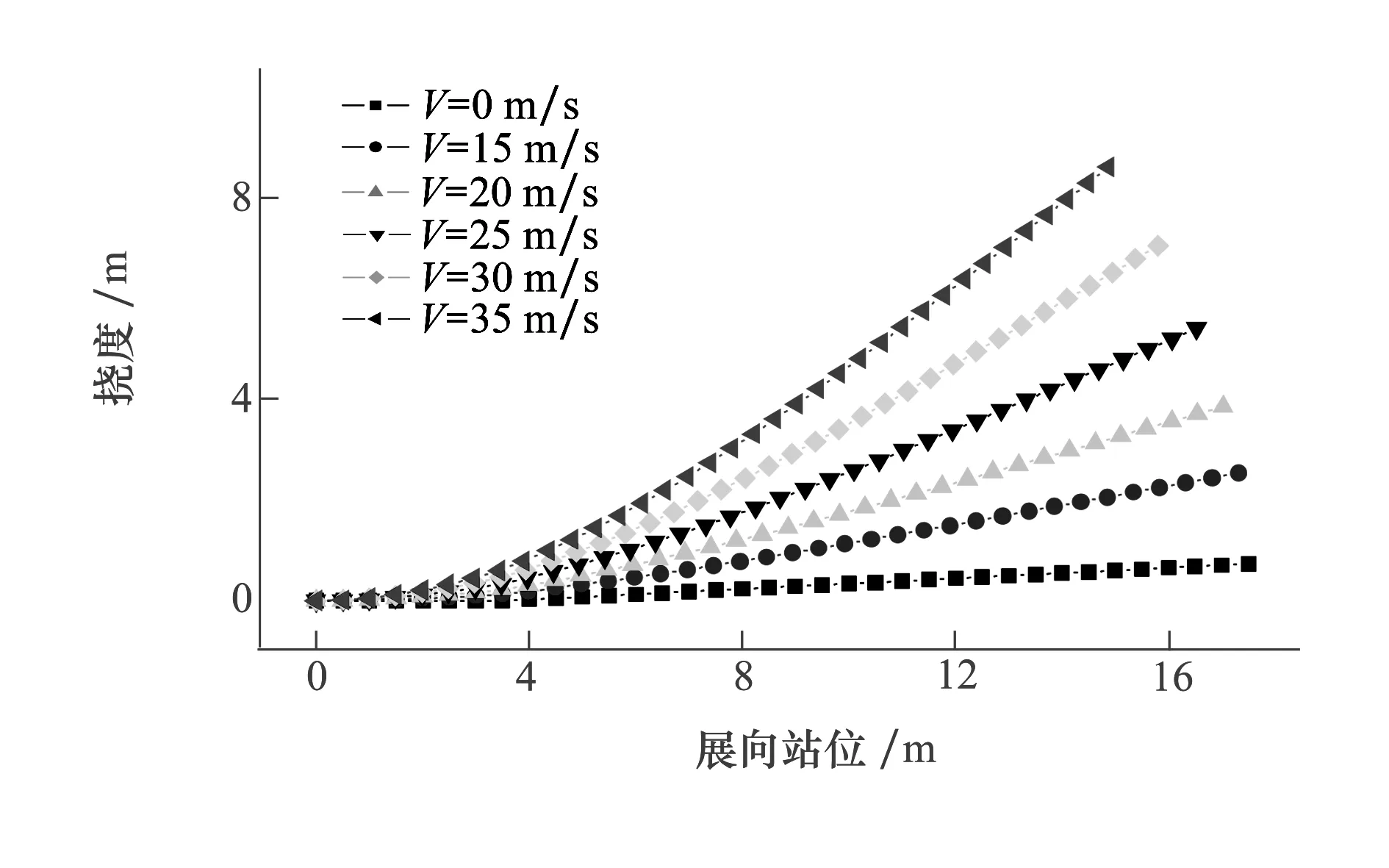
图5 不同来流速度下的机翼变形历程

来流速度V=0 m/s表示无人机初始刚体外形,V=15 m/s 、20 m/s、25 m/s、30 m/s、35 m/s时,所引起的翼尖挠度分别为展长的5%、8.9%、13.3%、18%、22.5%,引起的翼尖展向位移分别为展长的0.5%、1.3%、2.7%、4.9%,7.5%,相当于展长缩短了1%、2.6%、5.4%、9.8%,15%;另外,可以看出气动载荷作用的方向也发生了明显的变化。

机翼的弹性变形会引起载荷的重新分布。无人机在不同来流速度作用下,结构发生几何大变形时的升力重新分布情况如图6所示。当地升力系数计算时选择局部机翼面积作为参考面积,默认无人机迎角为0°。

机翼的弹性变形使气动载荷向翼根转移,这种几何非线性效应改善了机翼结构的外载荷分布,对结构设计是有利的,而线弹性结构模型无法精确地模拟到这种趋势,甚至得到相反的结论。

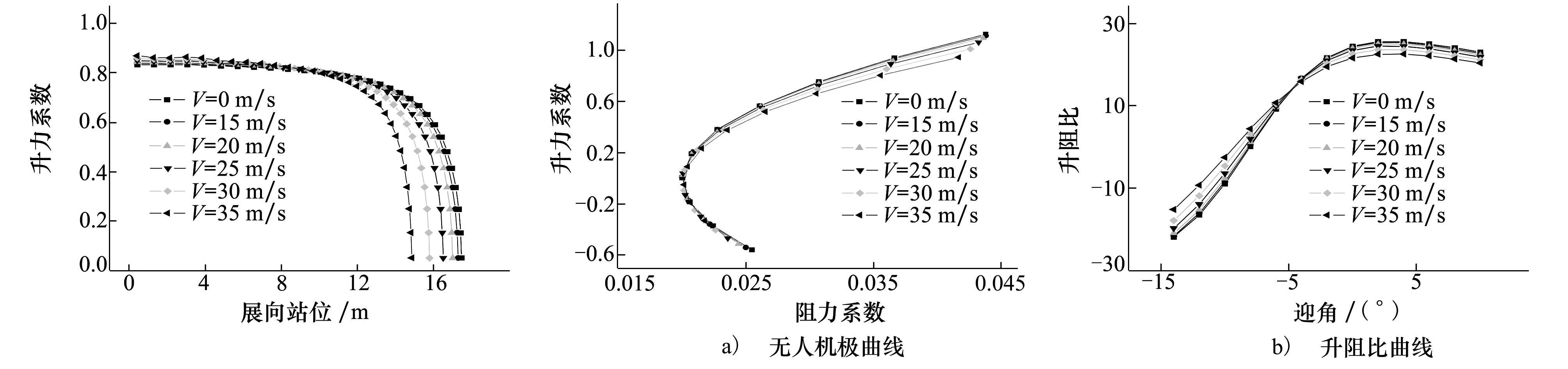
图6 升力沿展向分布 图7 无人机极曲线与升组比曲线

当翼尖挠度为22.5%的展长时,升力系数降低了12.4%,升阻比降低了11.8%。随着变形增加,阻力系数基本不变,而升力系数减小比较快,因而升阻比的变化趋势也是减小的。这主要是因为几何大变形改变了气动载荷的作用方向,对全机升力的影响较大。采用线弹性结构模型时,气动力是随弯曲变形的增加而单调增加的[7],因此采用线性结构模型与非线性结构模型研究较大弹性变形对气动力的影响时,会得到不同的结论。

太阳能无人机机翼的几何大变形相当于增加了机翼的上反角,严重影响了无人机的横航向力矩特性,如图8所示,Cl为滚转力矩系数、Cn为偏航力矩系数,Clβ和Cnβ分别是滚转力矩导数和偏航力矩导数。

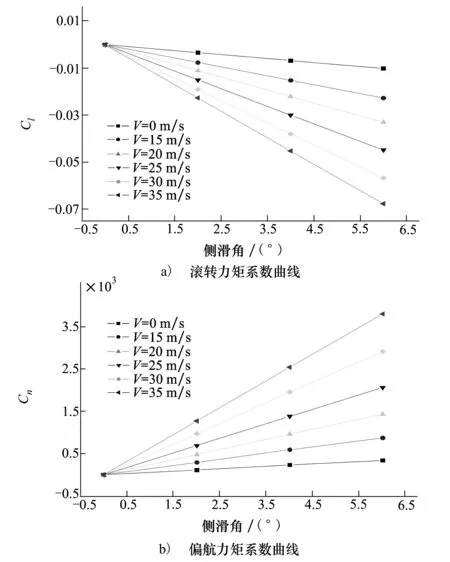
图8 横航向力矩系数

随着弹性变形的增加,Clβ和Cnβ的绝对值都呈增加趋势;从图8中还可以看出,几何非线性效应对无人机横航向稳定性的影响较大。

当弯曲变形为22.5%的展长时,滚转力矩导数为刚性飞机的6.65倍,偏航力矩导数为刚性飞机的10.3倍,Cnβ/Clβ为刚性飞机1.66倍。因此,这类飞机的大弹性变形使滚转力矩和偏航力矩得到很大提高,且显著改善了横航向静稳定性。

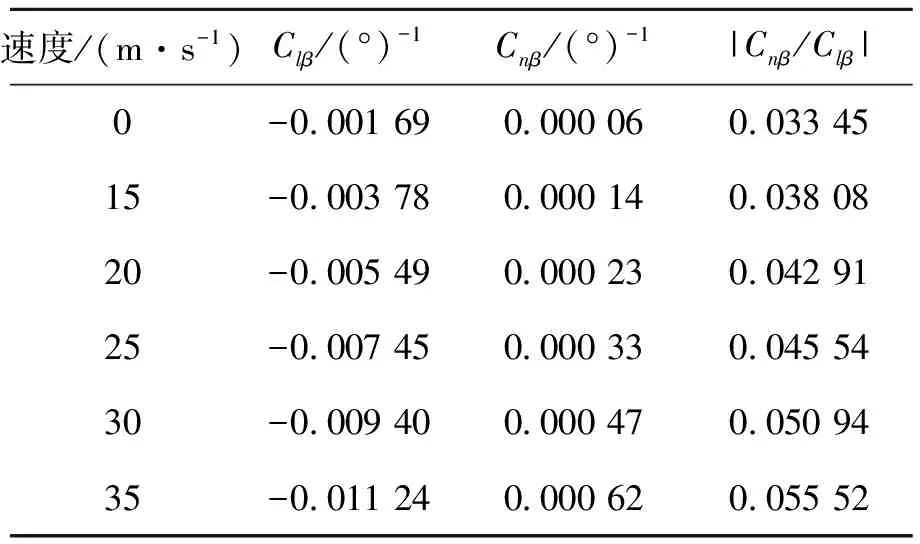
表2 横航向气动特性

4 结 论

本文结合CR有限元法及计算流体力学理论,对大柔性太阳能无人机的静气动弹性问题进行了深入的研究,得到以下结论:

1)大柔性太阳能无人机的结构建模应采用能够考虑几何非线性效应的结构模型。CR有限元法具有较好的计算精度和求解效率,能够较好地模拟大变形无人机的几何非线性特征,可以用来建立大柔性太阳能无人机较高精度的非线性结构模型。

2)几何非线性效应改善了气动载荷的重新分布,有利于机翼结构设计;但同时会降低无人机的气动性能。

3)对具有正常横航向稳定性的飞机,当Cnβ/Clβ过大时,飞机易产生螺旋不稳定;当Cnβ/Clβ过小时,则飞机易产生荷兰滚或飘摆不定,而弹性变形对Cnβ及Clβ的影响比较明显,大柔性太阳能无人机在总体设计时,应考虑几何大变形对气动特性及横航向稳定性的影响,特别是确定上反角等设计参数时。

参考文献：

[1] Cestino E. Design of Very Long-Endurance Solar Powered UAV[D]. Politecnico di Torino, 2006

[2] Romeo G, Frulla G, Cestino E, Corsino G. HELIPLAT: Design, Aerodynamic, Structural Analysis of Long-Endurance Solar-Powered Stratospheric Platform [J]. Aircr, 2004, 41(6): 1505-1520

[3] Kirk Flittie, Bob Curtin. Pathfinder Solar-Powered Aircraft Flight Performance [R]. AIAA-1998-4446

[4] Youngblood J W, Talay T A. Solar-Powered Airplane Design for Long-Endurance, High-Altitude Flight [R]. AIAA-1982-0811

[5] 昌敏,周洲,郑志成. 太阳能飞机原理及总体参数敏度分析[J]. 西北工业大学学报, 2010, 28(5):792-796

Chang Min, Zhou Zhou, Zheng Zhicheng. Flight Principles of Solar-Powered Airplane and Sensitivity Analysis of Its Conceptual Parameters[J].Journal of Northwestern Polytechnical University, 2010, 28(5):792-796 (in Chinese)

[6] Noll T E, Brown J M, Perez-Davis M E, Ishmael S D. Investigation of the Helios Prototype Aircraft Mishap[R]. Tech Rep, NASA, 2004

[7] Patil M J, Hodges D H, Cesnik C E S. Nonlinear Aeroelasticity and Flight Dynamics of High-Altitude Long-Endurance Aircraft[R]. AIAA-1999-1470

[8] Patil M J, Hodges D H. Flight Dynamics of Highly Flexible Flying Wings [R]. Journal of Aircraft, 2006, 43(6): 1790-1798

[9] Jaworski J W. Nonlinear Aeroelastic Analysis of Flexible High Aspect Ratio Wing Including Correction with Experiment[D]. Duke University, 2009

[10] Zhang Jian, Xiang Jinwu. Nonlinear Aeroelastic Response of High-Aspect-Ratio Flexible Wings[J]. Chinese Journal of Aeronautics, 2009, 22(4): 355-363

[11] Crisfield M A, Galvanetto U, Jeleniĉ G. Dynamics of 3-D Co-Rotational Beams[J]. Computational Mechanics,1997,20:507-519

[12] Rafael Palacios, Joseba Murua, Robert Cook. Structural and Aerodynamic Models in Nonlinear Flight Dynamics of Very Flexible Aircraft[J]. AIAA Journal, 2010, 48(11): 2648-2659