GNSS接收机采样率的选择及对相关器输出的影响

宋玉龙, 廉保旺

(西北工业大学 电子信息学院, 陕西 西安 710072)

大多数现代GNSS(global navigation satellite system,全球导航卫星系统)接收机是数字接收机,而开发数字接收机的首要工作就是设计采样率,它直接影响了接收机的正常工作、跟踪精度和资源利用效率。采样率的选择主要取决于中频信号形式(实/复信号)、中频频率、伪码速率及相关器间隔等。

接收机射频前端结构的不同会影响中频频率的选择,以及中频信号的形式,并决定了带通采样的策略。文献[1]对外差式、零中频、低中频等射频前端结构及混频信号频谱进行了详细的分析,并讨论了各自的优缺点。本文对GNSS数字接收机常用的外差式和低中频结构进行了研究。

在射频前端输出的中频信号基础上需要研究带通采样率的设计。Akos在文献[2-3]中研究了将射频信号用带通采样直接下变频到基带的方案,并说明了带通采样的原理及采样率的设计方法;文献[4]中详细研究了实数信号的带通采样率设计;文献[5]中详细研究了复数信号的带通采样率设计。本文研究在实/复数形式的中频信号上进行抗混叠带通采样(不利用带通采样下变频)的采样率设计。

文献[6-9]研究了采样率对环路跟踪性能的影响,均推荐采样率设计成伪码速率的非整数倍,但并没有深入研究影响跟踪性能的根本原因,也没有给出具有说服力的仿真结果。本文解决了这些问题。文献[10]给出了相关器间隔对采样率选择的影响,本文通过仿真和论证纠正了文中存在的错误。

最后本文综合考虑了信号形式、中频频率、伪码速率、相关器间隔及硬件资源等因素,给出了最优的采样率设计策略。

1 采样率与中频频率

1.1 射频前端结构

射频前端模块位于接收机天线与基带数字信号处理模块之间,它的主要目的是将接收到的射频模拟信号数字化成包含GNSS信号成分、频率较低的中频信号,并在此过程中进行必要的滤波和增益控制。卫星与接收机之间的相对运动会引起信号载波频率的多普勒效应,使接收到的卫星信号的载波频率发生偏移。因为这种相对运动状况和相应的多普勒频移量通常是不可预测的,所以射频前端只得将接收信号从射频下变频到中频(或者近基带),而不是直接下变频到真正的基带[11]。

GNSS接收机的射频前端主要采用2种结构,一种是经典的外差式接收机结构,如图1所示;另一种是近来各接收机厂商常使用的低中频结构,如图2

所示。2种结构在对中频频率的选择以及之后的A/D采样方面都有着不同的处理方案。

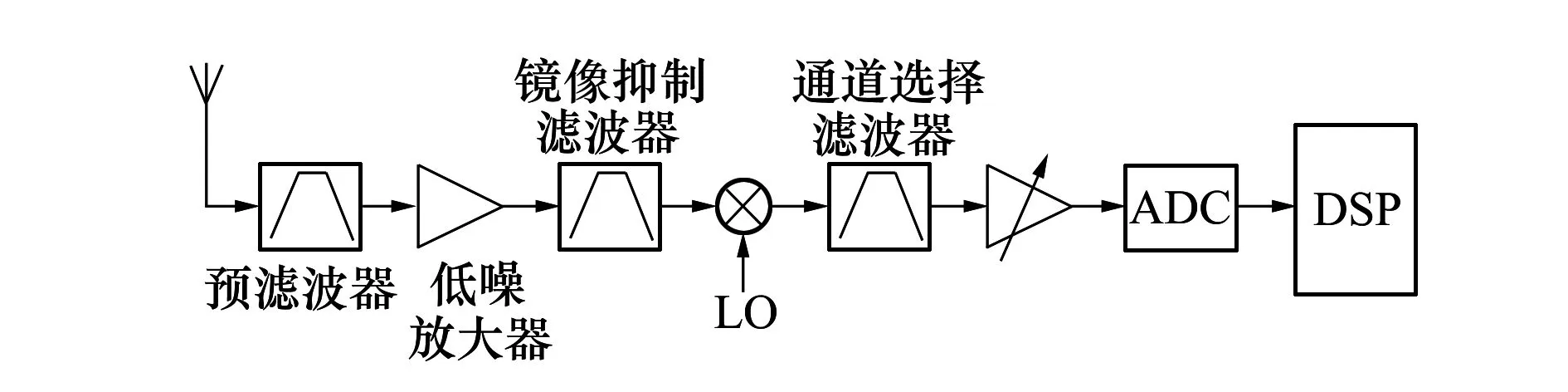
图1 外差式接收机结构框图

外差式接收机结构具有较好的性能,但是由于存在镜像干扰,镜像抑制滤波器(射频滤波器)和通道选择滤波器(中频滤波器)比较难做,成本较高。图1所示的接收机结构下,中频输出实信号,中频频率的选择首先要考虑到信号带宽B,至少应该大于B/2,否则会造成正负频率分量的混叠。

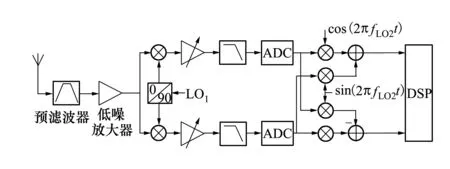
图2 低中频接收机结构框图

图2所示的低中频结构对射频信号进行复数变频,然后在I、Q路分别采样,输出频率较低的复数中频信号。之后在FPGA接收通道中进行数字复数下变频,并配合DSP完成捕获跟踪。这种结构既避免了外差式的镜像干扰,又缓解了零中频结构本振泄露、直流漂移等缺点[1]。低中频的中频频率可以低至信号带宽的1～2倍。

1.2 带通采样

为了降低接收机功耗以及A/D的实现验度，可以对中频信号进行带通采样。

采样过程在时域上可表达为信号与单位抽样函数序列的乘积,如(1)式所示。

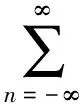
(1)

式中：Ts是单位抽样序列的周期,即采样周期。

单位抽样函数序列在频域中是间距fs(fs=1/Ts,采样频率)的冲激函数序列,任意函数与冲激函数的卷积有如下性质:

f(t-t1)*δ(t-t2)=f(t-t1-t2)

(2)

根据傅里叶变换的性质可知,原信号的时域采样相当于在频域与冲激序列卷积,即将原信号频谱以fs为单位进行搬移复制,如(3)式所示：

,m=0,±1,…,±∞

(3)

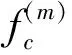
如上一小节所述,不同的射频前端结构会得到不同形式的中频信号,如传统外差式的实信号(具有双边对称频谱,称双边带信号),以及低中频结构的复信号(仅有单个频谱,称单边带信号)。2类信号的带通采样过程需要分别对待,下面进行详细说明。

1.2.1 双边带信号

对于仅具有一个频带的实信号(单频信号),带通采样后可能导致原频带与复制频带间的混叠,以及正负频率分量间的混叠。

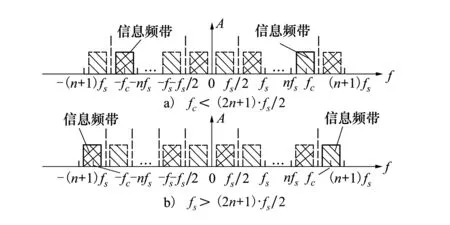
图3 双边带单频信号带通采样示意图

图3中,虚影为原信息频带采样后的复制频带。可以看到为了避免出现频率混叠,原信号的正(负)频谱分量必须位于频率范围[x(fs/2),(x+1)(fs/2)](x为整数)内。以图3a)为例,采样频率fs必须满足以下条件:

(4)

即

(5)

式中：n为非负整数,fc为信息频带正分量的中心频率(中频频率),B为信号带宽。考虑到信号带宽和滤波器通带的边界过渡性,采样频率一般选取为(5)式左右两端的中间值,即:

(6)

对于具有双/多个频带的实信号(双/多频信号),带通采样后可能引入的混叠除了单频信号的2种情况外,还可能存在来自多个频带之间的混叠。双频信号带通采样后的各频带在[x(fs/2),(x+1)(fs/2)]区间内有8种排列方式,详细内容可参考文献[4]。

1.2.2 单边带信号

如图4a)所示,对于单频复数信号,不会有正负频带分量间的混叠,只存在自身单个频带的混叠。因此,采样频率fs需满足:

(7)

即

(8)

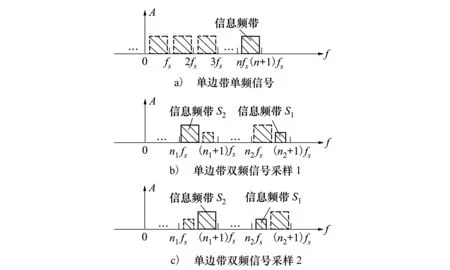
图4 单边带信号带通采样示意图

对于图4b)所示的双频单边带信号采样率必须满足以下条件:

(9)

即

(10)

式中：n1、n2为非负整数,fL1、fH1分别为信号频带S1的上下边沿频率,fH1、fH2分别为信号频带S2的上下边沿频率。

由(8)式和(10)式也可以得到类似于(6)式的等式。图4c)采样率的推导过程与图4b)类似。另外,多频信号的推导可参考文献[5]。

2 采样率与码速率

本文以GPS 6号卫星的C/A码为例研究采样率对接收机性能的影响。采样后的接收伪码与本地伪码的归一化相关函数为:

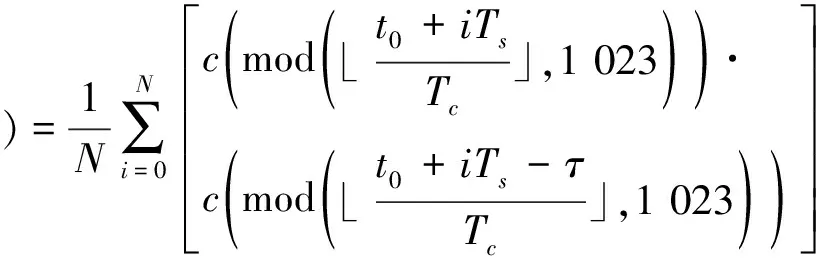
(11)

式中：Ts为采样周期,Tc为伪码码片周期,t0为采样点初相位(即首个采样点相对于接收伪码起始位置的距离),τ为本地伪码相对于接收伪码的延迟,c(n)为C/A码的第(n+1)个码片值(n=0～1 022),⎣·」为下取整函数,mod(a,b)表示a对b取余,N为预检测积分时间内的总采样点数。

设采样周期与伪码码片周期的关系为:

Ts/Tc=p/q

(12)

式中：p和q均为正整数,且p/q不可约。经过q个采样点后,采样点相对于伪码码片的位置将重复出现[6-7]。

若接收伪码和本地伪码在同一时刻的采样值都相同,则相关结果必为最大值。又因为采样点与码片的相对位置的重复周期为q,则满足相关结果最大的条件只需为:

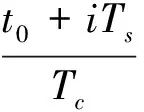
i=j,j+1,…,j+q-1

(13)

式中：j为非负整数。

图5为2种采样率下接收伪码及本地伪码时域采样的示意图,本地伪码的延迟处于使得相关结果从最大值开始变小的临界条件下。其中小三角形表示采样点,红点为码片边界标识,图5a)中Ts=Tc/3,t0=Tc/6,τ=Tc/6;图5b)中Ts=2Tc/3,t0=Tc/6,τ=Tc/6。对于图5a),将q=3,j=0,Ts=Tc/3,t0=Tc/6,τ=Tc/6代入(13)式中得:

(14)

解得:

-Tc/6<τ≤Tc/6

(15)

即当延迟τ满足(15)式时,相关结果为最大。可以发现,采样后的接收伪码与本地伪码的相关函数的最大值不是一个点,而是宽度为Tc/3的一个范围。对于图5b),按照上述做法可以得到与(15)式相同的结论。

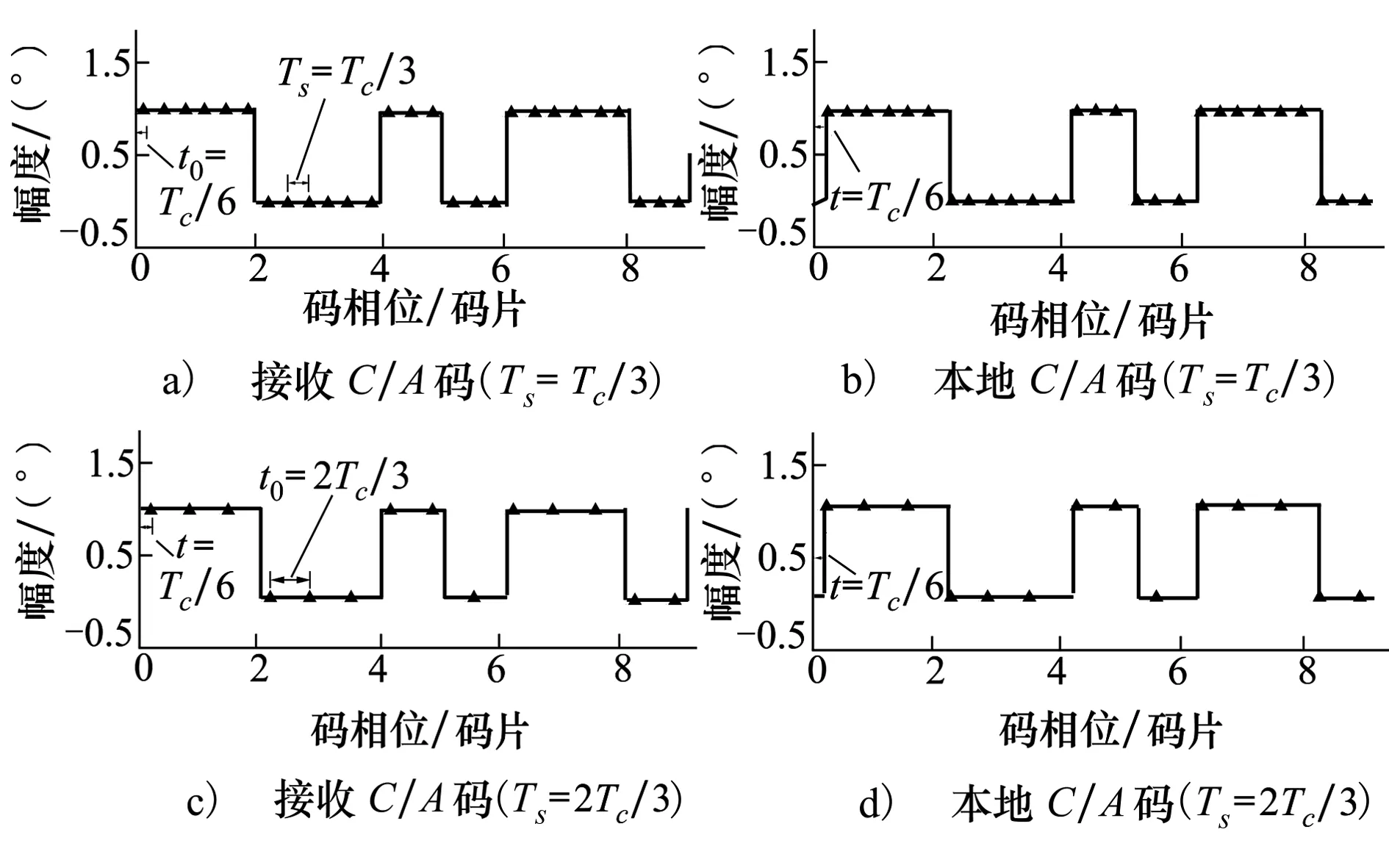
图5 不同采样率下接收伪码及本地伪码时域采样示意图

为了进一步研究和验证采样率与伪码速率的相对关系对相关结果的影响,本文做了图6所示的4个实验。图6a)、图6b)中各自选取了3种不同的采样初相位,采样周期Ts分别为Tc/3和2Tc/3;图6c)、图6d)中采样周期Ts分别为4Tc/15和101Tc/300,做出采样后的接收伪码与本地伪码的相关函数曲线。由图可以得到以下结论:

1) 比较图5a)、图5b)每个图中的3条曲线可以看出,采样后得到的相关函数呈台阶状,且采样点初相位仅影响相关函数在横轴的位移,而不影响其形状;

(2) 比较图5a)、图5b)间的曲线可以看出,Tc/3和2Tc/3采样率下得到的相关函数的台阶宽度是相同的,均为Tc/3,且与(15)式的结论一致。说明不同采样率下相关函数的台阶宽度也可能相同。

(3) 图5a)～图5d)中采样周期Ts分别为Tc/3、4Tc/15和101Tc/300,三者的采样率相差并不大,但是台阶宽度相差很大,分别为Tc/3、Tc/15和Tc/300,即Tc/q。进一步证实了相关函数的时间分辨能力仅与q有关,q越大,时间分辨能力越强。

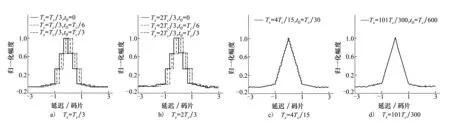
图6 不同采样率下接收伪码与本地伪码的相关函数

由(12)式得Ts=(p/q)Tc,当采样率近似相等时,p越小,q则越小,从而时间分辨能力越差。而正整数p最小为1,说明在同等采样率等级下,p取1(即采样率为伪码速率的整数倍)时相关函数的时间分辨能力最差。但并不是说只要采样率选择为伪码速率的非整数倍就能得到好的时间分辨能力。因此，文献[6-9]中提出的采样率选为伪码速率非整数倍仅是获得良好相关函数时间分辨能力的必要条件,而非充分条件。

3 采样率与相关器间距

图7所示为采样后的3路超前、即时、滞后本地伪码与接收伪码的相关函数及超前减滞后鉴相曲线[11-12]。图7a)的采样周期Ts为19Tc/5,3路本地伪码的码相位偏移(即相关器间隔)为3Tc/5,图7b)为图7a)的鉴相曲线。

文献[10]中给出一个例子,当相关器间隔为3Tc/5时,每个码片上的采样点个数至少为10,即Ts最大为Tc/10。而图7中相关器间隔d同样为3Tc/5,采样周期为19Tc/5(远大于Tc/10),仍可以得到很好的鉴相曲线。很明显,文献[10]的结论是不正确的。并且根据上一节得出的结论可知,相关函数的时间分辨能力为仅与q有关,q越大,相关函数的台阶越窄,时间分辨能力越强。在图7所示的相关器间隔下,只要q越大,超前和滞后支路的相关曲线在时域上就越能够分离开,鉴相曲线线性区间的线性度也就越好,与采样率和伪码速率的倍数之间没有必然联系。

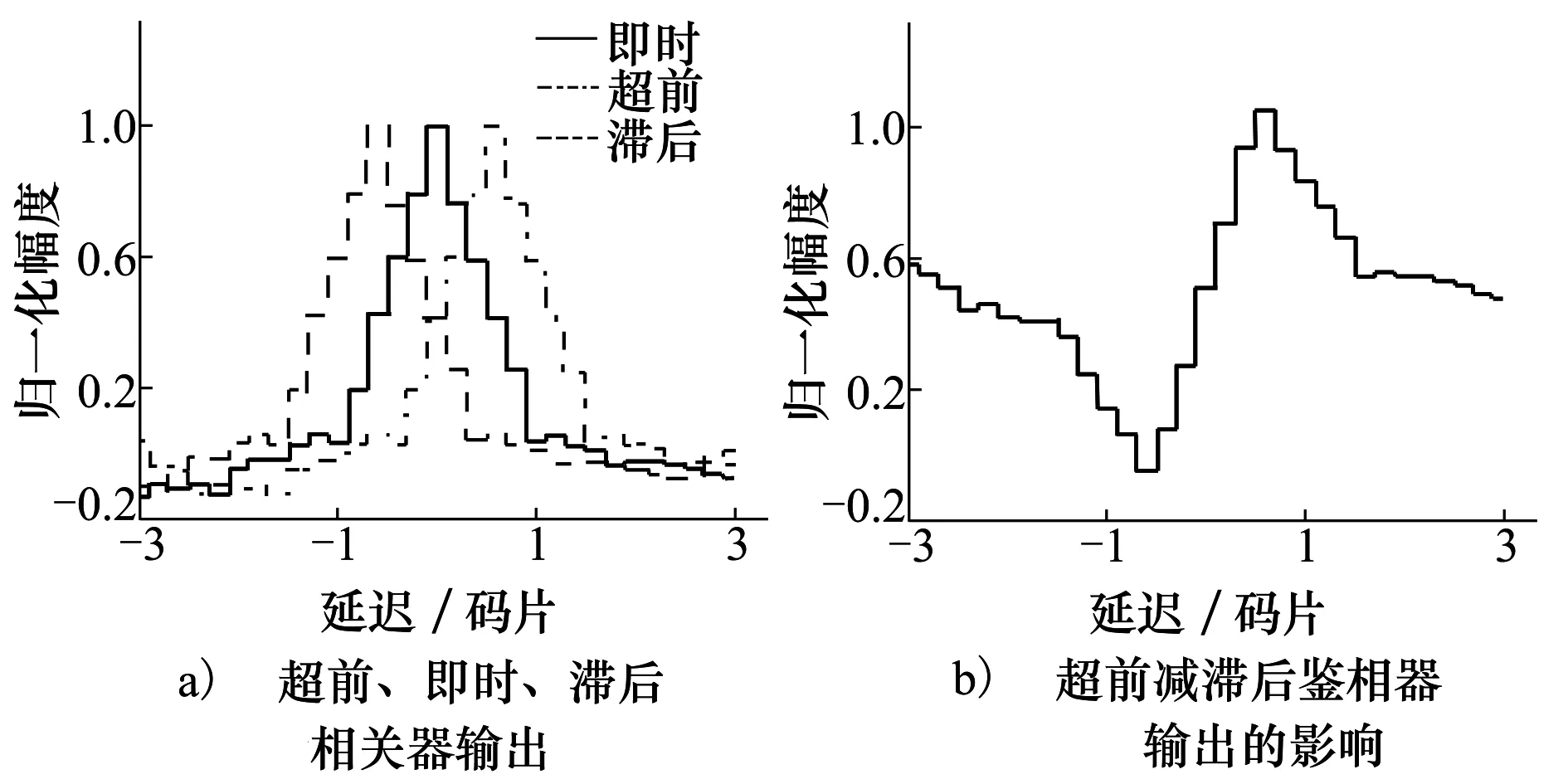
图7 采样率对相关器及鉴相器输出的影响

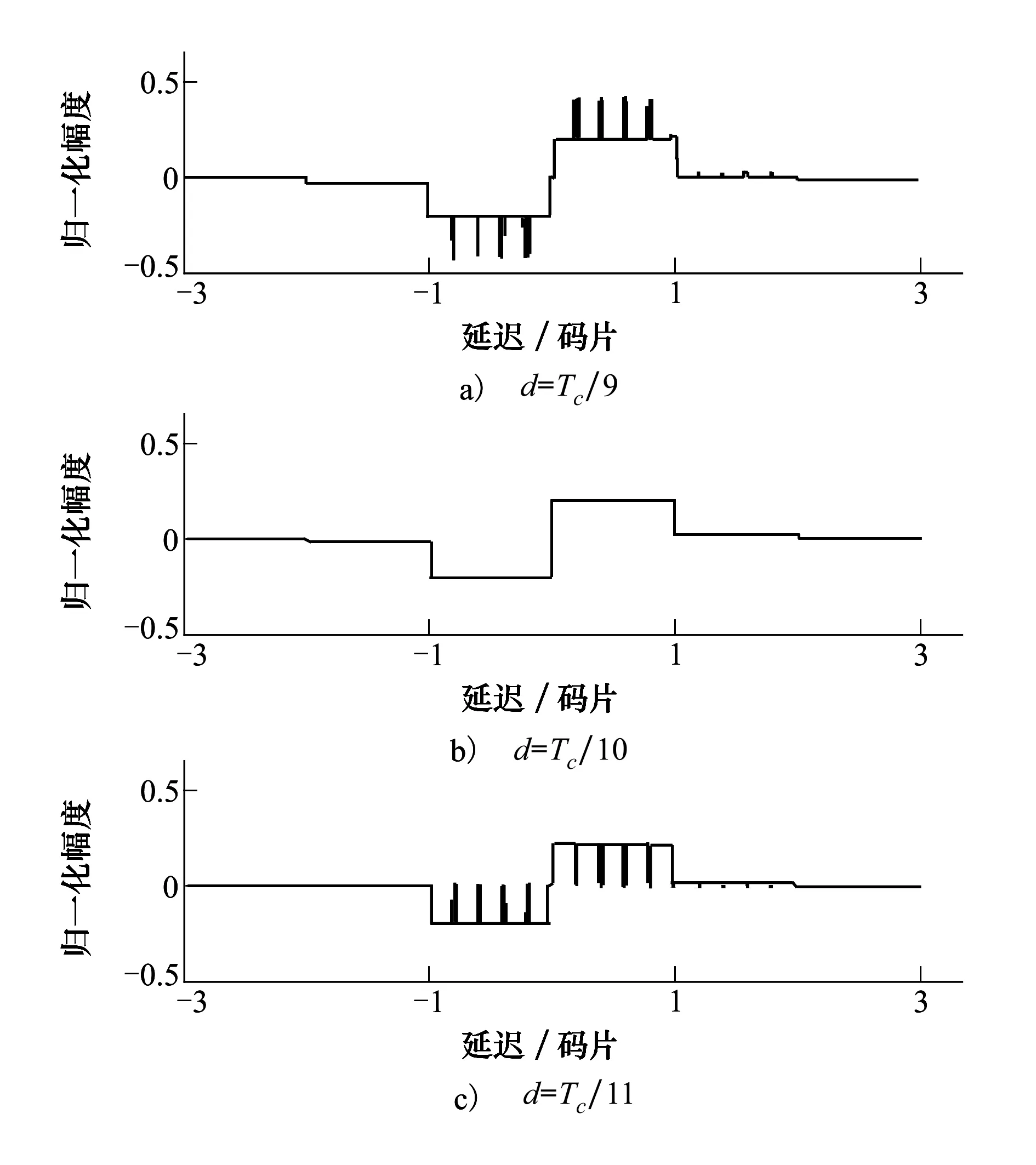
图8 采样率的选择与相关器间隔的关系

为了进一步研究相关器间隔对采样率设计的影响,本文做了图8所示的3个仿真实验。图8的采样周期Ts均为(n/5)Tc,其中n为正整数,且n/5不可约;相邻相关器间隔分别为Tc/9、Tc/10和Tc/11。

由图8b)可以看出,当相关器间隔为Tc/(2q)时,鉴相曲线没有过零点,不存在线性区间,跟踪环路无法工作;图8a)中相关器间隔稍大于Tc/(2q),出现线性区间,环路可以工作;图8c)中相关器间隔稍小于Tc/(2q),出现了多个零点,不利于跟踪。由此得出结论,当相关器间隔满足d>Tc/(2q)时,即

q>Tc/(2d)

(16)

跟踪环可以工作。

4 结 论

综合以上的研究和讨论,可以得出以下几条采样率设计策略:

1) 为了降低信号处理的速度,以降低成本和功耗,要求采样率尽量低。

2) 对于射频前端输出的中频信号,要在频谱不混叠的前提下完成带通采样。实数中频信号采样率的设计可参考(5)式、(6)式;复数中频信号采样率的设计可参考(8)式、(10)式。

3) 设采样率与伪码速率满足(12)式的条件,采样后的接收伪码与本地伪码的自相关函数的时间分辨能力仅与q有关。q越大,相关函数的台阶越窄,时间分辨能力越强。

4) 相关器间隔为d,当q满足(16)式时,超前减滞后鉴相曲线存在线性区间,环路可以工作。且q越大,线性区间的范围越大,线性度越好。

参考文献：

[1] Mirabbasi S, Martin K. Classical and Modern Receiver Architectures[J]. IEEE Communications Magazine, 2000, 38(11): 132-139

[2] Dennis M Akos. A Software Radio Approch to Global Navigation Satellite System Receiver Design[D]. USA: Ohio University, 1997

[3] Akos Dennis M, Ene Alexandru, Thor Jonas. A Prototyping Platform for Multi-Frequency GNSS Receivers[C]∥Proceedings of the ION GPS/GNSS, 2003: 117-128

[4] Tseng Chinghsiang, Chou Sunchung. Direct Downconversion of Multiple RF Signals Using Bandpass Sampling[C]∥IEEE International Conference on Communications, 2003: 2003-2007

[5] Liu Jiecherng. Bandpass Sampling of Multiple Single Sideband RF Signals[C]∥Communications, Control and Signal Processing, 2008: 863-866

[6] Quirk K J, Srinivasan M. Analysis of Sampling and Quantization Effects on the Performance of PN Code Tracking Loops[C]∥IEEE International Conference on Communications, 2002: 1480-1484

[7] Quirk K J, Srinivasan M. PN Code Tracking Using Noncommensurate Sampling[C]∥IEEE Trans on Communications, 2006: 1845-1856

[8] James Bao-Yen Tsui. Fundamentals of Global Positioning System Receivers-A Software Approach[M]. 2nd Ed. USA: Wiley-Interscience, 2004

[9] 柯颋,胡修林,刘禹圻,等. GNSS接收机中采样率对时间鉴别力的影响[J]. 宇航学报,2010, 31(12): 2722-2729

Ke Ting, Hu Xiulin, Liu Yuqi, et al. Influence of Sampling Rate on Time Discrimination in GNSS Receiver[J]. Journal of Astronautics, 2010, 31(12): 2722-2729 (in Chinese)

[10] Liu Liyu, Amin Moeness G. Performance Analysis of GPS Receivers in Non-Gaussian Noise Incorporating Precorrelation Filter and Sampling Rate[C]∥IEEE Trans on Signal Processing, 2008: 990-1004

[11] 谢刚. GPS原理与接收机设计[M]. 北京:电子工业出版社,2009

Xie Gang. Principles of GPS and Receiver Design[M]. Beijing: Electronics Industry Press, 2009 (in Chinese)

[12] Kaplan Elliott D, Hegarty Christopher J. Hegarty. Understanding GPS Principles and Applications[M]. 2nd Ed. USA: Artech House, 2005