基于车头间距与前车速度的改进优化速度模型

赖林, 胡永红, 史忠科

(西北工业大学 自动化学院, 陕西 西安 710072)

在交叉路口中,为更好地实现对交通流的良好调控,须控制好信号灯。排队长度、交通流模型等可为信号灯的周期设置提供理论依据[1]。

1995年,Bando等人[2]首次提出优化速度模型,弥补了之前Newell模型中不能模拟诸如车辆在红灯转绿灯时加速等情形的缺陷,但该模型会产生过高的加速度以及不符合实际的减速度,甚至造成撞车的局面,因此在此模型的基础上,Helbing和Tilch等人[3]提出了广义力模型。Treiber等人[4]研究发现,当碰到前车的速度远大于跟驰车的速度时,即使车头间距要比安全距离小,跟驰车也不会因此而采取减速措施,这一情况在优化速度模型和广义力模型中都不适用。针对于这一问题,姜锐等[5]提出了全速度差模型,从而很好地解释了这一现象。Zhao和Gao等人[6]通过仿真后发现,如果跟随车速度与前车速度较为接近时,它们之间的速度差便为零或者为较小值,如果碰到突发事件,前车会突然制动而以较大加速度减速行驶,这种情况广义力模型和全速度差模型都无法得到很好解释,前后两车会发生碰撞。因此,基于此情况,他们通过加入加速度差值,进一步改进了全速度差模型,从而得到一个新的跟驰模型。这一模型能够有效地应对类似的紧急情况,从而避免出现撞车等事故。基于以上几个模型,更多的影响因子被考虑到模型之中,从而一系列的新模型相继由各学者提出[7-8]。一些学者通过将更多前车的车头距等信息考虑进来,从而提出扩展的优化速度模型,比如Ge和Zhu等人[9]通过添加跟随车车头距因素的影响,从而扩展了优化速度模型。从优化速度模型的发展看,对它的研究多停留在理论和仿真阶段,并未使用足够的实测数据来对模型进行验证,同时也没有考虑到交叉路口等道路情况的特殊性。本文通过采集大量的实测数据对优化速度模型进行验证,发现该模型存在响应频率不够、加速度过大、与实测数据的偏差较大和随着时间推移而逐渐发散等问题。针对仿真验证过程中出现的问题,在优化速度模型的基础上,简化了时变期望间距的表达式,添加了两车车头间距和前车速度对于加速度的影响,得到能够更加准确描述实际跟驰行为的改进优化速度模型。

1 优化速度模型分析

对于优化速度(OV)模型,其表达式为

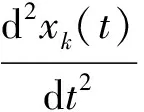
(1)

式中：α为驾驶员反应敏感系数,xk(t)为t时刻后车的位置,V(Δxk(t))为优化速度。

对于优化速度函数V(Δxk(t)),其表达式为

(2)

式中：vmax为行车速度最大值,Δxk(t)为t时刻两车车头间距,hc为行车安全距离,为固定值。

为了验证OV模型是否适用于交叉路口中车辆间的跟驰行为,需要获取若干组实测数据。选择西安市边家村交叉路口作为数据采集地点,通过三脚架把DV固定在天桥上,对南北走向的道路进行纵向拍摄,获得一段时间内的视频资料,视频帧率为25帧/s。选取其中某些处于跟驰状态的车辆作为研究对象,对视频段进行逐帧截图,获得连续变化图像。测得实际道路中车道线白线段纵向长度2 m,纵向间距3.8 m,建立图像坐标系,选取某些特定位置坐标,通过matlab等数学工具进行直接线性变换,得到图中位置与实际位置的转换关系。根据测量车道线实际长度等数据进行验证,由此换算得到的车辆实际位置值较为准确。最后选取前后两车某个特定位置作为参考点,统计每一帧图像中车辆的像素点坐标,换算成实际位置,绘制车辆的位置变化曲线,该拟合曲线对应的导数曲线为车辆的速度变化曲线。

在获取数据之后,选取某一时刻为初始点,两车位置及速度已知,设置仿真步长为T,通过以下离散迭代公式对优化速度模型进行验证,式中加速度ak(t)通过OV模型表达式计算得到:

(3)

(4)

根据观测,该路段的最大速度取值为10 m/s,代入实测数据进行仿真,得到车辆的速度与间距变化曲线,如图1所示。

图1 第一组实测数据及仿真结果

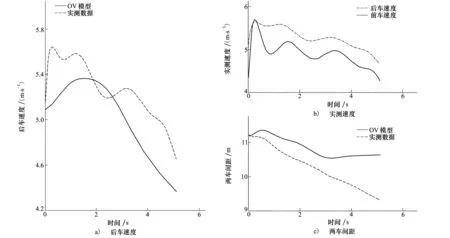
图2 第二组实测数据及仿真结果

由上述多组仿真结果可以看出,OV模型并不能准确地反映实际的车辆跟驰行为,往往存在响应频率不够、加速度过大以及与实测数据的误差较大等问题,并且随着时间推移,处于发散状态。由优化速度公式可知,对于优化速度,影响因子为时变车头间距与大小恒定的期望间距,容易导致优化速度变化过快,从而造成后车的加速度过大,变化过快,同时,后车加速度需要时刻受到前后车的速度与间距的调控,使后车保持稳定的行驶状态。

2 模型改进

通过对OV模型的仿真验证发现,期望间距hc取固定值时结果并不理想,论文结合文献[10]提出的时变期望间距hc(t)表达式做进一步改进。

hc(t)=

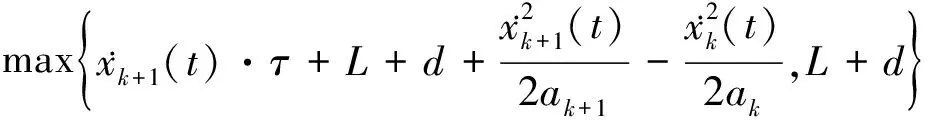
(5)

假设τ为变化值,τ与后车速度存在这样一种关系,当后车速度较大时,τ取值较小,而后车速度较小时,τ取值较大,因此,对τ的表达式重新进行构造,如下:

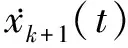
(6)

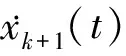
代入τ到hc(t)表达式后化简,约去反应时间τ,得到如下公式:

(7)

式中：La为大于最小车头间距的一个常数项,取值与车辆行驶状态有关。

综合得到时变期望间距hc(t)的表达式:

(8)

原有时变期望间距存在着数值偏大、变化偏快等问题,从而导致优化速度与后车加速度与实际值存在一定的偏差,而改进后的期望间距削弱了后车速度与司机反应时间的影响,变化幅度减小,与实际情况更为接近。

通过对OV模型的仿真可以看出,前车速度大于后车时,仿真加速度数值容易过大,受前车速度的影响较大,前车速度小于后车时,仿真加速度会受到两车间距的影响,往往大于实际值。因此,根据前后两车速度关系,添加一个跟前车速度与两车间距有关的加速度补偿项,实现对后车的加速度在合理范围内进行调整,使加速度更加接近实际值,构造如下加速度补偿公式:

(9)

式中：m1与m2为常数项,与实际驾驶情况有关。

综合以上分析,得到改进OV模型表达式,如下:

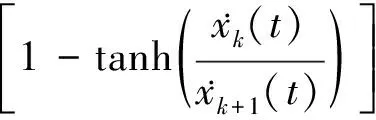
hc(t))+tanh(hc(t))]

(10)

3 实验结果对比分析

根据多组实测数据,对该改进模型进行仿真验证,分别得到经典OV模型与改进模型的后车速度及两车间距的仿真结果,同时进行对比分析,两车间距以及后车速度的仿真结果如图3所示。

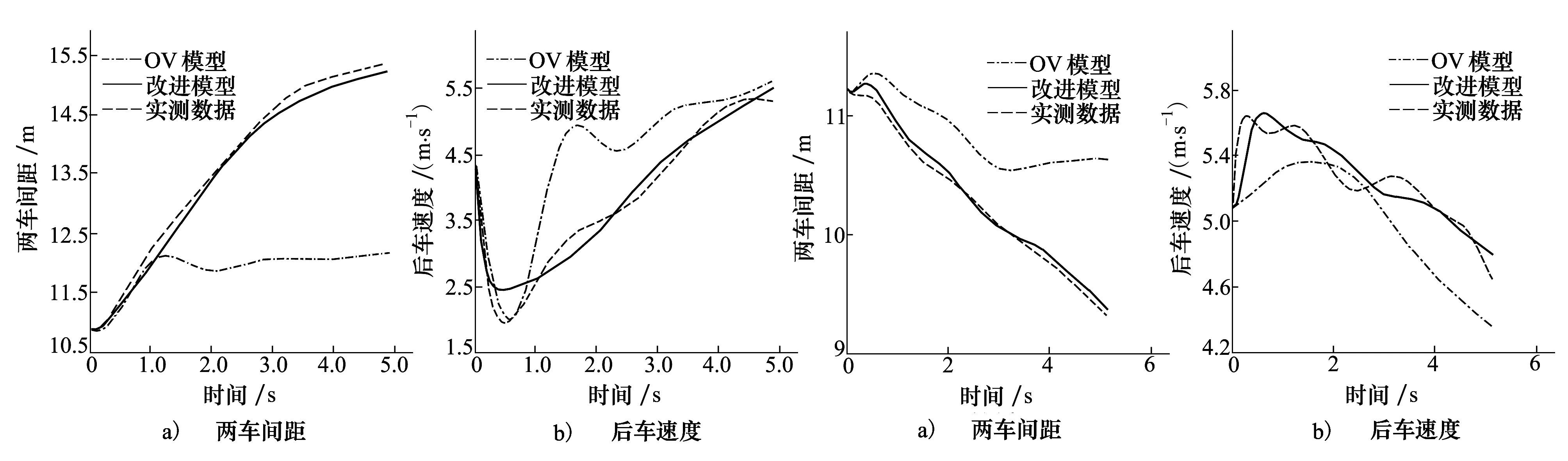
图3 第一组数据仿真结果 图4 第二组数据仿真结果

改进后的模型简化了时变期望间距表达式,在考虑前后车速度关系的基础上,添加了前后车速度以及间距对后车加速度的影响,对后车加速度调整后,提高了响应速率,减小了后车加速度的波动范围,使模型的变化趋势与实际更加接近。通过对比多组实验结果以及比较分析误差情况可以看出,改进模型的仿真结果与实测数据更加接近,误差更小。

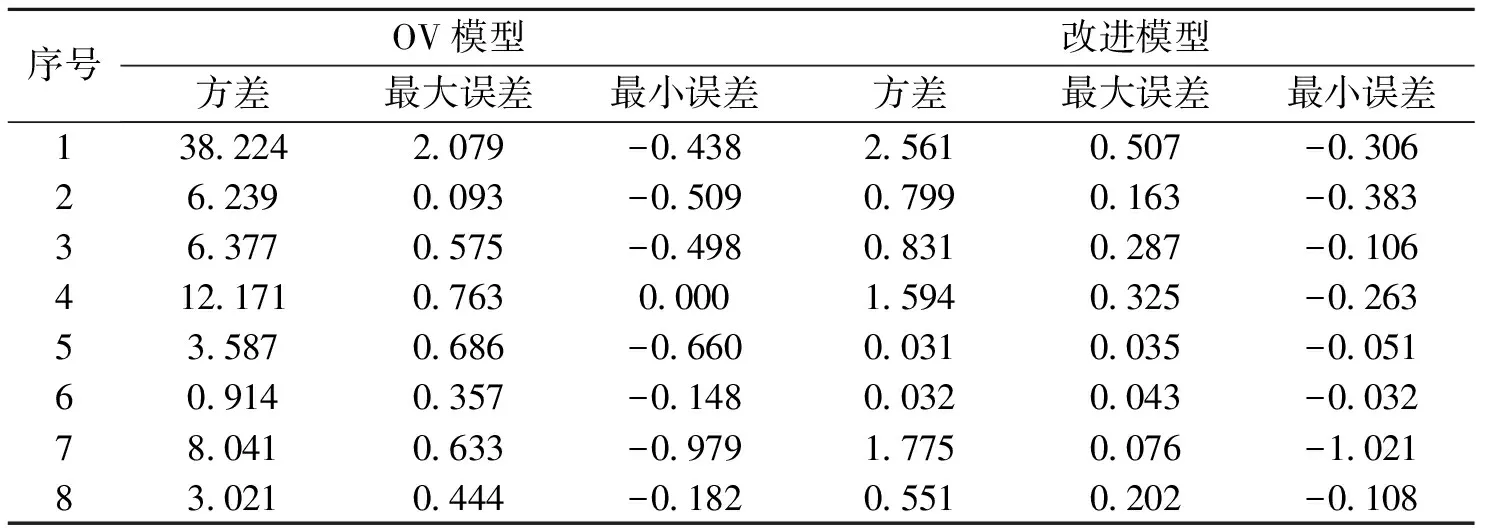
表1 误差分析

4 结 论

原有的优化速度模型不能准确描述交叉路口中车辆间的跟驰行为,针对这一问题,本文从两车车头间距及前车速度会对后车加速度产生影响的观点出发,简化了时变期望间距表达式,根据前后车速度之间的大小关系,添加了与车头间距与前车速度有关的加速度补偿项。结合多组实际数据对改进模型进行验证,对比原有优化速度模型,结果表明,改进后的模型与交叉路口车辆间的实际跟驰行为更为接近。

参考文献：

[1] 史忠科, 黄辉先, 曲仕茹,等. 交通控制系统导论[M]. 北京: 科学出版社, 2003

Shi Z K, Huang H X, Qu S R, et al. Introduction of Traffic Control System[M]. Beijing: Science Press, 2003 (in Chinese)

[2] Bando M, Hasebe K, Nakayama A, et al. Dynamical Model of Traffic Congestion and Numerical Simulation[J]. Phys Rev E, 1995, 51(2): 1035-1042

[3] Helbing D, Tilch B. Generalized Forcemodel of Traffic Dynamics[J]. Physical Review E, 1998, 58(1): 133-138

[4] Treiber M, Hennecke A, Helbing D. Derivation, Properties, and Simulation of a Ges-Kinetic-Based, Nonlocal Traffic Model[J]. Physical Review E, 1999, 59(1): 239

[5] Jiang R, Wu Q, Zhu Z. Full Velocity Difference Model for a Car-Following Theory[J]. Physical Review E, 2001, 64(1): 017101

[6] Zhao X, Gao Z. A New Car-Following Model: Full Velocity and Acceleration Difference Mode[J]. The European Physical Journal B-Condensed Matter and Complex System, 2005, 47(1): 145-150

[7] Tang T Q, Li C Y, Huang H J. A New Car-Following Model with the Consideration of the Driver′s Forecast Effect[J]. Physics Letters A, 2010, 374(38): 3951-3956

[8] Helbing D. Derivation of Non-Local Macroscopic Traffic Equations and Consistent Traffic Pressures from Microscopic Car-Following Models.∥Modelling and Optimisation of Flows on Networks[M]. Springer Berlin Heidelberg, 2013: 247-269

[9] Ge H X, Zhu H B, Dai S Q. Effect of Looking Backward on Traffic Flow in a Cooperative Driving Car Following Model[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2006, 54(4): 503-507

[10] 李迎峰，史忠科，周致纳，等. 基于时变期望车距与最大车速的跟驰模型[J]. 交通与计算机，2008，26(3)：1-4

Li Y F, Shi Z K, Zhou Z N, et al. Car-Following Model Based on Time-Variable Expectation-Headway and Maximal Velocity[J]. Computer and Communications, 2008, 26(3): 1-4 (in Chinese)