一种基于转矩可达集的操纵面组合分配设计方法

史静平, 屈晓波, 毕可军

(1.西北工业大学 自动化学院, 陕西 西安 710072; 2.飞行器一体化技术重点实验室, 陕西 西安 710072)

先进飞机操纵面的分配设计[1-2]的含义有2个层面:①确定舵面在不同飞行任务下的组合方案;②在此基础上确定匹配的舵面分配算法。目前的研究成果多集中于具体分配算法的研究上,如:早期的伪逆法[3]、加权伪逆法[4],在此基础上改进的级联广义逆法[5]、再分配伪逆法[6],以及20世纪90年代中期提出的直接分配法[7]、面搜索法[8]、对边搜索法[9]、基于数学规划的分配法[10]等。在具体分配算法的研究上取得的理论成果可谓颇丰,但在操纵面组合分配的研究上,成果有限,现有的方法多采用基于数学规划的分配方法,即:针对不同的飞行任务建立相应的舵面分配优化指标,采用线性规划、二次规划等数学方法进行寻优求解,如:基于二次规划的多目标分配方法[11]、基于基排序线性规划的分配方法[12]等,这些方法虽然在数学上较好地解决了操纵面组合与分配求解,但工程应用仍存在一些亟待解决的问题,例如:①数学规划类方法需要在线寻优,由于实时性问题难以直接应用;②数学规划类方法将所有的舵面放在一起分配,没有充分考虑舵面的实际物理特性,某些组合方式产生的分配解可能会导致相邻舵面间产生复杂的气动耦合效应,不利于实际控制;③数学规划类方法需要根据各飞行阶段进行模态切换,这极大地增加了控制系统设计的复杂度。

针对上述问题,本文提出了一种基于转矩可达集(AMS: Attainable Moment Subset)设计的操纵面组合分配方法,该方法首先计算出各个基控制组的转矩可达集,在此基础上综合分析各个基控制组转矩可达集构造特点,结合雷达反射特性和阻力特性确立一组主控舵面,以使现有常规布局飞机的控制律设计方法和经验得以沿用。当主控舵面不能满足机动飞行对于可用力矩的需求时,启用其他辅助操纵面及推力矢量操纵面,辅助操纵面的管理按照舵面偏转对于雷达反射的优先级进行。随后的仿真验证了该方法的有效性。

1 问题的描述

设飞机期望的力矩向量是v(t)∈R3,操纵面的偏转量为u(t)∈Rm,控制分配就是在给定v(t),及控制效率矩阵B:Rm→R3(m>3)的情况下,求解不定方程:

Bu(t)=v(t)

(1)

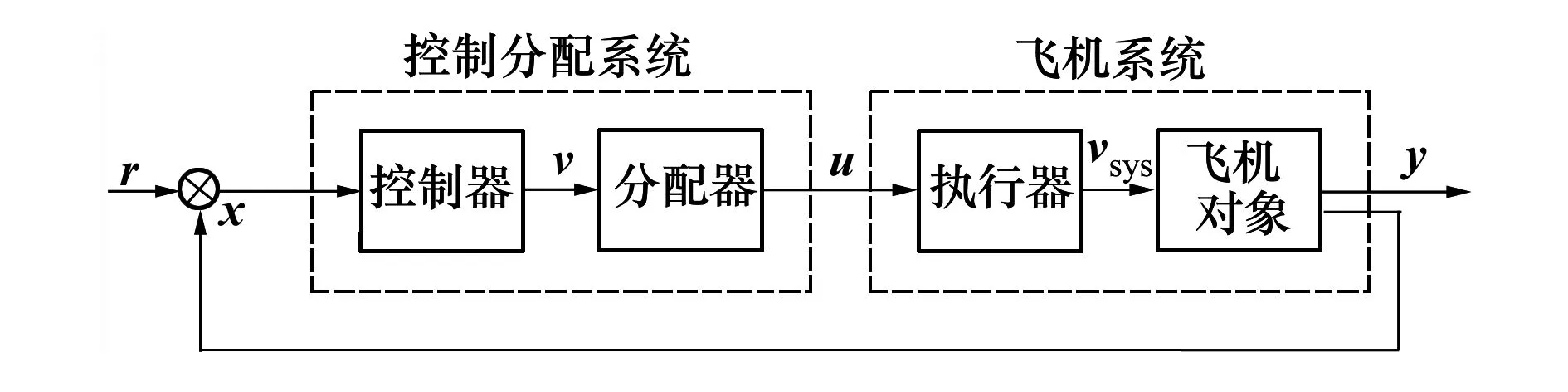
图1 多操纵面控制系统结构图

操纵面的控制分配应与飞机的飞行任务相结合,一般来说,飞机的飞行由起飞/爬升、巡航、突防、大机动飞行、下降/着陆等几个阶段构成。在操纵面组合方案设计时,应根据不同的飞行任务建立起相应的操纵面分配指标。现有的基于数学规划的方法在解决该问题时,所采用的研究思路可概括为如下2个优化过程:

,u∈Θ

Θ=argmin‖W(Bu-v)‖p,u∈Ω

这种方法在分配时将所有可用的控制面同时调动起来,根据各阶段的优化指标输出操纵面偏转量。这种方法在解决多目标分配问题的同时,也带来了新的问题,即:如何根据飞机各阶段的飞行特点辨识出当下的分配指标。是通过飞行员手动切换,还是通过态势感知的原理智能地决策出分配指标,抑或是简单地将多目标分配问题转化为单目标分配问题取得一个次优解。客观地讲,不论是采用哪种方式,对控制系统设计都带来了极大的挑战,即便是人工手动切换也增加了操控系统设计的复杂度。从工程角度看,同时调用所有控制面参与分配不利于系统的可靠性,各模态自动切换带来的难度也增加了控制系统设计的负担。此外,不同舵机的速率并不相同,不加以区别同时调用也不合理,特别是对于推力矢量等异构操纵面更应区别对待。

本质上,不论是何种舵面组合方式,都应该首先满足飞机运动对于力矩的需求,在此基础上使分配解满足各阶段的分配指标。基于这种考虑,本文提出了一种基于转矩可达集设计的操纵面组合分配方案:首先将操纵面分成若干可行的基控制组,并计算各个基控制组的转矩可达集;然后结合工程经验选择具有较大转矩可达集的基控制组作为主控制组,其他舵面作为辅助操纵面,并根据雷达反射特性对辅助操纵面进行优先级排序;在实际飞行时,若主控制组不能满足飞机对于可用力矩的需求,根据优先级启用辅助操纵面。

本文的行文流程如下:首先对转矩可达集的求解方法进行研究,然后给出基于转矩可达集设计的操纵面组合分配方法。

2 转矩可达集的求解

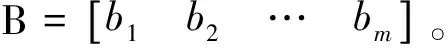
(2)

式中:k≠a,b,c,i,j,分析(2)式的结构可得到如下结论:

1) 当ui、uj、uk为常值,ua、ub、uc在定义域内自由变化时,映射后所形成凸体Φ3为一盒体。

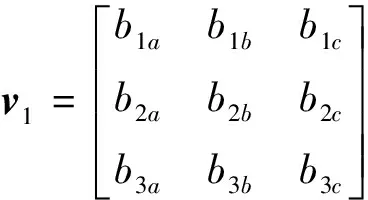
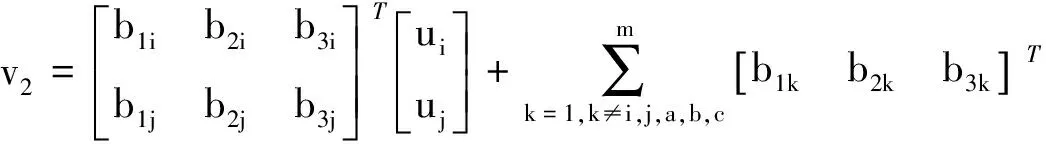
通过上面讨论可知:若B的任意3×3子矩阵满秩,只要允许3个控制变量自由变化,则其形成的集合v1必为凸体。因此在B的任意3×3子矩阵满秩的情况下,Φ3的平面P只可能是控制向量u的N(N<3)个元素自由变化,其他(m-N)个元素处于常值状态,具体的:

当N=1,即1个变量自由变化时,rank(v)=1,因此映射v=Bu形成的集合为直线段;

当N=2,即2个变量自由变化时,rank(v)=2,因此映射v=Bu形成的集合为有限的平面。

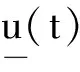
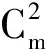
图2 Φ3的几何构造(m=4)

设集合ξi,j是u中的元素ui和uj在定义域内自由变化,其它元素处于常值时所确定的一组平行平面:

(3)

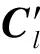
B′(1,i)=0

B′(1,j)=0

(4)

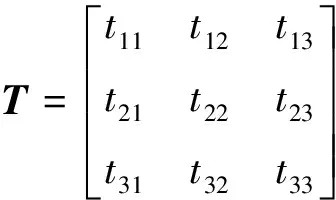
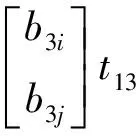
(5)

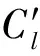
(6)

式中:η为平面ξi,j的法向量:η=bi×bj。设∂(Φ3)的2个外表面为fi,j。当控制量uk取值使Clk极大或极小时所对应的平面ξi,j即为Φ3的表面fi,j,因此根据ηT·bk符号与Clk的取值关系便可以确定(m-2)个控制量的取值。例如:正向表面fi,j的4个顶点为:

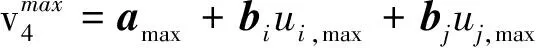
(7)

式中:

μk,max

(8)

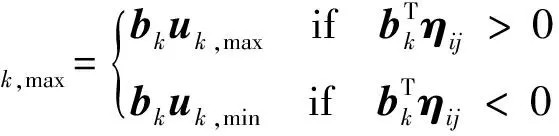
(9)

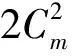
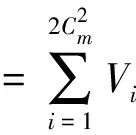
(10)

通过求解Cl、Cm、Cn轴与边界∂(Φ3)的交点,可以获取飞机在三轴力矩上的跨度。

当控制效率矩阵不满足任意3×3子矩阵满秩时,会出现ηT·bk=0的情况。对于此种情况,可通过“小扰动破坏其相关性”使问题得以求解。

3 基于转矩可达集的操纵面组合分配设计

战斗机的飞行一般由起飞/爬升、巡航、突防、大机动飞行、下降/着陆等几个阶段构成。为了提高飞机的性能,在控制系统设计时通常期望操纵面的控制与分配能够满足:在超声速巡航阶段,操纵面偏转产生的阻力最小,以减小燃油;在突防阶段,操纵面偏转产生的雷达反射最小,以减小威胁;在大机动阶段,飞机可用力矩最大,以增加飞机敏捷性。如前文所述,如果对于各飞行阶段均建立相应的分配模态进行操纵面分配设计,将大大增加控制系统设计的复杂度,并不利于工程实际的应用。

事实上,目前欧美先进战斗机的主控舵面与辅助操纵面的区别依然是较为明显的。例如:美国第四代战斗机F-22虽然拥有12个可控舵面,但通常情况下仍然仅利用升降舵、方向舵和副翼3个主操纵面控制飞机运动,其他舵面仅在主控舵面气动效能不足时使用,如:过失速机动、主控舵面损伤时,而对于舵面雷达反射特性和超巡阻力特性的考虑,主要是在翼型设计、气动布局设计时完成的;俄罗斯的三翼面布局飞机Su-30MKI和Su-33,它的主控舵面也由升降舵、副翼和方向舵构成,鸭翼(小翼)主要起到增升和增大可用迎角的作用。就目前飞行器发展的现状而言,操纵面的控制分配设计不能忽略舵面间的区别而简单地进行纯粹数学意义上的组合与分配。在对多操纵面布局飞机的控制系统进行设计时,仍应首先确定一组主控舵面,以使现有常规布局飞机的控制律设计方法和经验仍然得以沿用。当主控操纵面不能满足飞机机动飞行对于力矩的需求时,启用辅助操纵面或推力矢量操纵面;对于辅助操纵面的调度与管理可按照舵面对于雷达的反射特性和阻力特性进行。

根据上述思想,本文给出了一种基于转矩可达集的操纵面分配设计方法。由于多操纵面控制分配有2个主要的任务：①合理的组合多种控制面,使飞机能够适应不同的飞行任务和飞行条件;②在控制面发生故障的情况下仍然能通过剩余控制面的重新组合[13]来协同控制飞机运动,从而提高飞机对故障及损伤的鲁棒性。因此,本文提出的方法也兼顾考虑了操纵面故障时的分配情况。为了描述该过程,首先引入基控制组和控制效率基的概念[12]。

定义对于某个分配系统,若其任意n(m≥n≥3)个操纵面ui=[u1,u2,…,un]的控制效率向量(b1,b2,…,bn)之间线性无关,则称该组操纵面ui为分配系统的一个基控制组,将其效率向量构成的组合Bbase=[b1,b2,…,bn]称为该基控制组的效率基。

根据该定义,对于任意3×3子矩阵满秩的分配系统,它的任意3个操纵面都可构成一个基控制组,每个基控制组均能够为飞机提供三轴力矩。多操纵面布局飞机的基控制组是不唯一的,我们可以通过计算基控制组的转矩可达集对基控制组的效能进行评价。基控制组的转矩可达集体积越大,则其可提供的力矩效能越高。

主操纵面应具备控制飞机完成大部分机动飞行的能力,因此主操纵面应具备较好的气动特性,其控制效率向量构成的效率基应具有较大的转矩可达集,这样也可以避免辅助操纵面、推力矢量操纵面频繁的调度,进而降低发动机的维护费用。本文提出的基于转矩可达集的操纵面组合分配方法具体设计步骤如下:

1) 首先将推力矢量操纵面之外的(m-3)个操纵面进行组合,选出线性无关的多个基控制组。

2) 分别计算各个基控制组对应的转矩可达集体积,并将其按大小排序。

3) 对排好序的各个基控制组进行比较,综合考察各组舵面的阻力、升力和雷达反射特性,结合工程经验选择具有较大转矩可达集的基控制组作为主控操纵面。其余的基控制组按转矩可达集体积大小进行优先级排序,作为备用控制组,当主控制组发生故障时使用。

4) 将主操纵面列表之外的操纵面作为辅助操纵面,当主操纵面控制组不能满足飞机大机动飞行对于力矩的需求时,启用辅助操纵面;当辅助操纵面也不能满足需求时,启用推力矢量操纵面。

5) 启用辅助操纵面时,飞机通常处于突防或大机动状态,因此对于辅助操纵面的调度与管理按照舵面对于雷达反射的优先级进行。

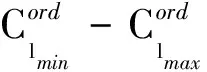
图3 操纵面分配结构示意图

通过对三轴可用力矩的监测,该方法实现了对于舵面调度的分配与管理,同时也兼顾考虑了舵面分配对于隐身能力的影响,并实现了舵面故障情况下的重构控制。

此外,飞机在起飞/着陆阶段要求具备较好的升力特性,这一阶段目前主要依赖飞行员手动操纵襟翼来提高飞机的升力。文献[13]中介绍了一种先进布局飞机的分配方案,其分配方案的切换与飞行任务的内容、迎角的大小等因素相关联。如何根据飞机的飞行状态和任务自动切换分配模式仍然有待进一步的深入研究。

4 仿真验证

某飞机在30 000 ft,0.3Ma,a=12.5°时的控制效率矩阵B为:

B阵的3行分别为各操纵面的滚转操纵效率值、俯仰操纵效率值、偏航操纵效率值。三轴力矩与操纵面偏转角的关系满足线性假设:

Bu=v

各操纵面的位置限制如表1所示。其中,操纵面u1、u2为右、左升降舵的偏转角,u3、u4为右、左副翼的偏转角,u5为方向舵的偏转角,u6、u7为右、左前缘襟翼,u8、u9、u10分别为矢量发动机在滚转、俯仰、偏航方向的偏转角。

表1 操纵面位置限制

为了对该飞机进行操纵面分配设计,首先确定其主控制组,将可能的基控制组列表如下:

表2 基控制组构成

计算上述基控制组转矩可达集的体积,以及三轴力矩与转矩可达集的交点,列表如下:

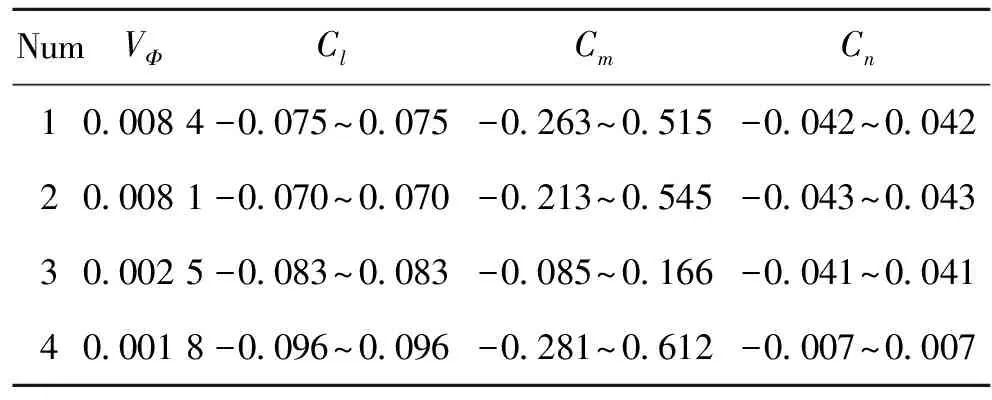
表3 基控制组可达力矩集构成

从表3可以看出,1号、2号基控制组均取得了较大的转矩可达集,1号基控制组与2号基控制组的区别在于:1号基控制组能够取得更大的低头力矩,而2号基控制组能够取得更大的抬头力矩。3号、4号基控制组的转矩可达集虽然较小,但能够获得较大的滚转力矩。

从隐身能力上来看,飞机的前缘襟翼横跨整个机翼前缘,当其发生角度变化时,与机翼产生的凹腔结构,将导致雷达反射大大增强,因此前缘襟翼作为常规控制面不利于隐身。综合考虑各个基控制组的优缺点,选择具有最大转矩可达集体积的1号基控制组(升降舵+副翼+方向舵)作为主控制组,2号、3号和4号控制组按优先级排序作为备用控制组。当副翼发生故障时,采用2号控制组;当升降舵发生故障时采用3号控制组;当方向舵发生故障时采用4号控制组。从表3还可以看出,方向舵对飞机航向的作用非常显著,没有方向舵参与航向控制时,仅能取得0.001 8的转矩可达集,此时Cn跨度仅为-0.007～0.007。

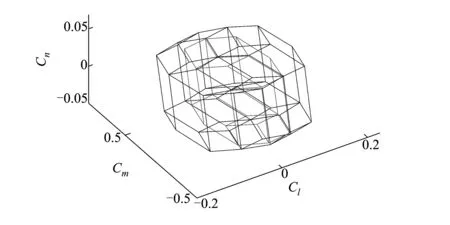
图4 包含辅助操纵面的转矩可达集结构图

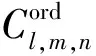
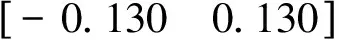
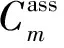
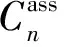
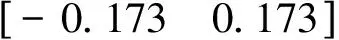
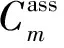
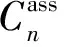
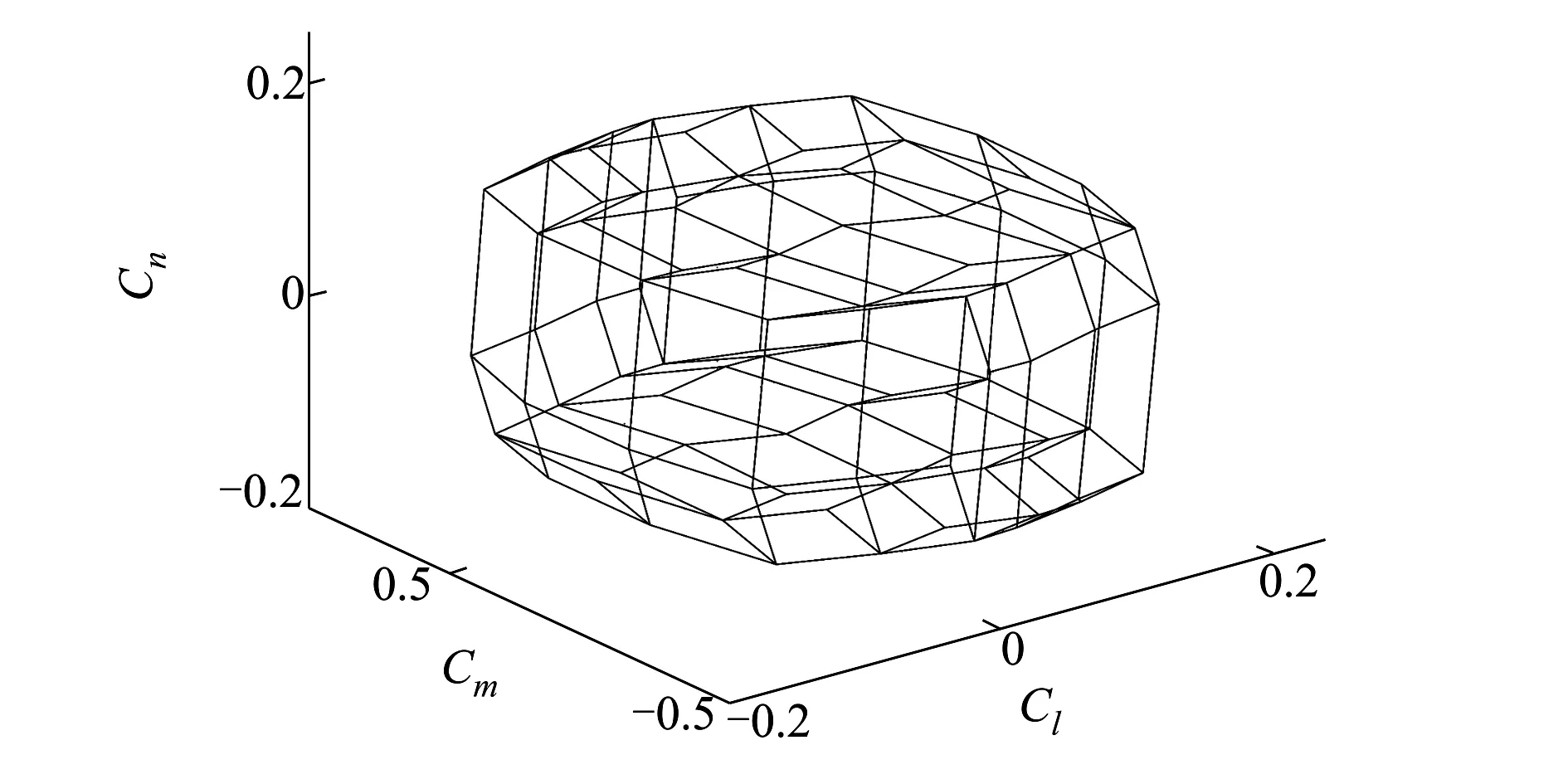
图5 分配系统AMS几何构造

根据AMS的几何构造,我们可以计算出在给定期望力矩时,操纵面的的分配情况。例如当期望力矩v=[0.164 5,-0.020 2,-0.127 2]T时:

1) 若仅使用主控制组,在该矢量方向所能取得的最大力矩为:v=[0.059 3,0.007 3,-0.045 8]T,对应的控制量为

2) 若加入襟翼,则在该矢量方向所能取得的最大力矩为v=[0.060 8,0.007 5,-0.047 0]T,对应的控制量为

3) 若加入推力矢量操纵面,则可实现对期望力矩的完全分配,此时对应的控制量为:

5 结 论

本文首先对转矩可达集的求解进行了研究,通过分析转矩可达集的几何构造,对求解中的几个难点进行了详细解释,并推导了转矩可达集的计算公式。通过探讨先进战斗机各飞行阶段对于操纵面分配的要求,以及欧美先进战斗机对于操纵面的实际使用和分配情况,给出了“确立主控舵面,其它舵面为辅”的操纵面组合分配设计思路。在具体实施时,首先根据各个基控制组转矩可达集的大小及其偏转的阻力特性、雷达反射特性确立主控舵面,当主控舵面不能满足飞行对于可用力矩的需求时,启用其他辅助操纵面及推力矢量操纵面。随后的仿真算例验证了本文提出的方法对于多操纵面分配方案设计及转矩可达集求解的有效性。

参考文献：

[1] 杨恩泉, 高金源. 先进战斗机控制分配方法研究进展[J]. 飞行力学, 2005, 23(3):1-4

Yang Enquan, Gao Jingyuan. Research and Development on Advanced Fighter Control Allcoation Methods[J]. Flight Dynamics, 2005, 23(3):17-19 (in Chinese)

[2] 王美仙, 李明. 先进战斗机控制分配方法研究综述[J]. 飞机设计, 2006(3): 17-19

Wang Meixian, Li Ming. Development of Advanced Fighter Control Allocation Methods[J]. Aircraft Design, 2006(3): 17-19 (in Chinese)

[3] William C Reigelsperger, Siva S Banda. Nonlinear Simulation of a Modified F-16 with Full-Envelope Control Laws. Control Engineering Practice, 1998(6): 309-320

[4] 史静平, 章卫国, 李广文, 刘小雄. 小生境遗传算法在广义逆控制分配法中的应用[J]. 系统仿真学报, 2009, 21(20): 6593-6596

Shi Jingping, Zhang Weiguo, Li Guangwen, Liu Xiaoxiong. Application of Niche Genetic Algorithm in Optimization of Generalized Inverse Control Allocation Method[J]. Journal of System Simulation, 2009, 21(20): 6593-6596 (in Chinese)

[5] Bordignon K A. Constrained Control Allocation for Systems with Redundant Control Effectors[D]. Virginia Polytechnic Institute and State University, 1996

[6] 史静平, 章卫国, 李广文, 刘小雄. 再分配伪逆法分配效率研究[J]. 中国科学:信息科学, 2010, 53(2): 271-277

Shi Jingping, Zhang Weiguo, Li Guangwen, Liu Xiaoxiong. Research on Allocation Efficiency of the Redistributed Pseudo Inverse Algorithm[J]. Science China Information Sciences, 2010, 53(2):271-277 (in Chinese)

[7] Durham W C. Constrained Control Allocation: Three Moment Problem[J]. Journal of Guidance, Control, and Dynamics, 1994,17(2): 330-336

[8] Durham W C. Attainable Moments for the Constrained Control Allocation Problem[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(6): 1371-1373

[9] Durham W C. Computationally Efficient Control Allocation[J]. Journal of Guidance. Control and Dynamics, 2001, 24(3):519-524

[10] Petersen John A M, Bodson Marc. Constrained Quadratic Programming Techniques for Control Allocation[J]. IEEE Transactions on Control Systems Technology. 2006, 14(1):91-98

[11] 杨恩泉, 高金源, 李卫琪. 多目标非线性控制分配方法研究[J]. 航空学报, 2008, 29(4):995-1001

Yang Enquan, Gao Jinyuan, Li Weiqi. Research on Multi-Object Nonlinear Control Allocation Method[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(4):995-1001 (in Chinese)

[12] 杨凌宇, 范彦铭, 邵山,等. 基于基排序法的冗余操纵面控制分配与管理[J]. 中国科学:技术科学, 2010, 40(4):399-406

Yang Linyu, Fan Yanming, Shao Shan, et al. Control Allocation and Management of Redundant Control Effectors Based on Bases Sequenced Method[J]. Science China Technological Sciences, 2010, 40(4): 399-406 (in Chinese)

[13] Addington G A, Myatt J H. Control Surface Deflection Effects on the Innovative Control Effectors Design[R]. AFRL-VA-WP-TR-2000-3027