基于条纹丢失补偿的自混合干涉位移测量算法

叶会英，朱君瑶，王珍雪

(郑州大学 信息工程学院，河南 郑州450001)

0 引言

光反馈自混合干涉(OFSMI)(即自混合干涉)是指激光器输出光经外部反射体反射或散射后，其中一部分光又反馈回激光器谐振腔，反馈光与腔内光相混合，从而调制激光器输出光［1］． 由于OFSMI 信号携带了外部反射体和激光器自身参数的信息，并且系统装置简单，所以近年来很多学者应用光反馈自混合干涉系统对物体位移［2-4］、距离［5］、速度［6］、加速度［7］及激光器自身参数［8］等的测量进行深入的研究．

笔者基于Lang-Kobayashi 方程建立的OFSMI数学模型［9］:

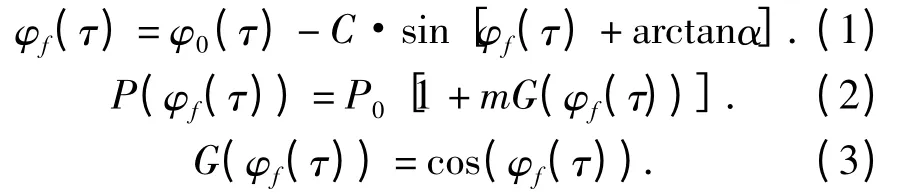
式中:α 是半导体激光器线宽展宽因数;φ0(τ)=ω0τ，φf(τ)=ωfτ;ωf(τ)、ω0(τ)分别是有光反馈和无反馈时激光的角频率;φf(τ)、φ0(τ)分别为有光反馈和无光反馈时的激光器外腔相位;τ =2L/c，L 是外腔长度，c 是光速;C 是光反馈水平因子;P(φf(τ))和P0分别是有光反馈和无光反馈时半导体激光器的输出功率;m 为调制系数(典型值为m≈10-3);G(φf(τ))是干涉函数，它体现了外腔光相位对激光输出功率的影响．

C 是模型中的重要参数，当C ＜1 时，光反馈水平较弱，为弱光反馈;当1 ＜C ＜4．6 时，为适度光反馈;在弱光反馈和适度光反馈的情况下不会出现条纹丢失现象，此时可利用条纹计数法来测量物体的位移;当C ＞4．6 时，为强光反馈，此时会出现条纹丢失现象［10］．本文研究C ＞4．6 条件下的条纹丢失规律，并进行条纹丢失补偿算法的研究，提高测量的精度．

1 条纹丢失规律

通过对高反馈水平因子条件下的自混合干涉信号进行行为分析［11］，发现当C ＜1 时，φ0和φf成一一对应的关系，此时OFSMI 信号为正弦波信号，和传统干涉条纹一致;当1 ＜C ＜4．6 时，φ0和φf之间的关系变得比较复杂，一个φ0对应着3 到5 个φf，此时OFSMI 信号为锯齿波信号;当C ＞4．6时，一个φ0对应5 个甚至更多φf，如图1 所示，此时，OFSMI 信号会出现条纹丢失现象．

设外部物体做正弦波运动，研究高反馈水平因子条件下的自混合干涉条纹丢失规律的步骤:

第一步，选取φf=19，即外腔的移动位移为一个定值，然后分别令C =4，4．7，4．8，5，6，7．9，8，9，所对应的OFSMI 信号如图2 所示．从图2 中可以得出，对于确定的φf值，φf=19，在半个周期内条纹的数目N 随C 值的变化情况:当C ＜4．8时，N=6;当4．8≤C ＜5 时，N =5;当5≤C ＜7．9时，N=4;当7．9≤C ＜9 时，N=3．

图1 当C=0．5，3 ，10 时，φf与φ0的关系Fig．1 Relationship between φf and φ0where C=0．5，3，10

第二步，改变φf的值，取φf=25，按照上述的方法，令C =4，4．7，4．8，5，6，7．9，8，9，所对应的OFSMI 信号如图3 所示．从图3 可以得出，当C ＜4．6 时，N=8;当4．6≤C ＜4．8 时，N=7;当4．8≤C ＜7．9 时，N=6;当7．9≤C ＜9 时，N=3．

在实验中，物体位移最大约10 μm，对应的外腔相位变化最大约160 rad，所以在φf为(0，160)的范围内，随机取100 个值，按照上述的方法研究在半个周期内，条纹丢失数目m 随着C 的变化规律为:C ＜4．6，m=0;4．6≤C ＜4．8，m=1;4．8≤C＜7．9，m=2．

图2 φf =19 时C 取不同值对应的OFSMI 信号Fig．2 Simulated OFSMI signals with different C values corresponding to φf =19

图3 φf =25 时C 取不同值对应的OFSMI 信号Fig．3 Simulated OFSMI signals with different C values corresponding to φf =25

2 位移重构

光反馈自混合干涉的基本规律是:当φf(τ)有2π 相位的变化(即外腔移动半个光波波长λ0/2)时，则G(τ)产生一个周期波动的信号，称之为一个整数条纹;小于2π 相位的φf(τ)的变化，所产生的G(τ)变化量，称之为小数条纹． 因此把φf(τ)的变化Δφf(τ)分为两部分，记做:Δφf(τ)=AI+AD． 其中，AI为整数干涉条纹所对应的相位，AI=2Nπ，N 为整数条纹的个数;AD为小数条纹所对应的相位．物体位移D(t)与外腔相位变化量Δφf(τ)之间的关系为［12］

D(t)=Δφf(τ)×λ0/(4π)． (4)

利用锯齿段的最小二乘线性拟合，可得出小数条纹G(AD)表达式为［13］

G(AD)= -0．95 +0．39AD． (5)

由实验的自混合干涉信号测得G(nA)和G(nB)如图4 所示．

图4 外腔正弦振动信号及其对应的自混合信号Fig．4 Sinusoidal displacement of an external object OFSMI signal

把G(nA)和G(nB)代入G(AD)，可计算出相应的小数相位，分别记做ADA和ADB，则一个小数条纹所对应的相位为(ADA+ADB)/2．

在适度光反馈及强光反馈下，利用条纹计数法测量物体位移时，把得到的OFSMI 信号进行微分处理，得到正负脉冲信号D(n)，如图5 所示．图中正脉冲表示物体沿正方向移动，负脉冲表示物体沿反方向移动．在没有考虑条纹丢失情况时，位移算法的流程图为图6［14］．

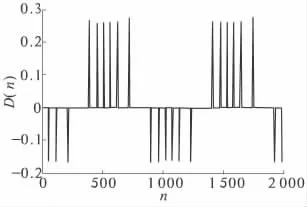
图5 OFSMI 信号进行微分得到的正负脉冲信号Fig．5 Differential signal of the OFSMI signal

用s(n)表示检测到的脉冲信号的正负，n 表示检测到的脉冲数目，n =1，2，3，… ． 当s(n)=1，表示检测到的第n 个条纹是正脉冲;s(n)=-1，表示检测到的第n 个条纹为负脉冲．

对正负脉冲信号进行检测，当s(n)等于s(n-1)，表示脉冲的方向没有发生改变，此时用s(n)* 2π 表示，输入到累加模块中;当s(n)不等于s(n-1)，表示脉冲的方向发生改变，则表示为s(n)* ［2π +(ADA+ADB)/2］，(ADA+ADB)/2 表示一个小数条纹代表的相位，输入到累加模块中，把累加模块中的数据求和，然后乘上λ0/(4π)得到物体的移动位移D(t)．

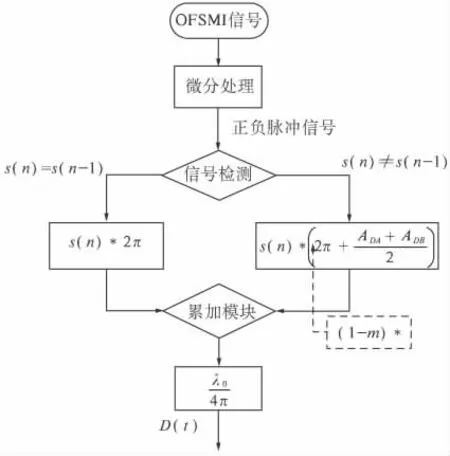
图6 未考虑条纹丢失的位移算法Fig．6 The displacement algorithm without considering the fringe-loss

为提高条纹计数法测位移的精度，则需考虑条纹丢失并进行条纹丢失补偿，重构位移算法的模式加入虚框图中的系数．

当检测到的s(n)不等于s(n -1)，表示检测到的脉冲信号的方向发生改变，此时要对丢失的条纹进行补偿，有s(n)* ［(1 +m)* 2π+(ADA+ADB)/2］，m 表示半个周期内条纹丢失的数目，输入到累加模块中，把累加模块中的数据求和，然后乘上λ0/(4π)得到物体的位移D(t)．

3 实验结果

在仿真实验中，分别取C =4．7 和C =7 时，对算法1(未考虑条纹丢失所测位移)和算法2(考虑条纹丢失并进行补偿所测位移(位移重构))进行对比，如表1 所示．

从表1 可得出，在未考虑条纹丢失时，所测得的物体的移动位移与实际位移相差较大，精度不高;考虑条纹丢失现象并进行补偿时，测得的物体的移动位移与物体的实际位移相差约0 ～0．2 μm，测量的精确度有了很大的提高． 笔者提出的算法更适合用于条纹计数法测量物体的位移．

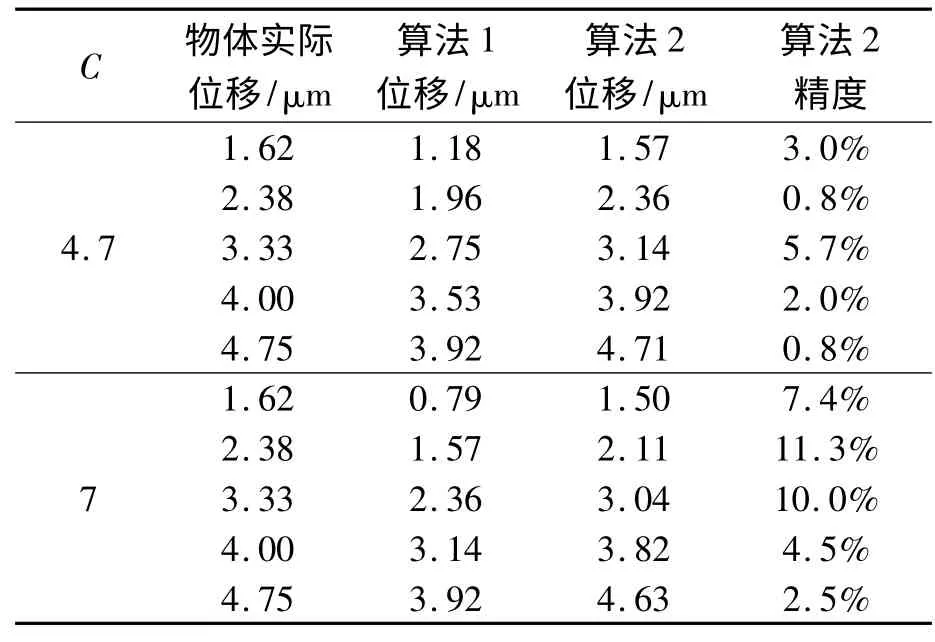
表1 C=4．7，7 时算法1 和算法2 的比较Tab．1 Comparison of algorithm 1 and 2 with C=4．7，7

4 结束语

在高反馈水平因子条件下，会出现条纹丢失现象，此时利用条纹计数测位移的精度比较低．本文研究了在0 ＜C ＜7． 9 范围内，条纹丢失的条数，并在重构位移时进行条纹丢失补偿，同时本文提出的算法考虑到小数条纹所代表的位移，使得测得的物体位移更精确，为下一步高光反馈水平因子条件下的其他研究奠定了基础．

［1］ 赵岩，禹延光，叶会英． 基于光反馈自混合干涉的对称折叠算法的精度分析［J］． 激光技术，2009，33(4):387 -390．

［2］ 杨振宇，王鸣，夏巍，等． 正弦相位调制自混合干涉大范围位移测量精度测试与分析［J］． 光学学报，2013，33(4):0412007(1 -7)．

［3］ 杨颖，李醒飞，寇科，等． 全相位谱分析在自混合干涉位移测量中的应用［J］． 光学精密工程，2012，20(8):1740 -1746．

［4］ ZABIT U，BERNAL O D，BOSCH T． Mixing laser sensor for large displacement signal recovery in the presence of speckle［J］． IEEE Sensor Journal，2013，13(2):824 -831．

［5］ 胡险峰． 用激光二极管自混合干涉测量距离［J］．物理实验，2013，33(1):26 -29．

［6］ 张照云，高杨，赵兴海，等． 半导体激光自混合变速测量的离散Chirp -Fourier 变换方法［J］． 红外与激光工程，2012，41(4):1074 -1077．

［7］ 杨颖，李醒飞，李洪宇，等． 基于激光自混合效应的加速度传感器［J］． 光学学报，2013，33 (2):0228003(1 -7)．

［8］ 张玉燕，胡伟，监雄，等． 一种自混合干涉位移测量系统中参数C 的测量方法［J］． 光电子·激光，2013，24(6):1150 -1157．

［9］ BES C，PLANTIER G，BOSCH T． Displacement measurements using a self-mixing laser diode under moderate feedback［J］． IEEE Transactions on Instrumentation and Measurement，2006，55(4):1101 -1105．

［10］ZABIT U，BONY F，BOSCH T． A self-mixing displacement sensor with fringe-loss compensation for harmonic vibrations［J］． IEEE Photonics Technology Letters，2010，22(3):410 -412．

［11］ YU Yan-guang，XI Jiang-tao． Optical feedback selfmixing interferometry with a large feedback factor C:behavior studies［J］． IEEE Journal of Quantum Electronics，2009，45(7):840 -848．

［12］MAGNANI A，NORGIA M，PESATORI A． Optical displacement sensor based on novel self-mixing reconstruction method［C］//IEEE SENSORS 2010 Conference．Kona，KI:IEEE Press． 2010:517 -520．

［13］禹延光，郭常盈，叶会英． 基于适度光反馈自混合干涉技术的振动测量［J］． 光学学报，2007，26(8):1430 -1434．

［14］ SERVAGENT N，GOUAUX F，BOSCH T． Measurements of displacement using the self-mixing interference in a laser diode［J］． Optical，1998，29(6):168 -173．