多用户多进制FM-DCSK 误码率分析

刘 平，李 宁，邢军阳

(郑州大学 信息工程学院，河南 郑州450001)

0 引言

混沌信号以其类随机性、良好的互相关、自相关等统计学特性在混沌扩频通信领域获得了飞速的发展［1］． 比较突出的有混沌键控(CSK)、差分混沌键控(DCSK)、频率调制差分混沌键控(FMDCSK)［2-3］．Carroll 和Pecora 提出了多路传送的混沌信号技术，并且将混沌映射产生的扩频码用于传统的CDMA 通信系统中［4］． Kennedy 等［5］提出了多路差分混沌键控系统(MA-DCSK)．多路频率调制差分混沌键控(MA-FM-DCSK)的性能已经被Jako 等人深入研究［6］．笔者提出一种多进制和Walsh 码相结合的多用户FM-DCSK 混沌通信系统，并且分析了在多用户情况下的系统性能，给出了误码率公式．

1 MAMA-FM-DCSK 系统原理

假设在MAMA-FM-DCSK 系统中有N 个用户，第k 个用户的发送端原理图如图1 所示．

在发送端输入的二进制序列经过分组映射后变成多进制码元序列．对每一个L 进制信息码元，假设多进制FM-DCSK 调制系统的扩频系数为2M，即在每个码元周期内，参考段和信息段各包含M个混沌基函数xki．根据发射多进制码元的不同，信息序列为，bl为传输码元，在多进制系统中，bl∈(±1，±3，……，±(L -1))．笔者讨论第k 个用户的第1 个发射码元．用户k 的发射信号为

式中:M 为扩频系数;i 为第i 个混沌基函数;bk1 为第k 个用户发射的第1 个发射码元;wki 为长度为M 的Walsh 码序列．

系统中有N 个用户，发送端发射的信号为

假定信道噪声为高斯白噪声，发射端叠加高斯白噪声ζi，所以输入解调器的信号为

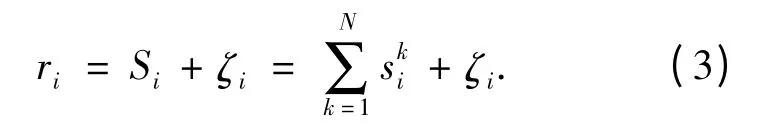
由于ζi为平稳随机高斯过程，所以对任意i≠j，ζi和ζj是统计独立的;其双边功率谱密度为N0/2．

用户k 的接收端原理图如图2 所示． 图2 中输入信号延迟半个码元周期后与未延迟信号以及Walsh 码相乘，该组Walsh 码与用户k 在发送端叠加的Walsh 码相同，则接收机的相关器的输出为

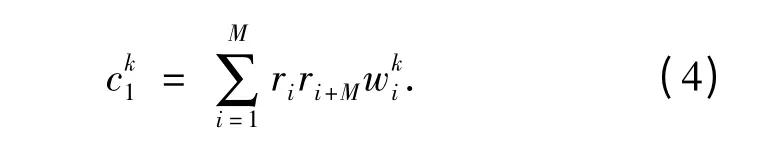
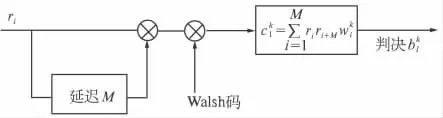
图2 接收端原理图Fig．2 The schematic diagram of sending side

将式(2)和式(3)代入式(4)中，可以得到:

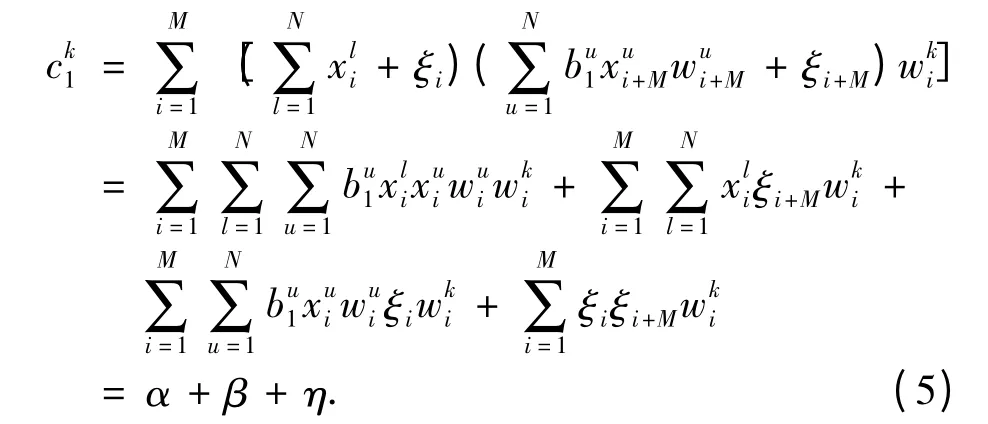
根据Walsh 码的正交性和ζi的统计特性，并且FM-DCSK 调制中码元能量Eb恒定，即

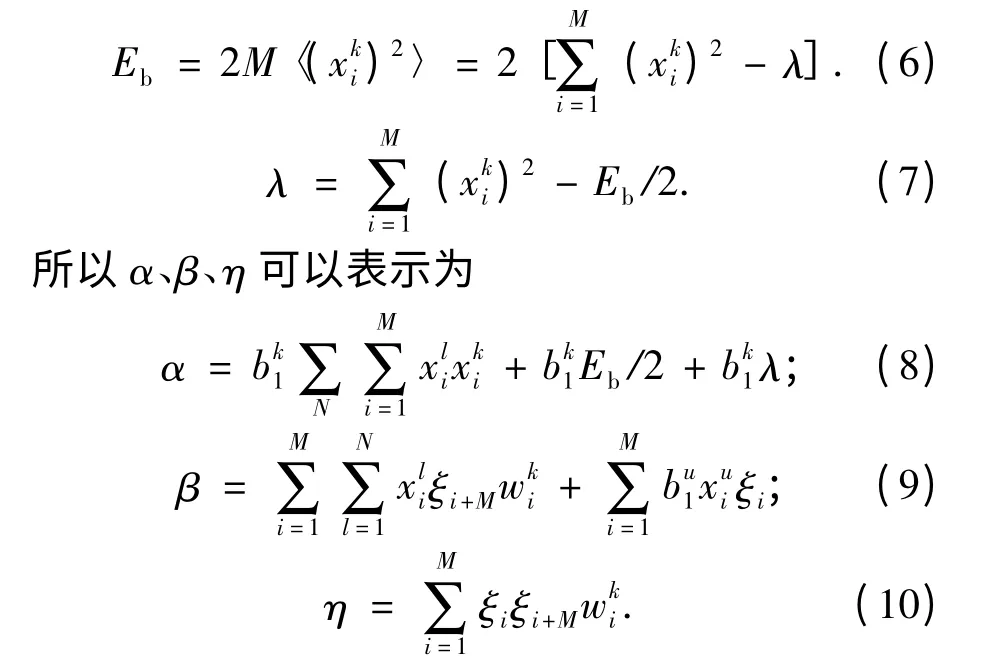
式(8)中第一项为多用户干扰项，β 和η 为噪声干扰项，bk1λ 为误差干扰项． 所以式(5)可以表示为

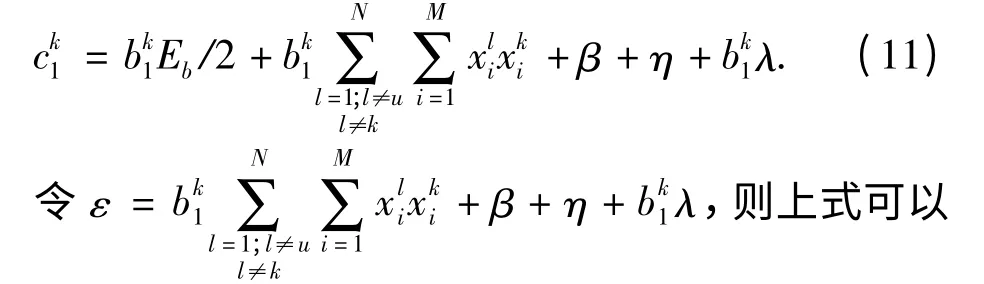
其中，Z 为接收机相关器输出．

式(5)中多用户干扰和噪声干扰非常严重，引入Walsh 码以后，由于Walsh 码的正交性消除了大部分干扰，如式(11)所示．对于二进制系统，相关器输出的判决门限为零;而多进制系统由于发送多个电平，如式(12)所示，所以其判决门限根据发送码元的不同而不同［7］．

2 MAMA-FM-DCSK 系统性能分析

在本文的分析中，使用零均值Logistic 映射产生混沌序列． 零均值Logistic 映射为xk+1=1 -其概率密度方程为ρ(y)=1/π;方差为1/2．

根据文献［8］，误差干扰项λ 的方差为

对于多进制系统，判决门限应该为(0，±2，…，±(L-2));所以相邻电平间隔为2d=Eb．当噪声抽样值＞d 时，将发生错判．例外情况是，当发送电平为+(L -1)时，ε ＞+d 时不会发生错判;当发送电平为-(L -1)时，ε ＜-d 时也不会发生错判． 由于每个电平都是等概率发送，所以多进制系统的平均误码率为

由于ξi为均值为零，方差为σ2的高斯白噪声;xi为混沌序列，当扩频系数M 足够大时，xi近似为高斯随机过程． 所以，ε 也为高斯随机过程．式(14)可以表示为

式中:d 为电平间隔;σn为干扰项ε 的方差;erfc(* )为互补误差函数．

由于对任意i≠j，ζi和ζj，xi和xj，ζi和xi都是统计独立的．ζi双边功率谱密度为N0/2;xi的方差为式，wi的方差近似为1［9］．所以

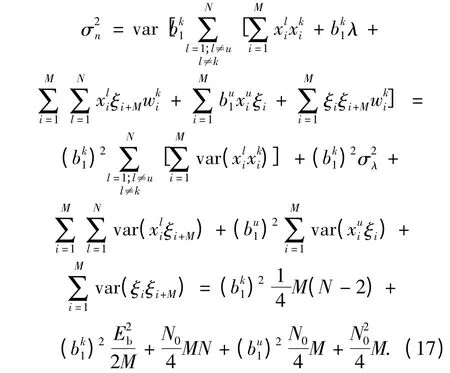
由于bl等概率发送，所以式(17)中第一项，第二项和第四项是变动的，b2l 的平均值可以表示为

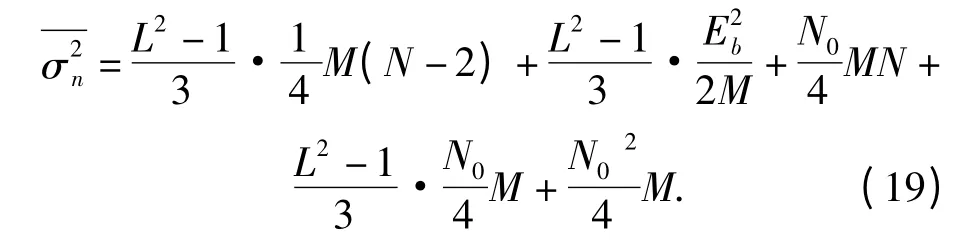
因为Eb=2M≈2Mvar(xi)，var(xi)=;所以Eb=M．

将式(19)和电平间隔表达式2d =Eb代入式(16)得新系统的误码率为

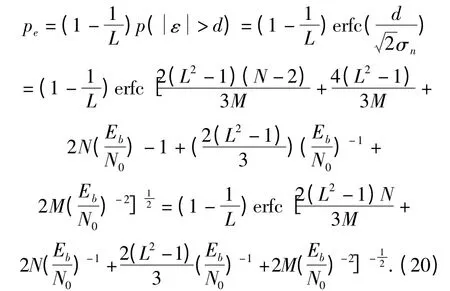
图3 表示N 不同时的误码率情况，在本次仿真中L=4，扩频系数M =100，分别对N =2，3，4进行仿真分析．多用户多进制通信系统比单用户二进制通信系统误码率有较大的增加，这是因为多进制判决门限增加，且判决门限不为零，增加了系统误码率．另外，随着用户数目的增加，误码率也有明显的增加，这是因为用户数目的增加，多用户之间的干扰增加，造成了误码率的上升．

图4 为改变电平间隔后不同用户数目的误码率情况．在图4 的仿真中电平间隔d =Eb/2，当增加电平间隔至d =/2 时，仿真结果见图4．从图4 可以看出，适当增加电平间隔能显著地改善系统性能．但是，增加电平间隔将会在发送端需要更多的发射功率，所以，电平间隔不能无限制地增加．

图5 为当用户数目N =3 时，不同进制的误码率情况．选取N =3，扩频系数M =100，分别对L=2，3，4 进行仿真． 从图5 可以看出，当L 增加

当L=2，N =1 时上式为单用户二进制FMDCSK 误码率，单用户二进制FM-DCSK 误码率由文献［10］给出．

3 仿真结果及分析

仿真结果表示在图3 ～5 中，其中仿真值表示仿真结果，理论值表示利用式(21)仿真得到的理论结果，传统多用户二进制FM-DCSK 误码率公式由文献［11］给出．是误码率明显上升，主要是由于L 增加，判决门限数目增加，由此造成了误码率的上升．

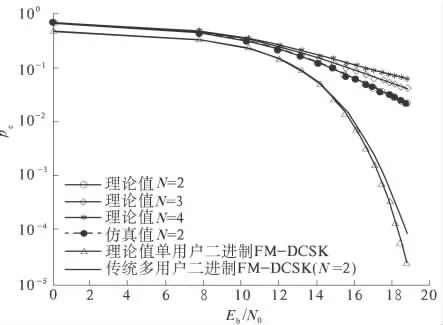
图3 N 不同时的误码率情况Fig．3 The BER with different N

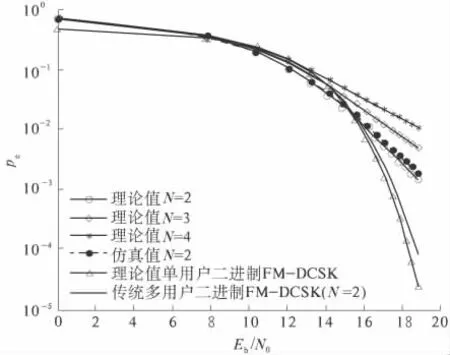
图4 改变电平间隔后N 不同时的误码率Fig．4 The BER with different N and different level interval

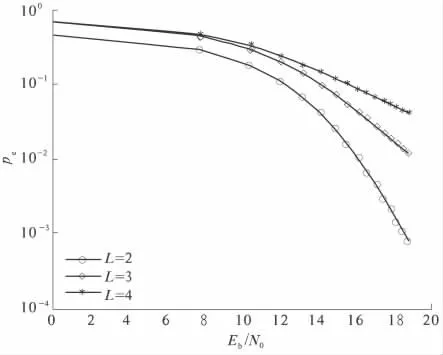
图5 N=3 时，不同进制的误码率情况Fig．5 N=3，The BER with different multi-system

4 结论

笔者提出了一种新的多用户多进制FM-DCSK 混沌通信系统，并且在系统中利用Walsh 码，大大降低了多用户之间的干扰;详细地分析了新系统的原理性能，并给出了误码率公式;并且通过仿真验证了系统的性能． 新系统在基本不增加系统复杂性的同时，大大提高了二进制码元传输效率;同时，其误码率相比传统多用户系统仅有略微增加．通过选取适当的电平间隔，误码率将得到显著的改善．由于篇幅限制，只讨论了理想信道下的误码率;当信道噪声影响到Walsh 码的正交性时，误码率将会显著增加，所以下一步工作将致力于实际环境条件下系统性能的研究．

［1］ KOLUMBAN G，KENNEDY M P，CHUA L O． The role of synchronization in digital communications using chaos (Part I):Fundamentals of digital communications［J］． IEEE Trans Circuits Syst I，1997，44(8):927 -936．

［2］ HERVE D，MICHAEL P K，MARTIN H． Chaos shift keying:modulation and demodulation of a chaotic carrier using self-synchronizing chua’s circuits［J］． IEEE Transactions on Circuits and Systems II:Analog and Digital Signal Processing，1993，40(10):634-642．

［3］ KOLUMBAN G，KIS G，JAKO Z，Michael Peter Kennedy FM-DCSK:A Robust modulation scheme for chaotic communications［J］． IEICE Trans． 1998，E81(9):1798 -1802．

［4］ CARROLL T L，PECORA L M． Using multiple attractor chaotic systems for communication［J］． Chaos:An Interdisciplinary Journal of Nonlinear Science．1999，9(2):445 -451．

［5］ KENNEDY M P，KOLUMBAN G，JAKO Z． Recent advances in communicating with chaos［C］//IEEE International Symposium on Ciruits and Systems．Monterey，CA，USA:IEEE Press，1998:461 -464．

［6］ JAKO Z，KIS G，KOLUMBAN G． Multiple access capability of the FM-DCSK chaotic communications system［C］//NDES2000，Catania，Italy． 2000:52 -55．

［7］ 樊昌信，曹丽娜． 通信原理［M］． 6 版．北京:国防工业出版社，2006:205 -207．

［8］ CHERNOV N I． Limit theorems and markov approximations for chaotic dynamical systems［J］． Probability Theory and Related Fields，1995，101(3):321-362．

［9］ 周志波，周童，王进祥． 一种改进的多用户DCSK性能分析． 西安电子科技大学学报:自然科学版．2009，36(4):732 -735．

［10］GALIAS Z，MAGGIO G M． Quadrature chaos shift keying:theory and performance analysis［J］． IEEE Transactions on Circuits and Systems，2001，48(12):1510 -1518．

［11］李辉． 混沌数字通信［M］． 合肥:中国科技大学出版社，2004:47 -48．