基于AR模型的水电机组振动信号趋势预测

孙慧芳，付婧，郑云峰

（中国水利水电科学研究院，北京 100038）

水电机组是水电能源的关键设备，机组运行状况的好坏直接影响水电站的安全运行。目前，水电机组正朝着高水头、高效率、高转速和大容量的方向发展，随着状态监测与故障诊断技术水平的发展，以及设备管理水平的提高，水电站设备的维修理念以“预防为主，计划检修”的方针开始尝试转变为“预测性维修”的检修模式。由于水电机组的故障信息大部分都通过振动信号来反映，因此对水电机组的振动信号进行趋势预测很有必要。

对振动信号的趋势预测是根据其过去和现在的情况，科学地预测和推断这些信号未来的发展趋势。趋势预测方法一般以时间序列进行数据建模，基本思想是将一列随时间变化又互相关联的数据用相应的数学模型加以近似描述，实现最小方差下的最佳预测。文章对某电站上机架+X向的一段振动数据进行了基于AR模型的趋势预测，计算方法简单，可以满足现场实时性的需求。

1 ARMA模型

时间序列xtΣΣ可以表示为n阶自回归m阶滑动平均混合时序模型，即ARMA(n，m)模型，表达式如下:

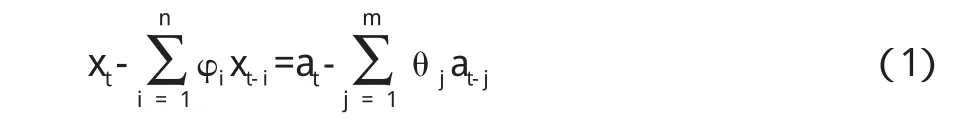
式中，xt为Σ在t时刻的取值；为自回归(Auto-Regressive)参数；θ1=（1，2，……m）为移动平均(Moving Average)参数；at是均值为0，方差为的独立正态分布序列（白噪声）。当n=0时，模型称为纯滑动平均模型MA(m)；当m=0时，模型成为纯自回归模型AR(n)。

由于水电机组的振动复杂性，振动信号一般是非平稳的时间序列，需要经过适当的变换得到平稳的时间序列ARMA(n，m)，为此提出了ARIMA模型:将一个非平稳序列进行差分处理得到平稳时间序列。设Σ为非平稳序列，存在正整数d，使得，t＞d，其中称为d阶差分算子。ARIMA模型实质上是平稳时间序列分析在非平稳情况下的拓展，但其仍基于ARMA分析。

对于ARMA模型和AR模型之间的关系有wold分解定理:任何一个方差有限的平稳ARMA过程都可以表示为唯一的阶数可能无穷大的AR过程。ARMA模型的随机信号总可以化为一定阶数的AR模型，因此AR模型的参数估计在实际问题中应用较广。

2 AR模型的建模

AR模型的建模包括模型的定阶和模型的参数估计，即要估计出自回归参数φi和模型的阶数n。

模型阶数估计的一个常用准则为AIC准则，计算公式如下:

AR模型模型参数估计的方法有很多，如:最小二乘估计法、加权算法和Burg算法等等，文章采用Burg算法。Burg算法的基本思想是对信号进行前向和后向的预测，令前后向预测误差功率之和为最小。MATLAB中有可以实现Burg算法的AR模型参数估计函数[ae]=arburg(xn)，其中a为函数返回的模型系数向量，e为最小预测误差。

参数估计需要预先知道模型阶次，因此建模过程中应先给定模型阶次，按照Burg算法估计模型参数，可以得到各阶模型，最后取最小AIC(n)值对应的阶次来确定模型的最佳阶此，同时也可以确定AR模型。

3 水电机组振动信号的AR建模

取某电站上机架+X向的2000个振动数据进行建模，其序列图见图1所示，可以看出该序列不是平稳序列。对其进行2阶差分，差分后数据自相关系数见表1，自相关系数随着k的增大而逐渐趋向0，证明差分后的序列为平稳时间序列，序列图见图2所示。

按照AR模型的建模方法对差分后的振动数据进行建模，使用Burg算法估计出各阶参数，然后计算相应的AIC值，不同阶数对应的AIC值如图3所示，从图中可知，当n=48时AIC值最小，即最佳模型阶次为48阶。

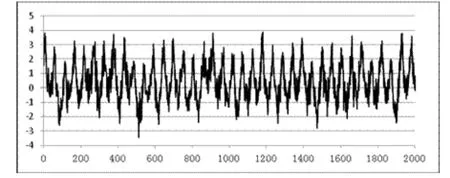
图1 上机架+X向振动信号序列图

图2 上机架+X向振动信号差分后的平稳序列

图3 AR模型在不同阶次下的AIC值

表1 差分后的振动信号自相关系数估计值

以差分后的振动信号数据做AR模型拟合，估算出该平稳信号的估计值，经过相应的反变换得到原始振动信号的拟合模型，并以100个数据作样本预测，预测结果见图4所示。由图4可以看出利用AR模型对水电机组振动信号预测的数据与实际采集到的数据基本一致。

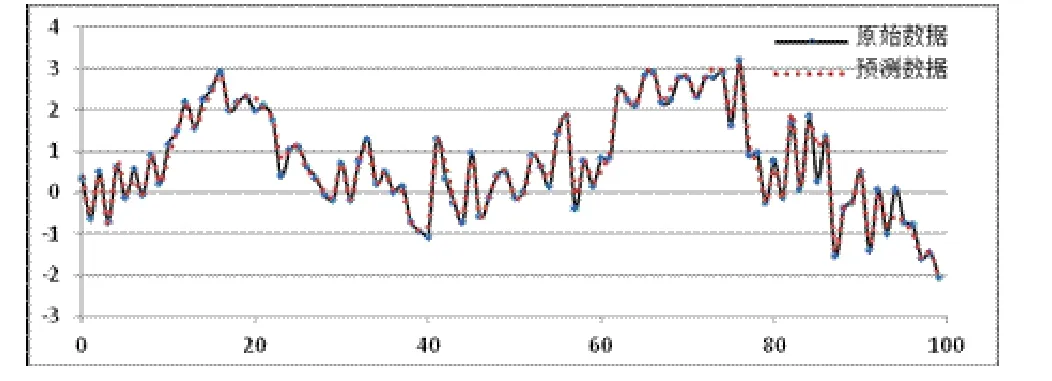
图4 预测值与实际值的比较

4 结语

上述分析说明采用AR模型对水电机组的振动信号进行趋势预测是科学的。但是，该方法在计算过程中存在下列问题:由于水电机组的振动信号是随机的非平稳时间序列，对于个别参数计算过程会经常出现矩阵奇异或近奇异的情形，矩阵求逆可能遇到困难，影响计算精度，因此后续需要对这些问题进行进一步的研究。