大客流地铁车站的设施配置优化模型*

张艳妮张 鹏陈 洪保丽霞

（1.镇江市交通规划设计院，212013，镇江；2.江苏大学汽车与交通工程学院，212013，镇江；3.上海市城市建设设计研究院智能交通研发中心，200125，上海∥第一作者，工程师）

大客流地铁车站的设施配置优化模型*

张艳妮1张 鹏2陈 洪3保丽霞3

（1.镇江市交通规划设计院，212013，镇江；2.江苏大学汽车与交通工程学院，212013，镇江；3.上海市城市建设设计研究院智能交通研发中心，200125，上海∥第一作者，工程师）

针对地铁大客流，建立了以乘客平均密度最小（平均占用空间最大）为目标的设施配置优化模型。该模型是一个整数非线性规划模型，变量是售票设施开放的数目和闸机开放时数。以上海轨道交通1号线上海火车站站为例，对该模型进行了实例验证。结果表明，在大规模客流集中到达情况下，该模型可以使客流均匀分布到枢纽的各个空间区域，有效地提高了地铁车站的服务水平。

地铁；大客流；车站设施；配置优化

First-author'saddressZhenjiang Communications Planning and Design Institute，212013，Zhenjiang，China

城市轨道交通线路的走向一般都是客流集中的交通走廊，连接着重要的客流集散点，如客运枢纽站、商业中心、文体活动中心等。此类站点在节假日或遇有大型活动时常出现客流在某一时段集中到达的情况。客流超过车站正常客运设施所能承担客流量的情况，称为大客流［1］。此时车站内部会非常拥挤并发生乘客滞留现象，如不加以控制不仅会对乘客出行造成不利影响，还会对运营安全造成较大威胁。目前，针对城市轨道交通车站大客流常采用人工的组织方法［2-7］。此类方法依赖人工经验，其组织效果和效率都难以保证。

本文采用运筹学的理论建立了使滞留旅客均匀分布的大客流组织数学模型，考虑合理调节地铁车站客流服务设施的工作数量（如自动售票机、闸机等），以达到滞留乘客流均匀分配到各个空间区域（购票空间、进站排队空间和站台等候空间）的目的。并以上海轨道交通1号线的上海火车站站为例，对该模型进行了验证。

1 模型的建立

1.1 约束条件

进入地铁枢纽的客流一般都有专用且独立的购票空间、进站排队空间和站台等候空间，3个空间的乘客密度不应超过一个上限（称为最大乘客密度）。当到达乘客流量小于服务设施的消散能力时，乘客一般会顺畅地通过，不会发生排队滞留现象；当到达乘客流量大于服务设施的消散能力时，则会发生乘客排队滞留现象。

1.1.1 购票区的约束条件

假设购票区的有效排队空间为A1（空间以m2计，下同），初始时刻滞留在购票区的乘客数为P0，A1（乘客数以人计，下同），则初始乘客密度为：

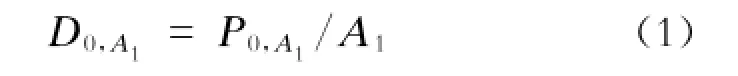
列车到达间隔周期t内乘客平均到达流率为V1（流率以人/min计，下同），t内购票区乘客数为

Pt，A1，则此时乘客密度Dt，A1不应超过一个上限：

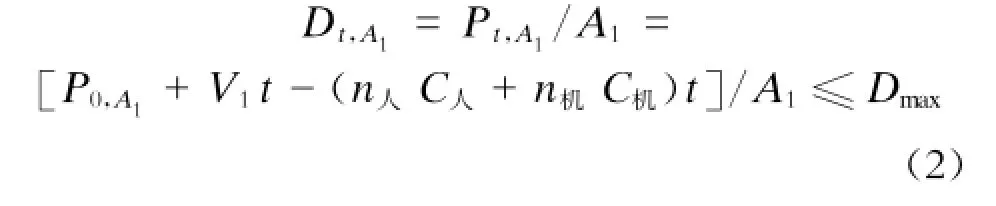
式中：

C人——1个人工售票窗口的服务能力（服务能力以人/min计，下同）；

C机——1个自助售票机的服务能力；n人——开放的人工售票窗口的个数；n机——工作中自动售票机的个数；Dmax——乘客密度的上限。

随着时间推移，乘客密度不断增大，本文用平均密度表示这个时段乘客的平均占用空间情况：

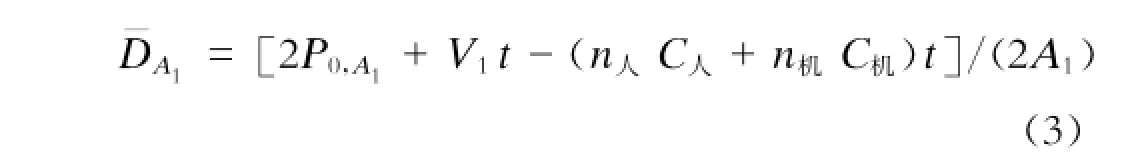
1.1.2 检票区的约束条件

假设检票区的有效排队空间为A2，初始时刻滞留在购票区的乘客数为P0，A2，则初始乘客密度为：

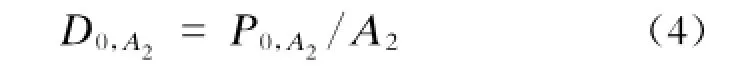
列车到达间隔周期t内的检票区乘客平均到达流率为V2，t内检票区的乘客数为Pt，A2，则此时的乘客密度Dt，A2不应超过一个上限：

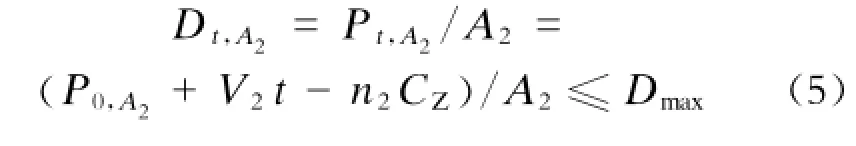
式中：

CZ——1个闸机的服务能力；

n2——闸机服务的总时数（即在研究时段内所有闸机服务时间的总和，以min为单位）。

则t时段末总的客流消散为n2CZ。检票旅客到达流率V2=n人C人+n机C机+V充（式中，V充为持有充值卡不需要购票的乘客流率）。

可见，随着时间的推移，乘客密度是不断增大的，可用平均密度来表示这个时段乘客的平均占用空间情况：

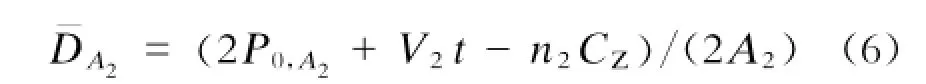
1.1.3 站台候车区的约束条件

站台形式（常用侧式站台和岛式站台见图1）的不同，站台候车区的客流密度表达也不同。

1.1.3.1 侧式站台

设侧式站台一侧候车站台的有效排队空间为A3，初始时刻滞留在站台区的乘客数为P0，A3，则初始乘客密度为：

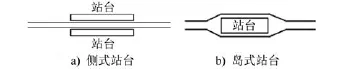
图1 侧式站台和岛式站台

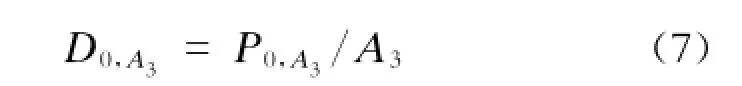
时间为t内的乘客的密度Dt，A3不应超过一个上限：

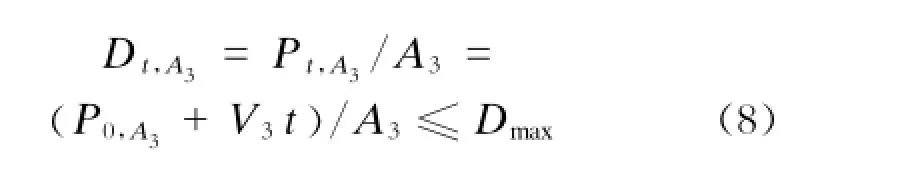
式中：

V3——一侧站台乘客到达流率，V3=n2·CZ/t。

一侧站台乘客平均密度为：

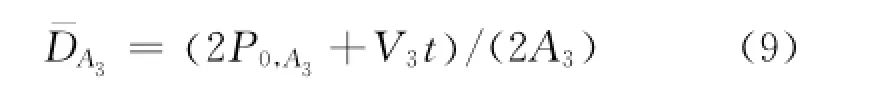
1.1.3.2 岛式站台

本文将岛式站台分为上行乘客候车区和下行乘客候车区。这2个区域共用相同的售票和进站闸机设施。当只有1个候车区（如上行候车区）出现乘客滞留时，设上行候车站台的有效排队空间为A上，初始时刻滞留在站台区的乘客数为P0，A上，则其初始乘客密度为：

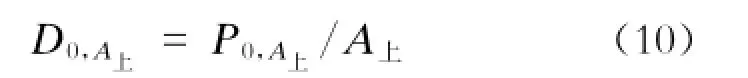
时间t内乘客的密度Dt，A上不应超过一个上限：

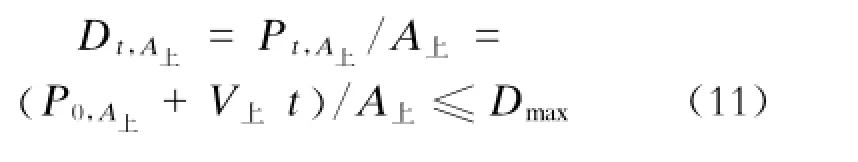
式中：

V上——上行站台乘客到达流率，V上=（n2CZ/t）·α。

α——上行到达乘客占总到达乘客的比例。上行站台乘客平均密度为：

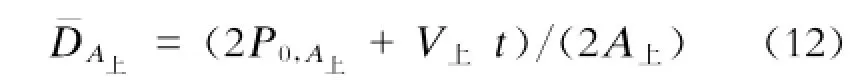
当上行候车区和下行候车区都发生乘客滞留时，设下行候车站台的有效排队空间为A下，初始时刻滞留在站台区的乘客数为P0，A4，则其初始乘客密度为：

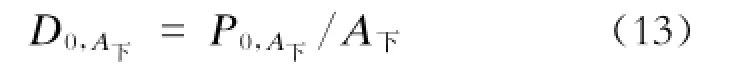
时间t内的乘客密度不应超过一个上限：

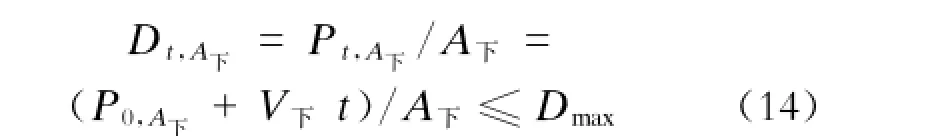
式中：

V下——下行站台乘客到达流率，V下=

（n2CZ/t）（1-α）。

下行站台乘客平均密度为：

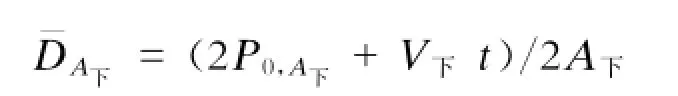
1.2 目标函数

对侧式站台而言，在时间t内应综合考虑乘客排队购票、排队检票和站台候车，3个空间的乘客平均密度的加权算术平均值最小为目标函数：

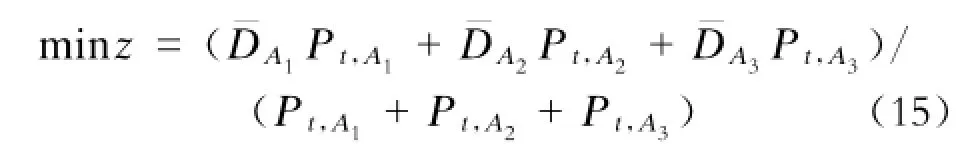
对岛式站台而言，如果一侧站台（如上行方向）发生滞留，在时间t内应综合考虑乘客排队购票、排队检票和站台候车，3个空间的乘客平均密度为其加权算术平均值最小为目标函数：

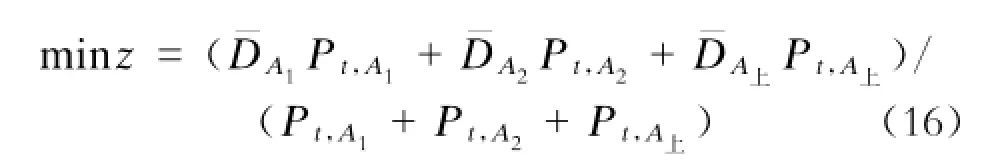
如果两侧站台均发生滞留，则：

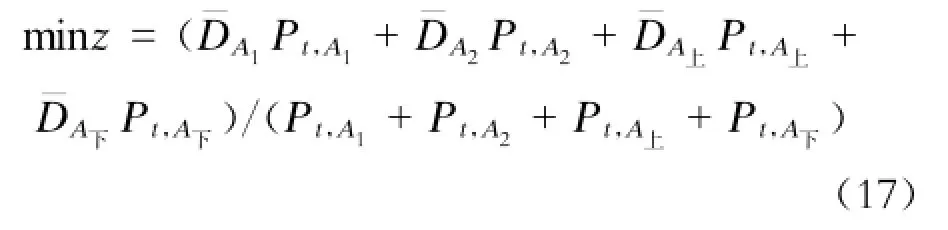
1.3 模型的建立

对侧式站台，以乘客平均密度最小（平均占用空间最大）为目标的模型如下：

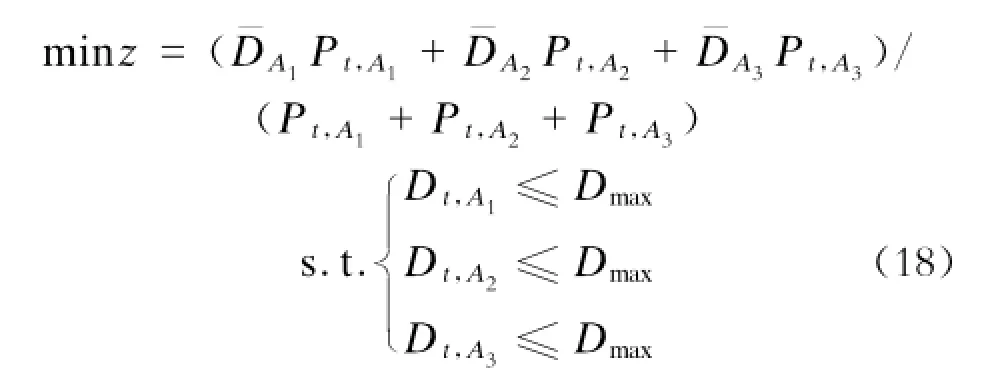
本文将岛式站台分为上行乘客候车区和下行乘客候车区，这2个区域共用相同的售票和进站闸机设施。当只有一个候车区（如上行候车区）出现乘客滞留时：

如果2个候车区域都出现乘客滞留，则应综合考虑乘客排队购票区、排队检票区、上行站台候车区和下行站台候车区共4个空间的乘客平均密度的加权算术平均值最小为目标函数：

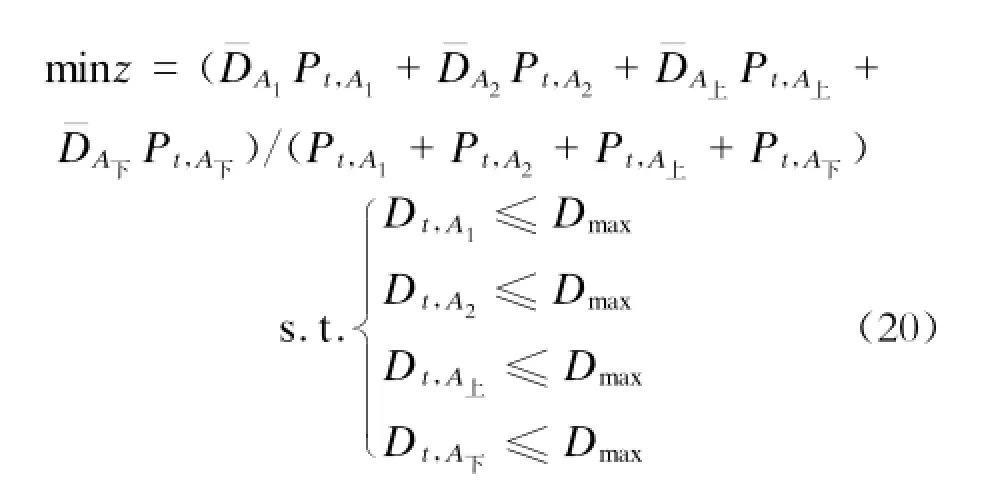
本论文建立的模型（式18～20）是1个非线性整数规划模型（售票设施数目和闸机数目均为整数），一般求解非常困难。但仔细分析不难发现，目标函数（式15～17）是关于变量（售票设施开放数目、闸机开放时数）的凸函数，而且所有的约束条件表达式也是关于决策变量的凸函数。因此，本论文建立的模型是一个凸规划，而且模型中的整数变量较少，只有2个，且取值范围也不大。所以，可以采用分枝定界的方法来求解，本文采用LINGO软件来进行求解。

2 实例验证

上海轨道交通1号线上海火车站站是一个重要的枢纽中转站，客流量大，特别是节假日期间，经常出现乘客滞留在站内的情况。

为防止密集客流对站点安全造成冲击，本文作者对1号线上海火车站站的空间、服务设施数目、服务设施服务能力等参数进行了调查，然后应用本文建立的模型来做实例验证。

2.1 调查结果

购票区的自助售票机总数为28台，人工售票窗口总数为15个。购票区的总有效排队服务面积A1=220 m2，平均每个人工售票窗口的服务能力C人=6人/min，平均每个自助售票机的服务能力C机=4人/min。

排队检票区的进站闸机（三辊闸机）总数为23台。排队检票区的总有效面积A2=100 m2。平均每个进站闸机的服务能力CZ=21人/min。

1号线上海火车站站的站台为岛式站台，站台上下行乘客有效候车区（即车门附近可以有效利用的排队区域）的面积A上=A下=180 m2。

设大型活动期间，出现下列客流状态：购票区乘客到达流率V1=200人/min，持有一卡通的乘客到达率V充=150人/min，购票区初始滞留乘客P0，A1=30人，检票区初始滞留乘客数P0，A2=40人，站台上行候车区初始滞留乘客P0，A3=50人，站台下行

候车区初始滞留乘客P0，A4=100人，列车到达间隔时间t=3 min，上行候车区α=0.2。

为了防止乘客过度拥挤，特别是候车站台的过度拥挤，本文取D级服务水平［8］为目标，平均密度上限Dmax=2.4 m2/人，即人均占用空间的下限为0.42 m2/人。

2.2 建立数学模型并求解

建立数学模型后，应用LINGO软件求解，得到如下计算结果：

在列车到达间隔3 min内，人工售票窗口开放的个数n人=4个，自动售票机开放的个数n机=12个，闸机开放的总时数n2=19 min。

文献［8］提出了行人排队等候区域服务水平的标准（见表1）。根据表1，对本实例优化计算结果如表2。

表1 排队区行人服务水平等级划分［8］

表2 实例优化计算结果

由表2可知，优化后各个区域的客流得到均匀的分布。需要说明的是，优化组织可以有多种组合，例如n人=8个，n机=4个。

如果按照常规管理模式，为了适应大流量客流，把所有的售票窗口、售票机、进站闸机开放，则站台下行候车区的列车到达时的最大密度为6人/m2，最小人均空间为0.16 m2/人，这就非常拥挤，容易发生挤伤、挤下站台或者踩踏等事故。其平均密度为3人/m2，平均人均空间为0.28 m2/人，处于E级服务水平，乘客很不舒服。

3 结语

本文利用系统工程的思想，针对客流超过车站正常客运设施所能承担的客流量的情况，考虑如何有效地调节客流服务设施的工作数量（如自动售票机、闸机等）以达到避免客流在某一排队区过度集中的目的，可以有效地避免过度拥挤而可能产生的安全风险。所建立的模型不仅可以用于指导实际的客流组织工作，可以计算车站的客流承受能力，还可以为车站的智能化控制提供理论基础。

［1］ 杨琳.地铁车站大客流组织模式研究［J］.高校理科研究，2009（9）：122.

［2］ 代宝乾，汪形，陈娅.北京地铁大客流安全问题分析及对策研究［C］∥中国职业安全健康协会.中国职业安全健康协会2009年学术年会论文集.北京：煤炭工业出版社，2009：223.

［3］ 葛世平.从大客流运营角度谈地铁车站的建筑布置优化设计［J］.百家论坛，2010（4）：1.

［4］ 费安萍.大客流地铁运营组织［J］.现代城市轨道交通，2005（2）：33.

［5］ 骆海瑛.地铁车站假日大客流的组织［J］.交通企业管理，2001（9）：11.

［6］ 符浩.地铁车站瞬间大客流客运组织模式研究［J］.交通企业管理，2010（6）：46.

［7］ 史小俊.地铁车站应对大客流的组织措施［J］.城市轨道交通研究，2009（10）：70.

［8］ Transportation Research Board.Highway Capacity Manual［M］.Washington D.C.，USA：National Resaerch Council，2000.

Optimum Facilities Collocation Model for Subway Stationin Condition of Large Passenger Flow

Zhang Yanni，Zhang Peng，Chen Hong，Bao Lixia

An optimum facilities collocation modelis established，with an object of the minimum average density of passengers（the maximum of average space occupied by passengers）for subway in case of large passenger flow.This model is formulated as an integer-nonlinear-problem，the integer variables are the numbers of opening ticketing facilities and gates.Based on Shanghai Railway Station of metro Line 1，this model is tested.The result shows when large passenger flow comes，this model could make an even distribution of passengersin variousspatial regions of the railway hub compared to the existing organizational methods，thus the service level can be significantly improved.

subway；large passenger flow；station facilities；optimization of collocation

U 291.6+3：U 231.4

2013-04-10）

*国家自然科学基金项目（51208232）；江苏省高校自然科学研究面上项目（13KJB580003）