地铁多区间钢轨电位分布及钢轨电位限制装置的合理投切

张栋梁 裴文龙 穆明亮

（中国矿业大学信息与电气工程学院，221008，徐州∥第一作者，副教授）

地铁多区间钢轨电位分布及钢轨电位限制装置的合理投切

张栋梁 裴文龙 穆明亮

（中国矿业大学信息与电气工程学院，221008，徐州∥第一作者，副教授）

目前地铁的钢轨电位分析大都是基于单侧供电或者双侧供电的单区间。实际上，钢轨电位分布受本区间供电影响较大，但也不能忽略相邻区间对其影响。使用MATLAB软件进行多区间钢轨电位仿真分析，并且根据仿真分析结果来实现钢轨电位限制装置的合理投切。

地铁；钢轨电位；电位限制装置

First-author'saddressSchool of Information and Electrical Engineering，China University of Mining and Technology，221008，Xuzhou，China

钢轨作为牵引电流回流系统的通路，是由多节钢轨通过无缝焊接而组成的。由于钢轨无法对地完全绝缘，轨地之间存在电阻，所以当牵引电流流经钢轨时，会有一部分电流泄漏到大地中，钢轨和大地之间就会存在轨地电位。地铁车辆和钢轨是等电位的，当乘客上下车时，就可能会横跨轨地而生产电压。为了保证人身安全，就需要在车站设置钢轨电位限制装置（OVPD），当轨地电位异常升高时，OVPD投入，将钢轨与地直接相连，降低轨地电位。此时，会有大量电流通过OVPD直接进入大地，造成杂散电流增大［1］。

本文以地铁多个供电区间为对象，以MATLAB软件仿真分析多区间钢轨电位分布，并通过几个相邻区间的钢轨电位来分析是否每个区间的OVPD都需要投入，从而实现OVPD更合理的投切。

1 模型的建立及计算

1.1 地铁牵引供电系统

地铁牵引供电系统结构如图1所示［2］。从图1中可知，每个变电站都与接触网相连，当列车运行时，给列车供电的不止是本区间的变电站，相邻区间的变电站也会提供；距离列车越远的变电站，供电越少。本文的以下分析均以4个区间为例进行。

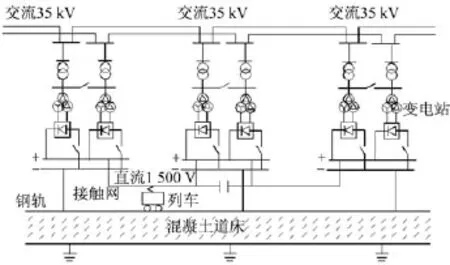
图1 地铁牵引供电系统结构示意图

1.2 多区间牵引电流的回流系统模型

对于地铁系统来说，可以认为轨道是一个纯阻性集中参数线，轨道与地之间只有纯阻性的电气联系，表征为过渡电阻，其单位为Ω·km；而轨道下面的大地也可以认为是一个纯阻性的参数线。所以，可将地铁牵引电流的回流系统分成一些有限单元。根据距离，可以推算出每一个有限单元的钢轨纵向电阻、轨地过渡电阻、大地电阻。然后，可用这些集

中参数来表示回流系统的分布参数，而其电流电压特性是一致的［3］。电流源可以代替列车向轨道注入的电流，或者代替列车紧急刹车时吸收的电流。通过这种方法构造出一个由集中参数组成的网络，如图2所示。

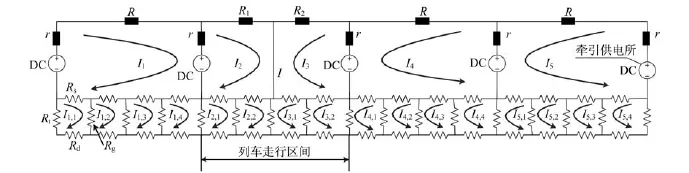
图2 地铁多区间牵引电流回流系统的离散模型

在图1中共有4个区间，每个区间分成4个有限单元。其牵引供电所的电压为DC 1 500 V；列车电流I为1 000 A；r为变电所等效电阻；R为牵引电网电阻；Rs为轨道纵向电阻；Rg为轨地过渡电阻；Rd为大地纵向电阻；Rt为变电所接地电阻［4］；I1～I5为牵引区各网孔的电流值；I1，1～I5，4为有限单元各网孔的电流值。

从图2模型可通过网孔电流法，得到各个有限元的电流表达式如下：

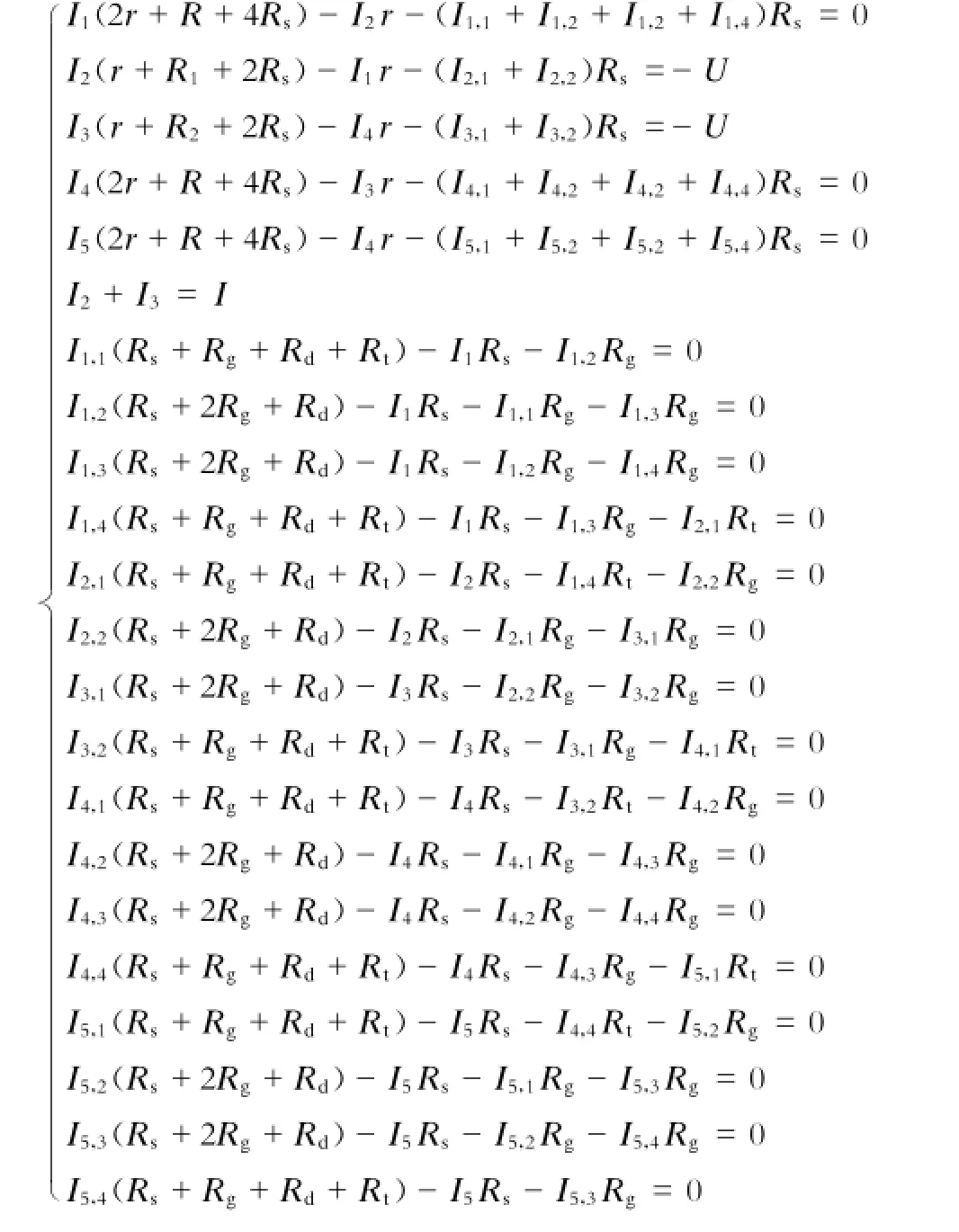
当然，有限元的划分可以随意设置，划分得越多，离散模型越接近连续模型，但运算量越大。网孔电流方程很多，电流参数较多，可以通过列注法得到各个电流，然后根据电流差得到泄漏电流，再根据欧姆定律可得钢轨对地电压，当然也能得到杂散电流的大小。具体算法如下：

则泄露电流

钢轨电位

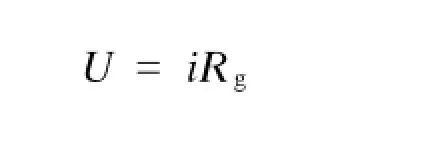
2 仿真图形

根据上述模型与计算，只要代入钢轨及大地的具体参数即可得到多区间钢轨电位分布。钢轨及大地的具体参数如下：供电区间长度L=1.2 km；牵引供电所的电压U牵=1 500 V；I=1 000 A；r= 0.022 4Ω；R=0.008Ω/km；Rs=0.026Ω/km；Rg=15Ω·km；Rd=0.01Ω/km；Rt=0.5Ω。

根据上述参数在MATLAB软件中进行两个仿真。图3为列车在第一个区间内运行时的钢轨电位分布图；图4为列车在第二个区间内运行时的钢轨电位分布图。由于这个模型是个纯电阻模型，所以列车在第三、第四个区间内的钢轨电位分布图与第二、第一区间的钢轨电位分布具有对称性，此处就不再仿真。

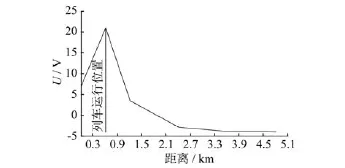
图3 列车在第一区间运行时钢轨电位分布图

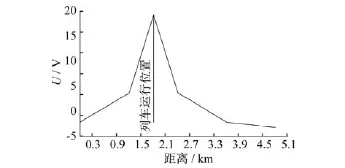
图4 列车在第二区间运行时钢轨电位分布图

由图3、图4可得以下结论：

1）在相同条件下，列车在不同位置时，其钢轨电位分布趋势基本相同，都是列车位置处钢轨电位最高，两侧逐渐降低，与单区间相同。

2）列车在不同位置时钢轨最高电位的大小不同。列车在第一区间时钢轨最高电位约为21 V，列车在第二区间时的钢轨最高电位约为18 V。在正常情况下，两者相差3 V；如果在车辆起动或者重载时，电压差可能会更大。也就是说，当列车行进在两侧的变电所时，钢轨电位比列车行进在中间变电所时更高。

3）变电所的负极电位不一定是负的。由单区间钢轨电位分析可知，列车位置处的钢轨电位为正的最大值，而变电所负极处为负的最大值；但由多区间模型分析可知，变电所负极的电位可能是正的。

4）变电所的负极电位与列车具体位置有关。当列车在第二区间时，与列车相邻的变电所负极的电位约为4 V；而当列车在第一区间时，与列车相邻的变电所负极的电位约为7 V与4 V。这就为钢轨电位限制装置的投切提供了相应的依据。

3 钢轨电位限制装置的投切

根据上述的分析可知，列车运行时，在车站或者变电所处的钢轨电位可能是正的。如果在列车起动时牵引电流增大，或者出现绝缘损坏等种种原因导致钢轨电位异常升高而达到影响人身安全时，钢轨电位限制装置就需要投入。钢轨电位限制装置投入后，钢轨与地直接相连，电位被钳制到零。但此时大量电流通过OVPD流入大地，会导致杂散电流增大，使钢轨附近的埋地金属管线、钢筋结构及地铁设备等产生严重腐蚀。这是一个矛盾的问题，所以需要对OVPD进行合理地投切。

实际上，钢轨电位的异常升高可能会达到90 V甚至更高。以下所做的钢轨电位异常升高的仿真虽然未达到90 V，但分析结论是相同的。

图5、图6的地铁牵引电流取3 000 A，以仿真钢轨电位的异常升高情况。图5为列车在第一区间运行时的钢轨电位分布，以及前后变电所OVPD投入后的钢轨电位分布；图6为列车在第二区间运行时的钢轨电位分布，以及前后变电所OVPD投入后的钢轨电位分布。

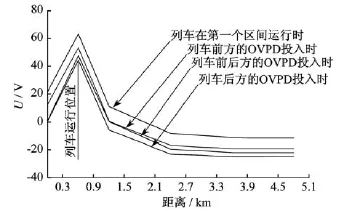
图5 列车在第一区间运行时及OVPD投入后的钢轨电位分布

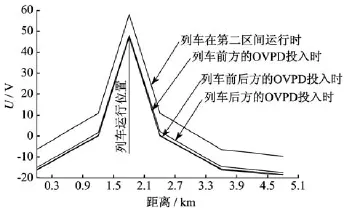
图6 列车在第二区间运行时及OVPD投入后的钢轨电位分布

如图5所示，列车在第一区间运行时，后方变电所处的钢轨电位约为20 V，前方变电所处的钢轨电位约为10 V。当前方变电所的OVPD投入时，使

整条线的钢轨电位下降，但是列车后方的变电所处的钢轨电位还是大于零，而且不能确定它是否超过危险电位；当列车前后变电所的OVPD都投入，使4个区间钢轨的电位都下降，且列车前后变电所的电位都钳制到零，完全可以保证人身安全。但是列车前后2个OVPD投入后，会有大量电流经过OVPD流入大地，导致杂散电流增大，使周围金属的腐蚀增大。当列车后方的OVPD投入时，整条线的钢轨电位下降，且列车前方的变电所处钢轨的电位还是低于后方变电所处钢轨的电位，可以保证列车前方的安全；而此时只有1个OVPD投入，比2个OVPD投入时的泄漏电流小。

如图6所示，列车在第二区间运行时，列车前后方变电所处的钢轨电位基本相等，无论投入后方、前方还是前后方的OVPD，都可以保证整条线路的安全。但是，单方向OVPD投入时的泄漏电流比双方向OVPD投入时的泄漏电流要小得多。

根据以上分析可知，当列车前后方变电所处钢轨电位都超过OVPD的合闸要求时，可只将电位较高变电所的OVPD投入即可。这样既可保证整条线路钢轨的电位达到安全值，又可防止由于过多OVPD投入而导致杂散电流过大的危害。

4 结语

本文对多个区间钢轨进行有限元分解，得到地铁牵引电流回流系统的离散模型；再根据网孔电流法，计算出多区间钢轨电位的分布；最后通过数学模型对不同位置OVPD投入时的钢轨电位进行仿真，得到了一种OVPD更为合理的投切方式。当然，此时的OVPD不仅需要对轨地电压进行实时监测，相邻的OVPD也要进行实时通信，以防2个相邻的OVPD同时接地，造成杂散电流的大量泄漏。

［1］ 王禹桥，李威，杨雪锋，等.对地铁轨道电位异常升高的研究［J］.城市轨道交通研究，2009（8）：35.

［2］ 张健根.广州地铁供电系统33 k V环网接线方式的思考［J］.城市轨道交通研究，2006（7）：1.

［3］ 李国欣.直流牵引回流系统分析及轨电位相关问题研究［D］.徐州：中国矿业大学，2010.

［4］ 张少强.城市轨道交通钢轨电位研究与抑制［D］.徐州：中国矿业大学，2012.

式中：

J——车轮与轮座之间的过盈量，mm；

d1——轮座直径，mm；

d2——与之配合的车轴轮毂孔直径，mm。

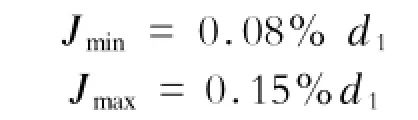
车轮压装过盈量J须满足下列要求：

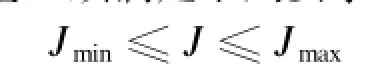
即：

在计算机程序中，设置了压装过盈量超出阈值报警装置，当超差时自动报警，同时锁定压装机压装程序，自动拒绝压装。

制动盘压装过盈量的超差报警装置设计，其不同点只是在于将不同型号的制动盘过盈量输入，其它与车轮压装基本相同，不再赘述。

4 结语

轮对是车辆转向架的重要部件，其质量状况直接关系到铁路运营安全。尽管本自动判断程序研究成果是完全按照TB/T 1718—2003中的各项规定进行数字化处理，以实现机器智能自动判断功能，但因其产品的重要性，在生产实践中，对机器判断合格的压装力曲线，还必须由操作者、工长、检查员、验收员分别对压装力曲线进行人工判断，以杜绝自动判断程序可能发生的误判现象。只有当机器和人工判断均合格时方可判定为合格品，以期最大限度保障旅客列车的行车安全。实践表明，按照本文研究的数学模型编制的压装力曲线自动判断程序生产的产品，通过人工判断验证后的正确率接近100%。本成果为完善相关铁路标准，优化自动判断程序提供了借鉴。

参考文献

［1］ 周兰英.轮对压装曲线不合格的原因及对策［J］.铁道机车车辆工人，2001（1）：2.

［2］ 王勋龙，隋振.轮对压装过程监控系统设计［J］.机床与液压，2011（6）：61.

［3］ 袁旭芳.铁路车辆轮对压装曲线陡跳工艺探讨［J］.煤矿机械，2005（5）：91.

［4］ TB/T 1718—2003铁道车辆轮对组装技术条件［S］.

［5］ 张元涛，张顺启.关于轮对压装工艺参数优化设计的探讨［J］.铁道车辆，2006（7）：29.

（收稿日期：2013-01-17）

Rational Distribution of Rail Potential and OVPD's Switch in Multiple Metro Intervals

Zhang Dongliang，Pei Wenlong，Mu Mingliang

At present，metro rail potential analysis is basi- cally related to unilateral or bilateral power supply single interval，but in reality，the distribution of rail potential is largely influenced by the interval power supply，the impact of adjacent intervals can not be ignored at the same time.In this paper，a modeling analysis of multiple intervals is conducted by using MATLABsoftware，and the result is used to achieve a reational distribution of OVPD switching.

metro；rail potential；over voltage protection device（OVPD）

U 284.24

2013-10-12）