混沌时间序列预测算法的优度评价

王 䶮，盖明久，张金春

（海军航空工程学院a.研究生管理大队；b.基础部，山东烟台264001）

由于混沌时间序列具有非线性动力学特性，所以是长期不可预测的，但确定性结构又使系统演化轨迹短期内的发散较小，只满足短期可预测性。混沌时序预测就是在重构后的相空间中找到某种模型去最大程度地逼近系统的动力学特性，并用这个模型实现系统未来趋势的预测[1-2]。混沌时间序列预测方法可分为3类：全域预测[3]、局域预测[4]和自适应预测[5]。

在实际应用中，评价一个算法优劣的指标一般包括可预测步数与算法速度。目前，在评价一个算法的性能时，只是将以上2个指标单独的进行比较，不能全面地衡量算法的优劣。

优度评价方法是可拓学[6-8]中评价一个对象（事物、策略、方法等）优劣的基本方法，能够在合适的评价指标体系下，对待评对象进行综合评价，确定其综合优度值。本文采用优度评价法对混沌时间序列的4种局域预测算法进行评价，获得了较好的效果。

1 混沌时间序列的局域预测算法

对混沌时间序列进行预测，首先要对混沌时间序列进行相空间重构。根据相空间重构方法，混沌时间序列{x (t),t=1,2,…,N} 在延迟时间τ、嵌入维数m 条件下重构后共有M个相点，M=N-(m-1) τ，各个相点依次是：

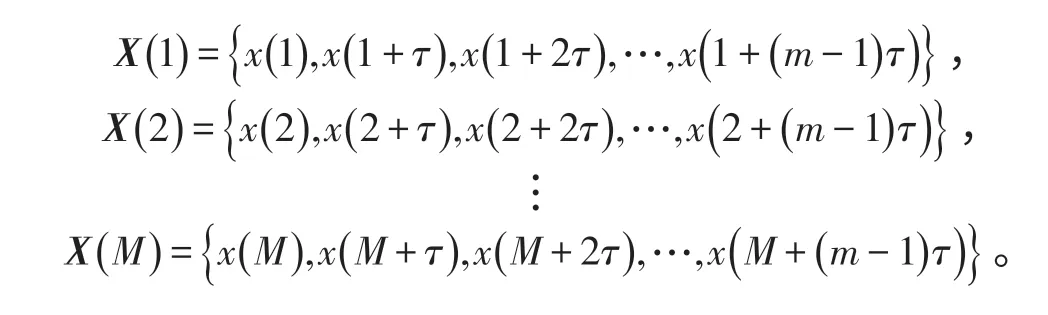
相点X(M)进一步演化后的相点为

因此，如果知道X(M+1)，可用其最后一维元素x(M+1+(m-1) τ)来预测序列的下一点X(N+1)。

混沌时间序列的局域预测算法不对所有相点进行拟合，只研究部分邻近相点，认为某一相点的未来演化趋势与其邻近相点的演化行为类似。由于拟合的相点数量少，因而在拟合方面具有计算复杂度低、速度快、拟合度高、适用于多数系统的优点，而且，由于拟合的相点少，并且是变化的，具有很强的适应性，更符合混沌时间序列的变化性质。因此，局域预测法得到了广泛的研究和应用。常用的局域预测法有以下4种[9]。

1.1 局域平均预测法

局域平均法认为最后一个相点X(M)进一步演化行为可由它的若干个邻近点的平均进一步演化行为来估计，因而先按一定的规则找出X(M)的k个邻近点X(Mi)(i=1,2,…,k)，即由推出其中，表示序列下一点x(N+1)的预测值。该方法直观易懂，计算简单，但易受噪声干扰。

1.2 加权零阶局域预测法

为了更准确地预测变化较大和含有噪声的序列，加权零阶局域预测法，对各个邻近相点依据特定的规则赋予权重。其具体公式如下：

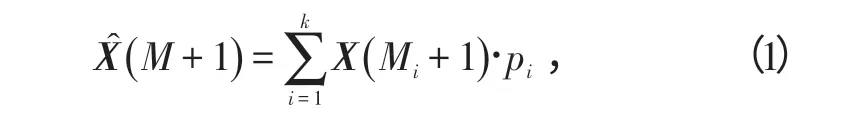
式中，pi(i=1,2,…,k)是权值。

1.3 加权一阶局域预测法

加权一阶局域预测法是用一阶线性拟合的方式来逼近相点的演化趋势，公式为

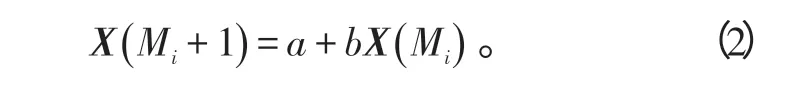
将每个相点分解为各维分量，则有：

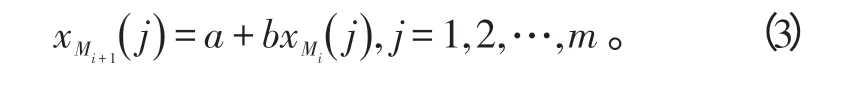
使用加权最小二乘法来求取最佳的a 和b值，从而得到相点演化的预测公式，得到下一步演化相点的预测，提取最后一维分量即为时间序列的预测值。

1.4 基于SVM的局域预测法

基于SVM的局域预测法具有很好的泛化能力，并能克服维数灾问题及局部极小问题。选用sigmoid核函数进行预测[10]，公式为

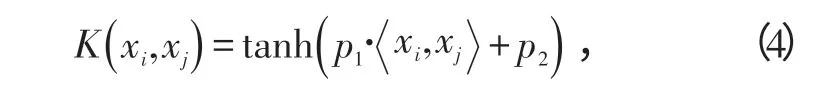
式中，p1、p2是2个待定参数。

基于SVM的局域预测法的基本思路为：首先，计算原始时间序列的延迟时间τ 和嵌入维数m，完成相空间重构，选定合适的邻近相点个数K。将以上得出的邻近相点集合作为支持向量机的训练集输入，将其下一步演化点的最后一维元素所组成的集合作为训练集输出，设置支持向量机核参数p1、p2进行训练。然后，将预测中心相点作为测试集输入到训练好的支持向量机中，得到输出，即为预测值。由此，预测值便能重构得到新的预测中心点，同时将预测值作为已知序列点加入到原样本集中，形成新样本集。重复这一思路，直到完成所有预测。

2 混沌时间序列预测算法的优度评价方法

混沌时间序列预测的优度评价流程如图1所示。

图1 混沌时间序列预测算法优度评价流程图Fig.1 Flow chart of priority degree evaluation of chaotic time series prediction algorithm

2.1 评价指标的选取

对一个混沌时间序列预测算法一般从算法的精度和运算速度来进行评价。评价预测算法的精度有多种指标，一般采用平均绝对百分误差（Mean Absolute Percentage Error，MAPE）来衡量，公式如下：

式（5）中：S为预测步数；y(t)为真实值；y′(t)为预测值。

但是，平均绝对百分误差会将误差“平摊”，在某些意义上有失客观的缺点，因而本文使用一个新的衡量预测算法性能的指标：单点预测准确率与平均绝对百分误差来综合评价算法的精度。

单点预测准确率的公式如下：

另外，在序列预测中，预测速度也是一项非常重要的指标，直接决定该预测算法是否具有实用价值，我们希望预测算法越快越好，最好能实现实时或近似实时的预测。特别对于实际应用问题，如果预测算法耗时过长，往往失去应用价值。因此，不同算法对混沌时间序列的预测时间也应作为评价的指标之一。具体混沌时间序列预测算法评价体系如图2所示。

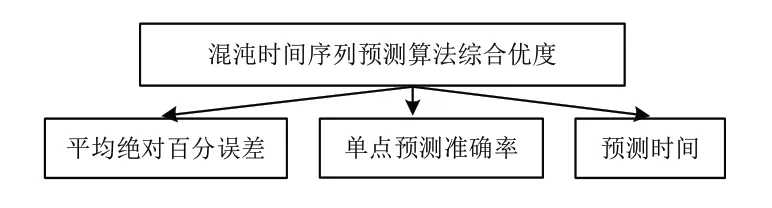
图2 混沌时间序列预测算法评价体系Fig.2 Evaluation system of chaotic time series prediction algorithm

2.2 确定各评价指标的权系数

对待评价算法Zj(j=1,2,…,m)各指标的重要程度进行评估，以权系数表示各评价指标的重要程度。在实际混沌时间预测时进行多步预测。因此，将待评价算法的平均绝对百分误差、单点预测准确率和预测时间看作第1层评价指标，各指标对应的不同预测步数的值看作第2层评价指标。以SI1,SI2,…,SIn为第1层系统的评价指标，SI11,SI12,…,SI1p1；SI21,SI22,…,SI2p2；…；SIn1,SIn2,…,SInpn为各个第1层系统对应的第2层系统的评价指标[9-11]。然后，根据经验、专家打分法或层次分析法等分别对各级指标赋予[0,1]的值。一级系统权系数记为α=(α1,α2,…,αn)，二级系统权系数记为：β1=(β11,β12,…,β1p1)，β2=(β21,β22,…,β2p2),…，βn=(βn1,βn2,…,βnpn)，其中，i=1,2,…,n。

在确定各级各个指标的权重之后需要先计算二级系统的优度值，然后乘以对应一级系统的权重得出对象的最终优度值。

2.3 建立关联函数，计算关联度

在仿真所得数据的基础上，对所确定的指标集中的指标v 建立关联函数Kv(x)。其正域为X=(a,b)，当x=a时，算法的精度最高或者速度最快，即量值越小算法的精度或者优度越大。建立关联函数为：

临界值a、b可通过多次的仿真实验和专家的意见来确定。

把待评价算法Zl关于各二级评价指标SIij的量值代入关联函数式（7）中，求出关联函数值，简记为klij，则各评价对象Z1,Z2,…,Zm关于SIij的关联度为：

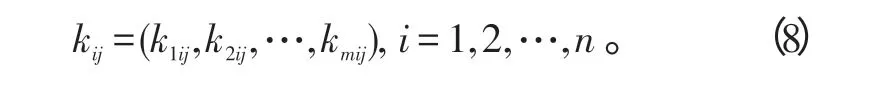
2.4 计算各评价算法的优度值

待评价算法Zl(l=1,2,…,m)关于各一级评价指标下的二级指标SI11,SI12,…,SI1p1，SI21,SI22,…,SI2p2，…，SIn1,SIn2,…,SInpn的关 联 度 分 别为：k1(Zl)=(kl11,kl12,…,kl1p1)T，k2(Zl)=(kl21,kl22,…,kl2p2)T，…，kn(Zl)=(kln1,kln2,…,klnpn)T，则待评价算法的优度值为：

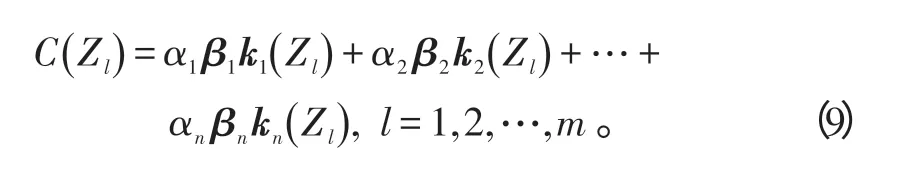
3 对4种混沌时间序列的局域预测算法的优度评价

以Lorenz 混沌时间序列为例子。设置参数a=16，b=4，c=45.92，初值 x(0)=-1y(0)=0，z(0)=1，积分区间[0,1 000]，积分时间步长0.01。用四阶Runge-Kutta 法求解方程组，并以x分量的第10 001个到第13 000个总计3 000个数据点为样本。首先，用相空间重构方法计算该样本的延迟时间和嵌入维数，得到τ=11和m=6，以此参数组合进行重构；然后，以第1节中的4种不同局域预测算法分别进行10步、50步、100步的预测，得到的结果及各指标的权值如表1所示。局域平均法、加权零阶法、加权一阶法和基于SVM法分别用Z1、Z2、Z3、Z4表示。

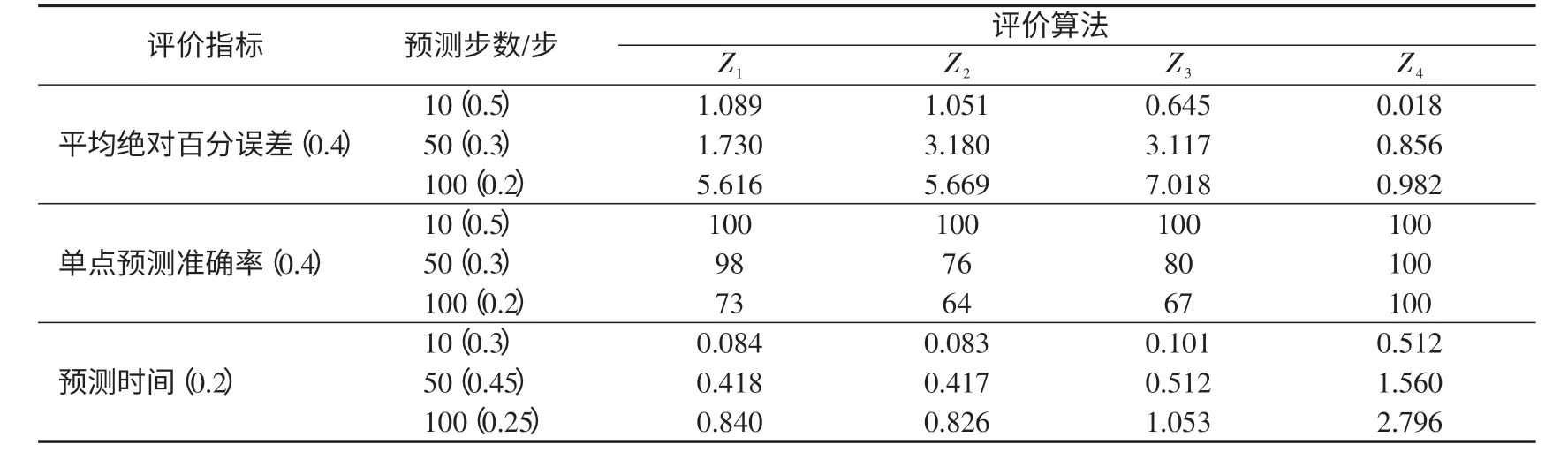
表1 4种算法的仿真结果及各评价指标权值Tab.1 Simulation results of four algorithmsand evaluation index weight %

表1中“（）”内的值为各评价指标与预测步数的权值。把Z1、Z2、Z3、Z4关于评价指标的量值代入关联函数，求出对应于式（8）的关联度，分别为：

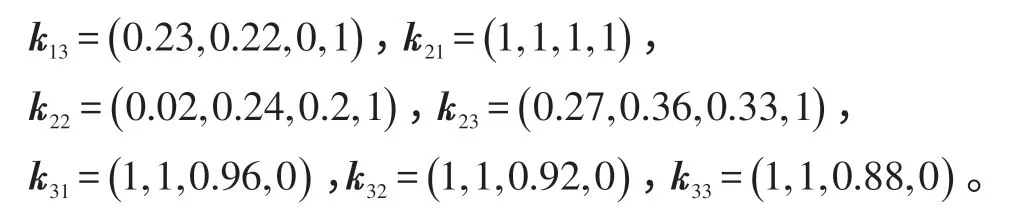
计算出待评价算法的综合优度值，结果见表2。

表2 4种算法的优度值Tab.2 Priority of four algorithms

4 结束语

利用优度评价方法对混沌时间序列预测算法进行评价，可以综合算法的精度和速度两方面评价算法的优劣。实例证明：优度评价方法实用性较高，可以有效评价算法综合性能的高低，而且解算方便，为混沌时间序列预测算法的评价提供了一种定量化的方法和思路。

[1]高俊杰，王豪.基于改进的G-P算法的相空间嵌入维数选择[J].计算机工程与应用，2012，35（12）：1-5.

GAO JUNJIE，WANG HAO.Determination of embedding dimension for phase space based on improved G-P method[J].Computer Engineering and Applications，2012，35（12）：1-5.（in Chinese）

[2]高俊杰，王豪.基于支持向量机的混沌时序局域预测[J].计算机仿真，2013，30（11）：303-306.

GAO JUNJIE，WANG HAO.Chaotic time series local prediction based on SVM[J].Computer Emulation，2013，30（11）：303-306.（in Chinese）

[3]吕金虎，陆君安，陈士华.混沌时间序列分析及其应用[M].武汉：武汉大学出版社，2002：94-98.

LV JINHU，LU JUNAN，CHEN SHIHUA.Chaotic time series analysis and application[M].Wuhan：Wuhan University Press，2002：94-98.（in Chinese）

[4]Farmer J D，Sidorowich J J.Predicting chaotic time series[J].Physical Review Letters，1987，59（8）：845-848.

[5]甘建超，肖先赐.基于相空间邻域的混沌时间序列自适应预测滤波器（I）线性自适应滤波[J].物理学报，2003，52（5）：1096-1101.

GAN JIANCHAO，XIAO XIANCI.Adaptive predict-filter of chaotic time series constructed Based on the neighbourhood in the reconstructed phase space（I）linear adaptive filter[J].Acta Physica Sinica，2003，52（5）：1096-1101.（in Chinese）

[6]杨春燕，蔡文.可拓工程[M].北京：科学出版社，2007：70-170.

YANG CHUNYAN，CAI WEN.Extenics engineering[M].Beijing：Science Press，2007：70-170.（in Chinese）

[7]陈军生，周文明.基于可拓方法的装备保障动态评估模型[J].四川兵工学报，2010，31（11）：1-4.

CHEN JUNSHENG，ZHOU WENMING.Dynamic assessment model of equipment supp-ort based on extenics method[J].Sichuan Ordnance Journal，2010，31（11）：1-4.（in Chinese）

[8]蔡文，杨春燕，何斌.可拓逻辑初步[M].北京：科学出版社，2003：25-106.

CAI WEN，YANG CHUNYAN，HE BIN.Extension logic[M].Beijing：Science Press，2003：25-106.（in Chinese）

[9]韩敏.混沌时间序列预测理论与方法[M].北京：中国水利水电出版社，2007：23-80.

HAN MIN.Prediction theory and method of chaotic time series[M].Beijing：China Water Power Press，2007：23-80.（in Chinese）

[10]VAPNIK V.The nature of statistical learning theory[M].New York：Springer，1999：30-53.