基于最大阈值的改进EZW图像压缩技术研究

李万社， 张洪涛， 房小蒙

(陕西师范大学 数学与信息科学学院， 陕西 西安 710062)

0 引 言

图像压缩编码是信息技术领域研究中最活跃的课题之一。由于小波变换具有许多其它时(空)频域分析方法所不具备的优良特性，更适合于图像数据的处理[1]。随着科学研究的发展，出现了多种新的编码方法，比如分形编码[2]、SPIHT分层树集合分裂编码[3-4]等。其中基于小波变换的EZW的编码方法已被公认为处理图像压缩技术的最好方法之一。但是在实际操作过程中，由于传统的EZW方法需要对不同子带进行重复扫描，因此势必造成冗余编码，也会加大运算量和运算时间，需要做进一步的研究改进。

本文将小波变换与位平面编码结合，首先介绍了传统EZW(embedded coding using zero-trees of wavelet coefficients，零树嵌入式算法)的基本原理，在此基础上，引入了基于EZW图像压缩编码的改进方案，同时用MATLAB 6.5对方案进行了相应的实验，并对去高频算法、传统EZW和本文算法3种编码的实验结果进行了对比和分析。

1 EZW编码

1.1 EZW算法简介

EZW是Shapiro于1993年将零树数据结构和比特平面编码技术结合起来而提出的[5]。它采用“零树”结构的形式进行扫描，充分利用了不同尺度间小波系数的相似特征，考虑用很少的压缩位对大量的零进行编码，有效地剔除了针对高频小波系数的编码，极大地提高了小波系数的编码效率。

1.2 EZW算法思想

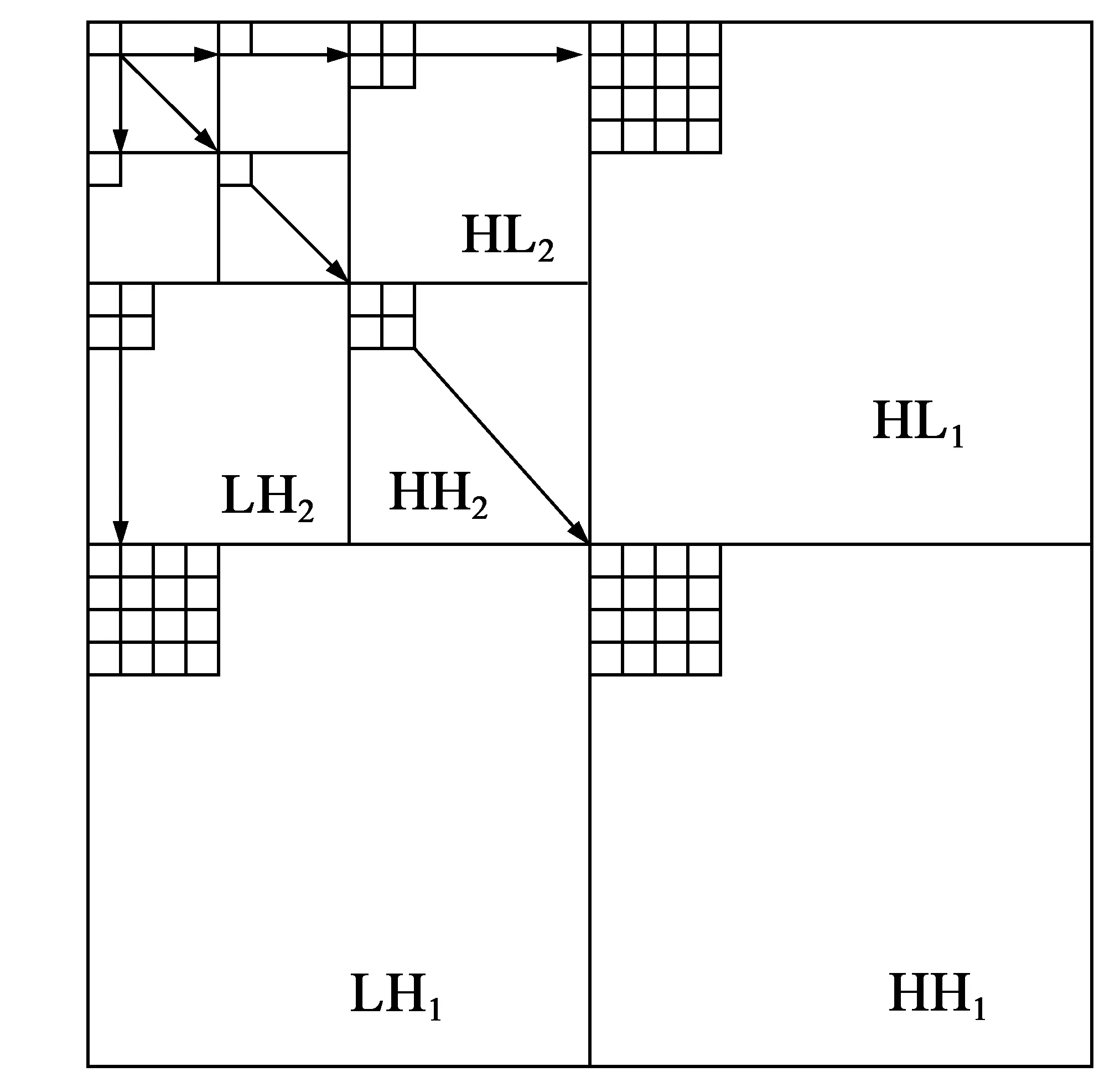
图1 三级小波变换的 空间频率树结构

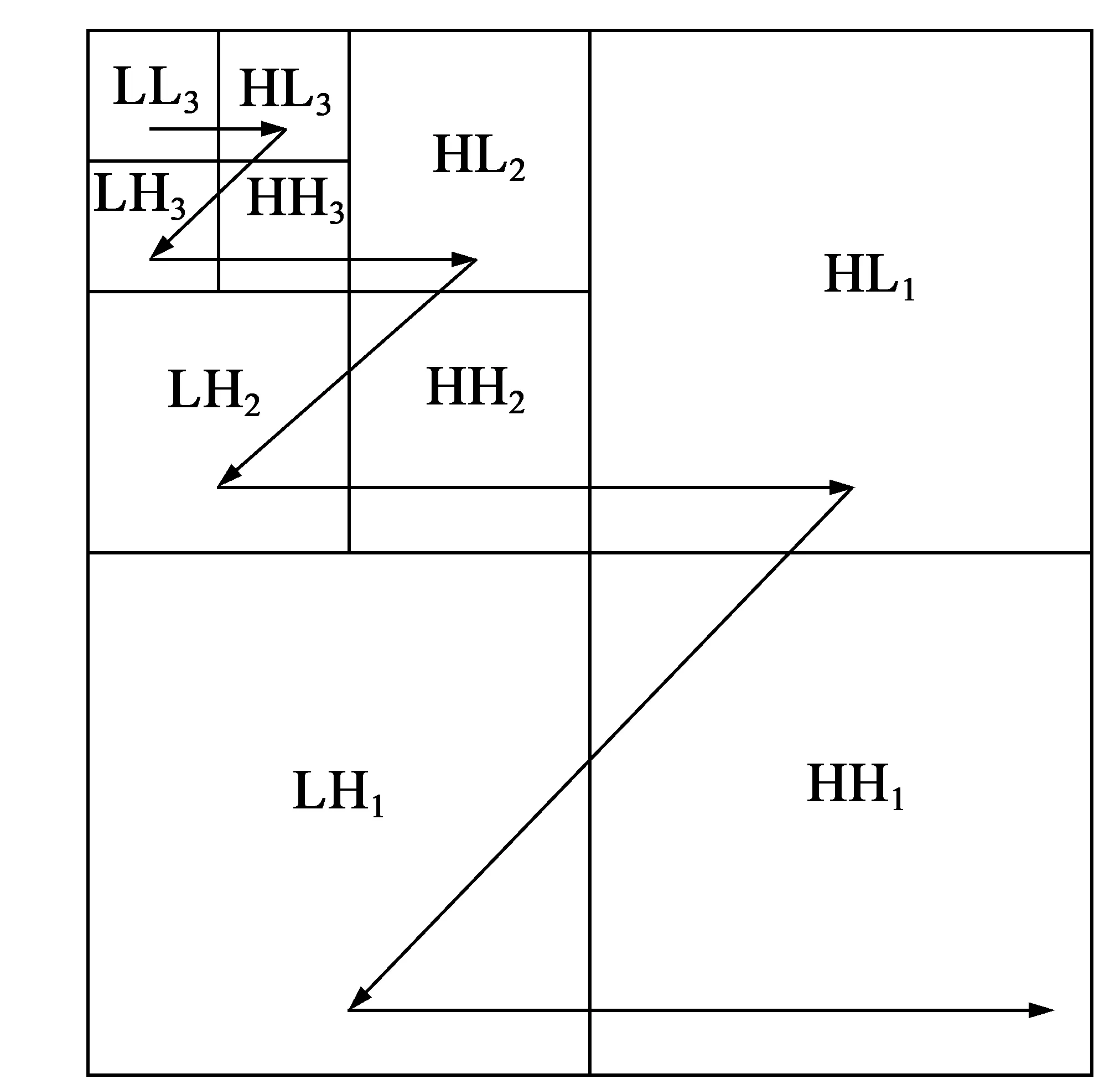
图2 具有三级尺度的小 波变换系数的扫描顺序图

EZW算法采用零树量化方法，基本思想是：在量化小波系数时采用了零树(zero-trees)这种数据结构。

图1是通过三级小波变换而形成的深度为4的树。一幅经过小波变换的图像按其频带从低到高形成一个树状结构，树根是最低频子带的结点，它有3个孩子分别位于3个次低频子带的相应位置，其余子带(最低频子带除外)的结点都有4个孩子位于高一级子带的相应位置(由于高频子带分辨率增加，所以一个低频子带结点对应有4个高频子带结点，2×2矩阵)。

EZW算法使用了4个符号进行编码：零树根(ZTR)、孤立零(IZ)、正显著(POS)和负显著(NEG)[5]。扫描中访问到的每一个系数都被分类到上述4个符号中。每次迭代都按照图2所示的“Z”形图顺序扫描全部系数。这可以保证当访问一个节点时，它的所有父节点都己经扫描过了。扫描从最低频率子带LLn开始，依次扫描HLn,LHn,HHn，然后来到第n-1层，再扫描HLn-1,LHn-1,HHn-1。在算法进行到下一个子带之前，对每个子带都进行了充分的扫描。

2 改进EZW算法(最大阈值算法)

2.1 最大阈值组

由于传统EZW算法中要求多次扫描，因此会将阈值减半依次迭代，无疑加大了重复运算量。由小波变换多分辨理论得知，图像经过N级小波分解后，可以得到3N+1个子带。假设第k个子带Dk(k=1,2,…,3N+1)中绝对值最大的小波系数为tk，则最大阈值组A定义为A={|tk|;k=1,2,…,3N+1}。|t3k-2|,|t3k-1|,|t3k|分别表示HHk,LHk和HLk中的最大阈值，例如|t6|表示HL2中的最大阈值(图2)。这样通过最大阈值组将子带分作不同区段，先完成整带扫描。

其次将初始阈值T0定义为：T0=2[log2C]，这里C为所有子带中小波系数的最大值，第i个阈值定义为：Ti=2-iT0，i为迭代次数。

通过这样设定的阈值，运算中可以在第i次迭代中只扫描|tk|>Ti的这部分子带(称为重要子带)，反之则不扫描(称为非重要子带)。

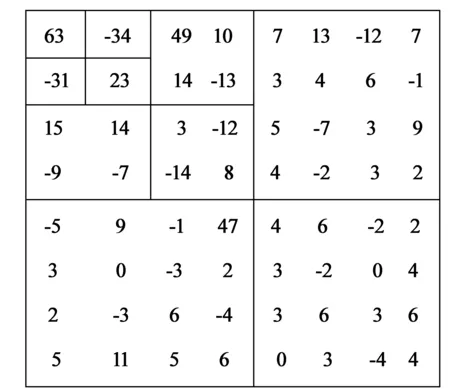
图3 8×8三层小波分解系数图

由图3我们可以得到各子带最大阈值及重要子带。例如|t7|表示HH3中的最大阈值，即：|t7|=23。这样当阈值为T=25时，|t7|<25，就可以跳过这一子带不扫描；当阈值减半为T=24时，就认为其是重要子带进行扫描。因此该方法可以整带扫描，不必重复扫描每个系数，做到不重不漏，不仅能够逐次逼近量化嵌入，提高运算精度，而且能大大节省运算时间。

2.2 算法过程

算法选取具有紧支撑、高正则性的双正交小波基Daubechies 9/7[6]小波。改进EZW具体实现时，首先进行对称的正交小波变换，然后判断是否为重要子带，接着对门限值重复做循环，在每次迭代后门限值都减半。门限用于计算显著和非显著小波系数的显著性图，并利用零树来表示。在EZW编/解码过程中，始终保持着主表和副表两个列表。主表包括编码中的不重要的集合和系数，输出信息起到了恢复各重要值的空间位置作用，而副表包括编码中的有效信息，输出为各重要系数的二进制值。主要步骤如下[7]：

a)初始化：初始阈值设定为T0=2[log2C]，此后每扫描一次，阈值减小一半；

b)判断子带：|tk|>Ti为重要子带，继续扫描，否则不扫描；

c)主扫描：按图4中所示的扫描次序，将小波系数与阈值Ti进行比较，若|c(i, j)|>Ti，则输出一个符号，用一个主扫描表记录这些输出符号；

d)辅扫描：对主扫描表进行顺序扫描，对其中输出符号为POS或NGE的小波系数进行细化，方法是将显著系数的二进制表示多送出1位，当解码器收到这一位后，给当前系数值增加±0.25Ti；

e)重新排序：为便于设置下一次扫描所用的量化间隔，以提高解码的精度，对输出符号为POS或NEG的数据重新排序；

f)输出编码信号：编码器输出两类信息，第一类是给编码器的信息，包括阈值、主扫描表和辅扫描表；第二类是用于下次扫描的信息，包括阈值及上步中重新排序过的重要系数序列；

g)如果主扫描表未消失，将阈值Ti降低一半，即令Ti+1=Ti/2，转到b)重新扫描。

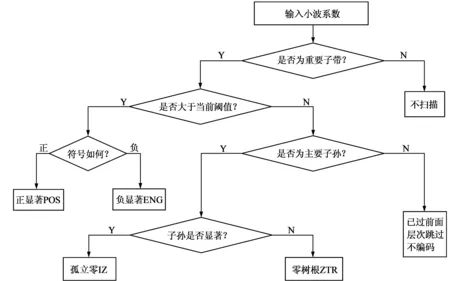
图4 改进EZW编码流程图

编码分为主通和副通两个过程。在主通过程中，在给定阈值下，按照图4所示的流程，对主表进行编码扫描。若为重要系数，则将其幅值加入副表中，然后将该系数在数组中置为零。在副通过程中，需对副表中的重要系数进行细化。

3 仿真实验

3.1 去除小波分解高频信息的压缩算法

首先采用去除小波分解后LH、HL、HH高频信息的压缩方法进行实验。其具体的算法步骤如下：

(1)对一幅图像来进行多层小波分解。

(2)保留最高层小波分解的水平垂直低频系数LLn，可以不需编码直接传输LLn。如果进行一层小波分解则信息量变为原来的1/4，二层小波分解信息量为原来1/16，…，N层小波分解信息量为原来的1/4N。当然也可以对LLn进行编码后传输。

(3)解压缩的时候，认为所有层的3个方向的高频系数全为0，对其进行补0后逆小波变换。

本文采用MATLAB 6.5编程进行了仿真实验，实验图像采用灰色图像Lenna，该图像有512×512个像素点，采用的小波为Daubechies 9/7小波，分别对该图像进行一层、二层、三层小波分解，并去除其高频，然后进行重构，计算其信噪比和均方误差，其结果如图5和表1所示。

(a) 原图像 (b) 一层分解重构图 (c) 三层分解重构图图5 去高频算法在不同分解层数下的重构图像

小波分解层数一层二层三层MSE4.65771.571180.12SNR/dB26.90714.90510.674

从实验结果可以看出：该算法在三层小波分解后数据量压缩为原来1/64，重构后效果较差，图像失真率很大，均方误差为180.12，信噪比为10.674。可见，这种去除图像高频信息仅保留低频信息的压缩方法，是一种最简单的压缩方法，并没有经过其它的处理，因此分解层数越多，压缩比越高，而图像失真率也越高。

3.2 EZW与改进EZW算法比对实验

零树小波编码需要将得到的比特流按其重要性进行排序。在实验中，采用与前面一样的原图像和小波滤波器。图6中(a)到(d)分别是在0.125，0.25，0.5，1.0倍比特率下经过改进EZW编码后恢复的图像。

(a) 0.125 bps (b) 0.25 bps (c) 0.5 bps (d) 1.0 bps图6 改进EZW算法在不同比特率下的图像

从图6中可以看出，经过改进EZW编码(下表记为MTEZW)后恢复的图像，比特率越高，虽然编码后的文件越大，但图像的质量越好。当比特率为0.125时，图像很模糊；当比特率为0.25时，图像比较模糊，只能属于中等质量；当比特率到0.5时，图像质量有所提高，但仍然能从人眼分辨出图像的失真；但当压缩比特率达到1.0的时候，从主观上已经达到了“无失真”的图像质量。实验数据见表2、表3。

表2 EZW与本文MTEZW算法在不同比特率下的峰值信噪比

表3 EZW与本文MTEZW算法编/解码(编码+解码)时间比照

通过以上实验结果的对比和分析，最大阈值EZW算法产生的压缩图像失真度低，图像平滑，有良好的视觉效应。另外，其运算用时及复杂性大大减少，实现了更高的编码效率。

4 结 语

本文对小波变换在图像压缩领域的应用做了初步探讨，主要介绍了基于最大阈值的EZW改进算法的原理、步骤，该算法简单且具有较好的压缩比。最后，使用MATLAB编程，并比较了与去除高频分量算法、传统EZW压缩算法的实验结果。表明改进的EZW效果更加显著。

[参考文献]

[1] RAFACEL C,RICHARD E.数字图像处理[M].阮秋琦,译.北京:电子工业出版社,2003:369-372.

[2] 景晓军,周贤伟,付娅丽.图像处理技术及其应用[M].北京:国防工业出版社,2005:161-168.

[3] WITTEN I H,NEAL R,CLEAR J C.Arithmetic coding for data Compression[J].Communication of the Association for Computing Machinery,1987,30(6):520-540.

[4] PHILIPPE Desarte,BENOIT Macq,DRIK T M.Singal-adapted multiresolution transform for image coding[J].IEEE Trans.On Information and Theory,1992,38(2):94-97.

[5] 刘萌萌,李华丰.基于小波变换的无损编码算法研究[J].西昌学院学报:自然科学版,2005,19(1):31-35.

[6] KASSIM A A,LEE W S.Color image coding using SPIHT with partially linked spatial orientation trees[J].IEEE Trans on Circuit and Systemfor Video Technology,2003,2(2):203-206.

[7] LI Wei-ping.Overview of fine granularity scalability in MPEG- 4video standard[J].IEEE Transactions on Circuits and Systems for Video Technology,2001,11(3):301-317.

[8] 强鋆焱.基于嵌入式零树小波编码的图像压缩[J].科技风,2010(22):256-257.

[9] 闫凡勇,张颖,张有志,等.基于小波变换的图像压缩技术[J].电脑知识与技术,2010,6(3):698-700.

[10] 夏寅辉,马文波.一种改进的基于小波变换的快速EZW算法[J].激光与红外,2009,39(1):110-112.