利用功率超声技术测量金属材料的杨氏弹性模量
2014-03-22刘蕊
刘 蕊
(必能信超声(上海)有限公司,上海 201613)
0 引言
在很多工程应用中,金属材料的杨氏弹性模量对于结构的设计都是关键而敏感的参数。特别是对于各项同性材料而言,由于描述其弹性性质的独立常数很少,因此其杨氏模量能够很好地反映该材料的力学特性。在功率超声领域,由于超声换能器、调幅器以及工具头都主要使用金属材料,所以杨氏弹性模量对设计的影响非常大,特别是对谐振频率的估算,其准确度会直接影响设计精度和加工的难易[1]。
常规的测试杨氏弹性模量的方法有很多,超声技术作为无损检测的代表技术,已经相当成熟[1,2]。由于材料中的声速并不随着试件外形的变化而变化,所以只要测得材料中的纵、横波速度,就可以求得材料的弹性模量。但是,采集和分辨回波信号并不容易,往往需要信号发射、采集和处理系统来得到测试样品的材料参数,对测试环境要求较高,投入成本也很大。本文提出一种利用超声焊接换能器测量谐振频率的方法,利用金属圆棒的简谐振动,可以较准确地测定材料的杨氏弹性模量。同时,用有限元法对测量结果进行验证。
1 测量原理
1.1 弹性体虎克定律
以铝棒为例,根据弹性体的虎克定律,其杨氏模量和泊松比可以直接由样件尺寸、质量和谐振频率得到。由超声波在圆棒中传播的频率方程可知[3]:
E=C·ρ·f2
(1)
式中:E为杨氏弹性模量;ρ为材料密度;f为指定振动模式下所对应的谐振频率;C为修正系数,同测试样品的形状尺寸、泊松比以及振动模式有关。对于纵向振动模式来说,杨氏模量还可以表示为:
(2)
(3)
式中:n为振动阶数;fn为纵向谐振频率;L为谐振长度;μ为材料的泊松比;De为铝棒直径。
如果仅考虑一阶振动模态即n=1,那么只要得到铝棒在某一长度时的谐振频率,就可以根据方程(2)求得杨氏弹性模量E。
1.2 超声波谐振原理
为了准确测得长度为L的铝棒对应的一阶谐振频率f,需要建立一套谐振系统使测试样件能发生谐振,并测试谐振频率。本文利用功率超声中常用的超声波焊接换能器,通过调整铝棒长度让二者发生共振。理论上只要换能器的频率f已知,那么发生共振时,铝棒的谐振频率也应该是f,当时的长度L即谐振长度,然后应用方程(2)得到铝棒的杨氏弹性模量E。但在实际操作中,存在以下几个问题会给测试结果带来误差:
1)连接问题。在测试铝棒的谐振频率时,为了使测试铝棒和换能器能够刚性连接,两者之间需要用螺丝拧紧。连接螺丝由于材料和螺纹的影响,会给谐振频率带来很大误差。
2)换能器的频率误差。当换能器和铝棒连接后所测得的谐振频率实际上是二者的组合频率,如果换能器本身的谐振频率并不十分精确,那么由此测得的组合频率值会同铝棒的谐振频率值存在很大误差。
因此,采用焊接换能器测试铝棒谐振频率时需要消除以上影响。根据声波在圆棒中的传播特性和圆棒作纵向振动时的频率方程[4,5],得到波速、频率和长度的关系如下:
v=lnfn
(4)
(5)
式中:v为超声波在圆棒中的传播波速;n为振动阶数;ln为波长。
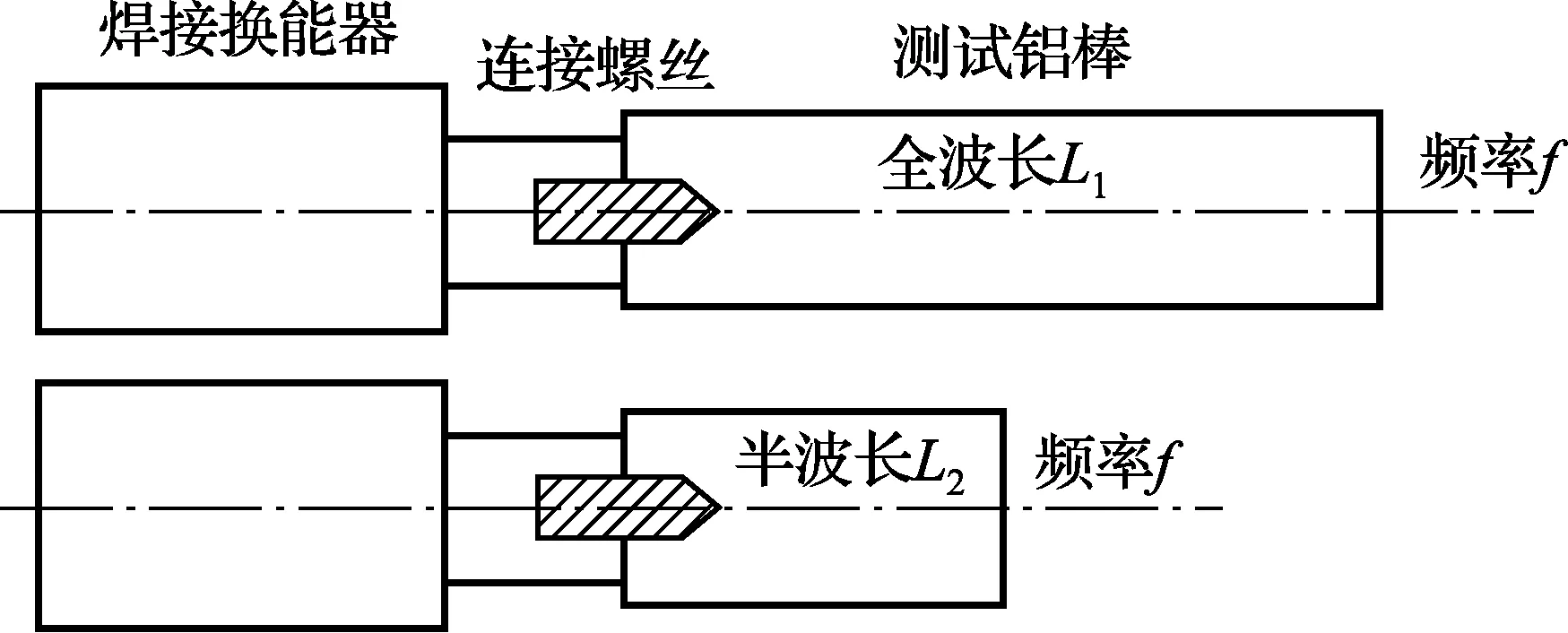
图1 铝棒同换能器连接示意图
2 物理模型
按照该方法,利用40kHz的焊接换能器测试直径为25.1mm的铝棒。未加工前样件的原始长度为141.4mm,质量为0.196 kg,计算得到材料密度为2801kg/m3。如果将铝棒视为均匀材料,那么其纵向振动的谐振频率受泊松比的影响很小,因此值采用经验值0.33。从原始尺寸开始逐渐减小铝棒的长度,并用换能器测出相应的频率值,得到频率长度曲线如图2所示。由插值法得到谐振频率40000Hz时对应的全波长和半波长分别为123.8mm和60.9mm,二者差值62.9mm即为40000Hz对应的准确的半波长度。通过方程(2),计算得到铝棒的杨氏模量为72.44GPa。
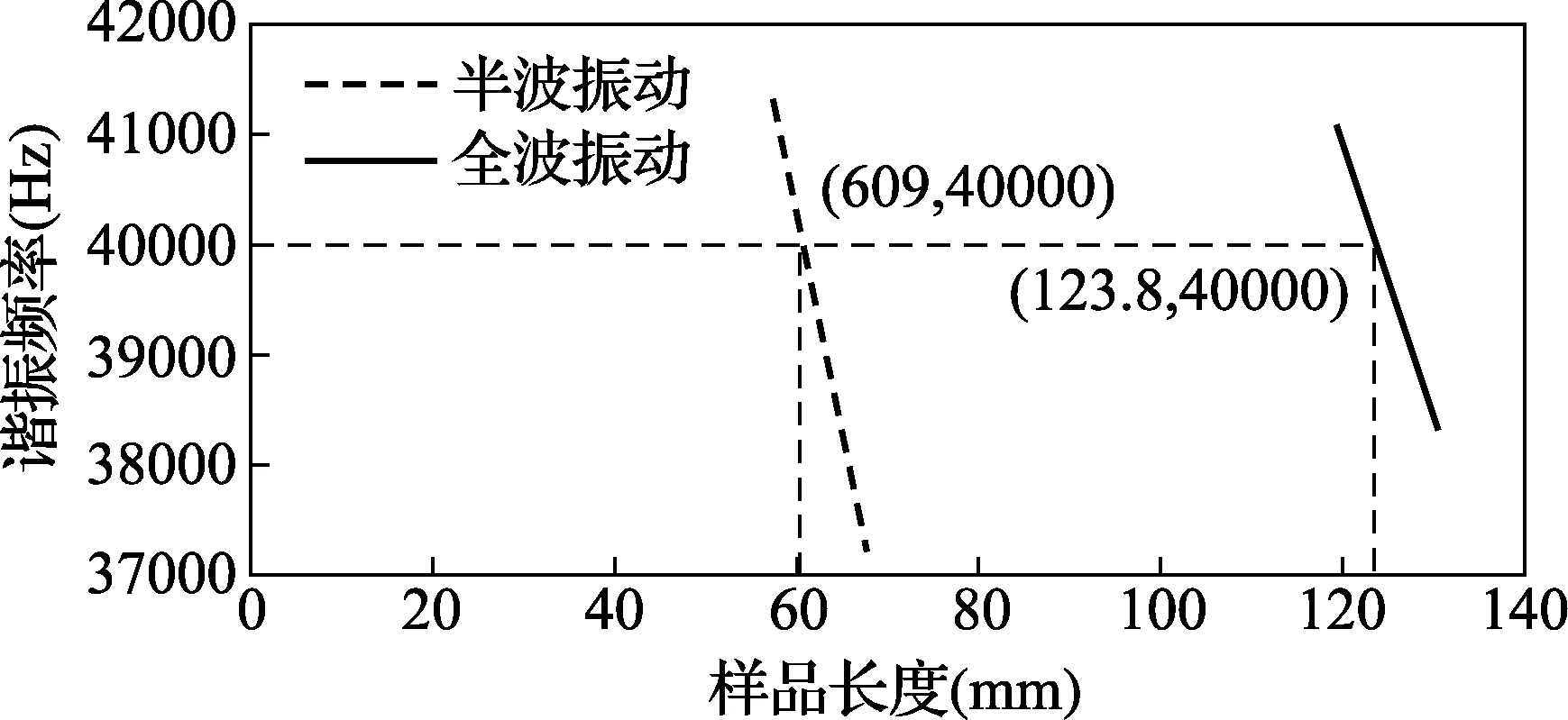
图2 铝棒长度与谐振频率的关系曲线图
3 有限元模型验证
3.1 有限元理论
为了验证测试的准确性,利用有限元软件ANSYS对实验结果进行仿真计算。有限元方法是以变分原理和剖分插值为基础,对实际模型进行离散化、构造插值函数,通过物理上的近似,认为实际点的行为由相邻节点行为的插值关系来描述,于是把实际的物理问题离散化成求解节点未知量的代数方程组求解问题。ANSYS在处理结构力学线性问题所依赖的有限元方程如下:
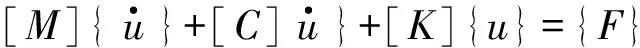
(6)
式中:[M]、[C]、[K]分别为系统的质量矩阵、阻尼矩阵和刚度矩阵,在结构参数(包括几何参数和材料参数)给定,及有限元网格生成后,[M]、[C]、[K]已经完全唯一确定了;{F}是载荷力向量。如果对模型进行模态分析,则{F}={0},根据方程(6),即为方程(7) 有非零解的本征值问题。
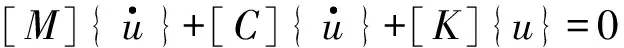
(7)
3.2 仿真结果
ANSYS模型尺寸直径为25.1mm,长度62.9mm,网格划分如图3所示。设定参数如下:材料密度2801kg/m3,泊松比0.33,杨氏弹性模量72.44GPa,得到的半波长谐振频率为39992Hz,振型如图4,与理论值的误差仅为8Hz。

图3 ANSYS中的铝棒模型及网格划分图
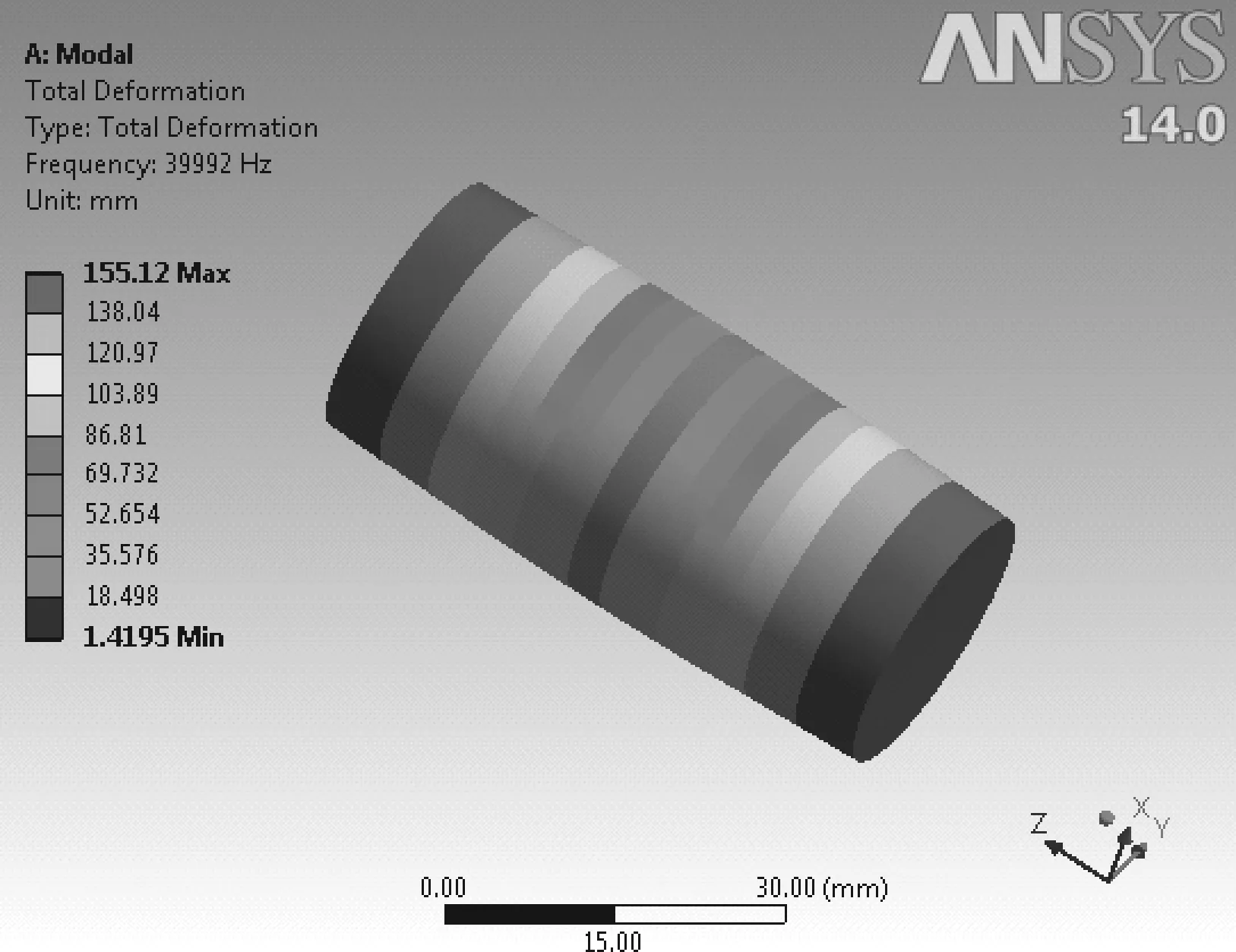
图4 铝棒的半波长简谐振动振型图
4 结论
通过有限元法证明,用超声焊接换能器激发铝棒的简谐振动,根据长度及振动频率的对应关系求得铝棒杨氏弹性模量的方法非常有效,为功率超声设计提供了一种简单方便而且成本较低的测试方法。
[1]冯若.超声手册.南京大学出版社,1999
[2]何存富,周辛庚,戴福隆.一种非接触式测定材料弹性常数的新方法.力学学报,1997,29(6)
[3]ASTM标准E1786,C1259
[4]杜功焕,朱哲民,龚秀芬.声学基础.南京大学出版社,2001
[5]Rose,J L .固体中的超声波.何存富,吴斌,王秀彦译.科学出版社,2004
[6]花世群.利用洛埃镜测钢丝的杨氏弹性模量.计量技术,2002(5)
[7]阮小霞,花世群.用改进的迈克耳孙干涉仪测量杨氏模量.计量技术,2006(8)
