基于模型分析方法的振动加速度计比对数据的处理*
2014-03-22胡红波
胡红波 于 梅 白 杰
(中国计量科学研究院,北京 100029)
0 引言
为了顺应经济全球化发展与消除贸易技术壁垒,国际计量局(BIPM)联合有关国家计量院以及国际组织签署了“互认协议”(MRA)[1],而MRA实施所包含的关键步骤就是国际比对,同时国际比对也是考核实验室能力的有效手段[2-3]。在振动冲击专业计量领域,中国计量科学研究院所建立的基标准装置积极参加并主导国际以及亚太区域的关键比对,有效地支撑了我国校准及测量能力(CMCs)的认可,相关的检测与校准能力已经在BIPM网站上关键比对数据库(KCDB)中公布[4]。
对于振动与冲击计量专业的国际关键比对,通常都选择性能较好的压电加速度计作为传递标准,在规定的频率范围与幅度下以加速度计的灵敏度作为比对量。BIPM推荐的评估指南(The Evaluation Guidelines)[5]确定了完整的分析与处理比对数据的方法。该方法规定了如何由比对的测量数据确定比对参考值以及评价参比实验室校准能力一致性的方法。关于如何确定比对参考值,一直是本领域国内外研究的热点问题之一[6-9],本文介绍了一种基于模型分析确定加速度计比对参考值的方法。该方法不同于BIPM推荐的评估指南所推荐的将各个频率点的灵敏度由参比数据单独计算,而是基于加速度计的物理结构建立了频率与灵敏度的数学模型,利用参比实验室提供的测量结果与对应的不确定度,采用加权最小二乘算法计算得到模型的参数,从而可以得到在给定频率范围内任意频率点的灵敏度。本文利用上述两种方法对亚太计量规划组织(APMP)加速度计振动校准比对的数据进行了处理,一致的参考值证明了该方法的有效性,同时由于利用了加速度计的物理模型等信息,通过模型计算得到参考值对应的不确定度比采用指南推荐方法得到的不确定度更小,更小的不确定度增大了发现不一致参比数据的可能性,这也进一步验证了基于模型分析的方法在一定条件下的优越性。
1 加速度计校准区域关键比对数据
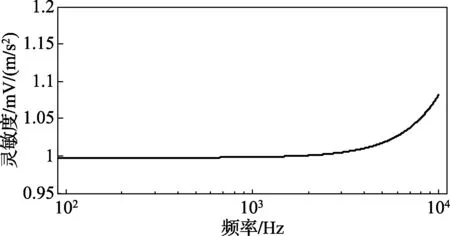
对于振动冲击专业的区域或者国际比对,加速度计(包括或者不包括配套放大器)通常作为传递标准器具,由各个参比实验室在规定的频率范围内,比如10Hz~10kHz,用各自的振动标准装置确定其对应频率点的灵敏度值与测量不确定度。本文研究的数据来源为亚太计量规划组织的振动关键比对[10],本次比对的标准器为丹麦B&K公司生产的型号为8305的标准加速度计与型号为2626的放大器。亚太地区共有5个实验室参与,外加欧洲的德国联邦物理技术研究院(PTB),总共有6个实验室参加了比对,比对的频率范围为100Hz~10kHz。其提交的加速度计灵敏度数据与对应的不确定度如图1与 图2所示。比对详细的情况可见参考文献[10]。
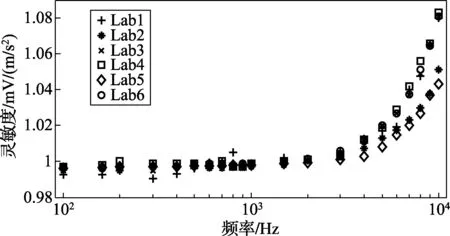
图1 用于分析的关键比对数据
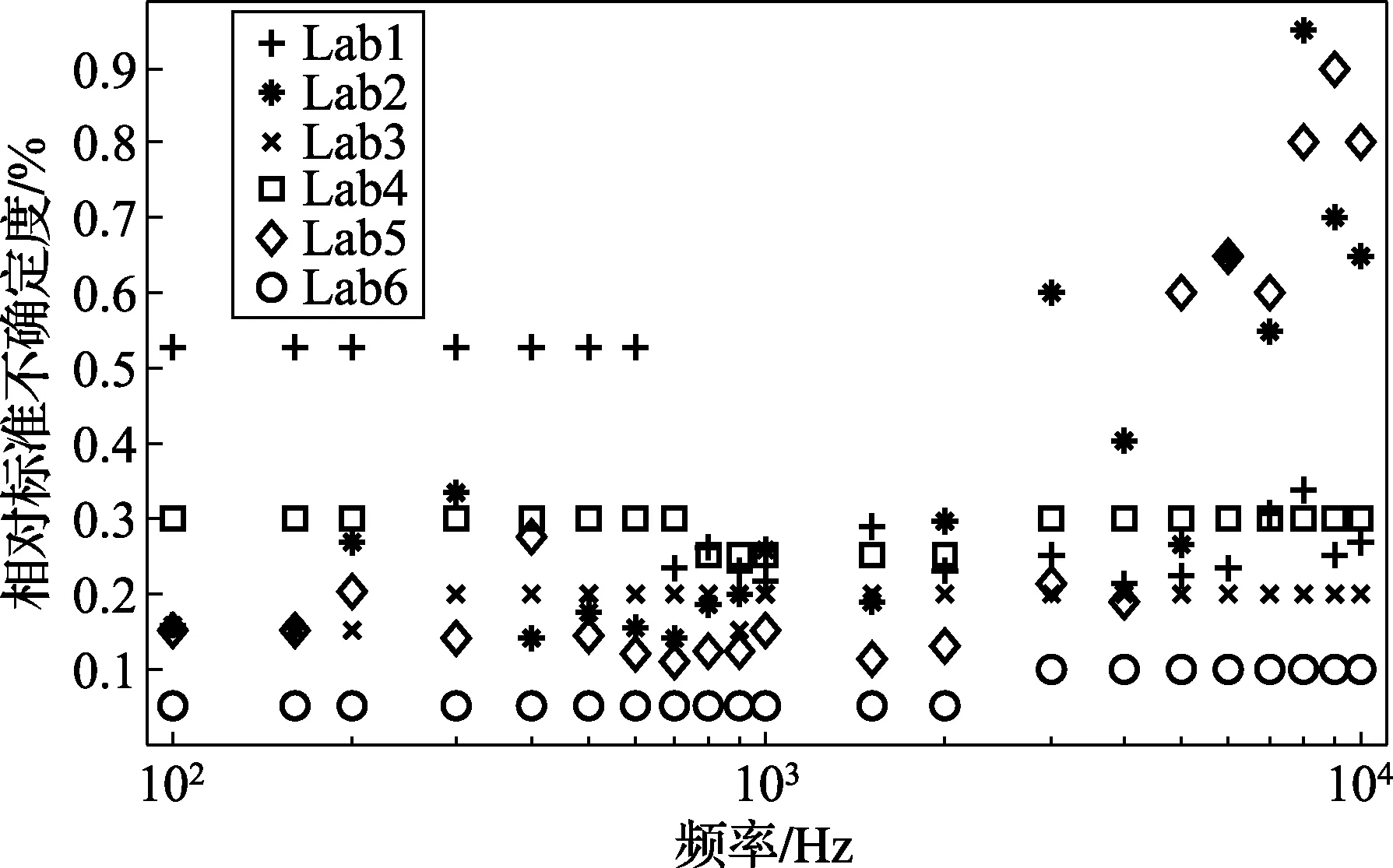
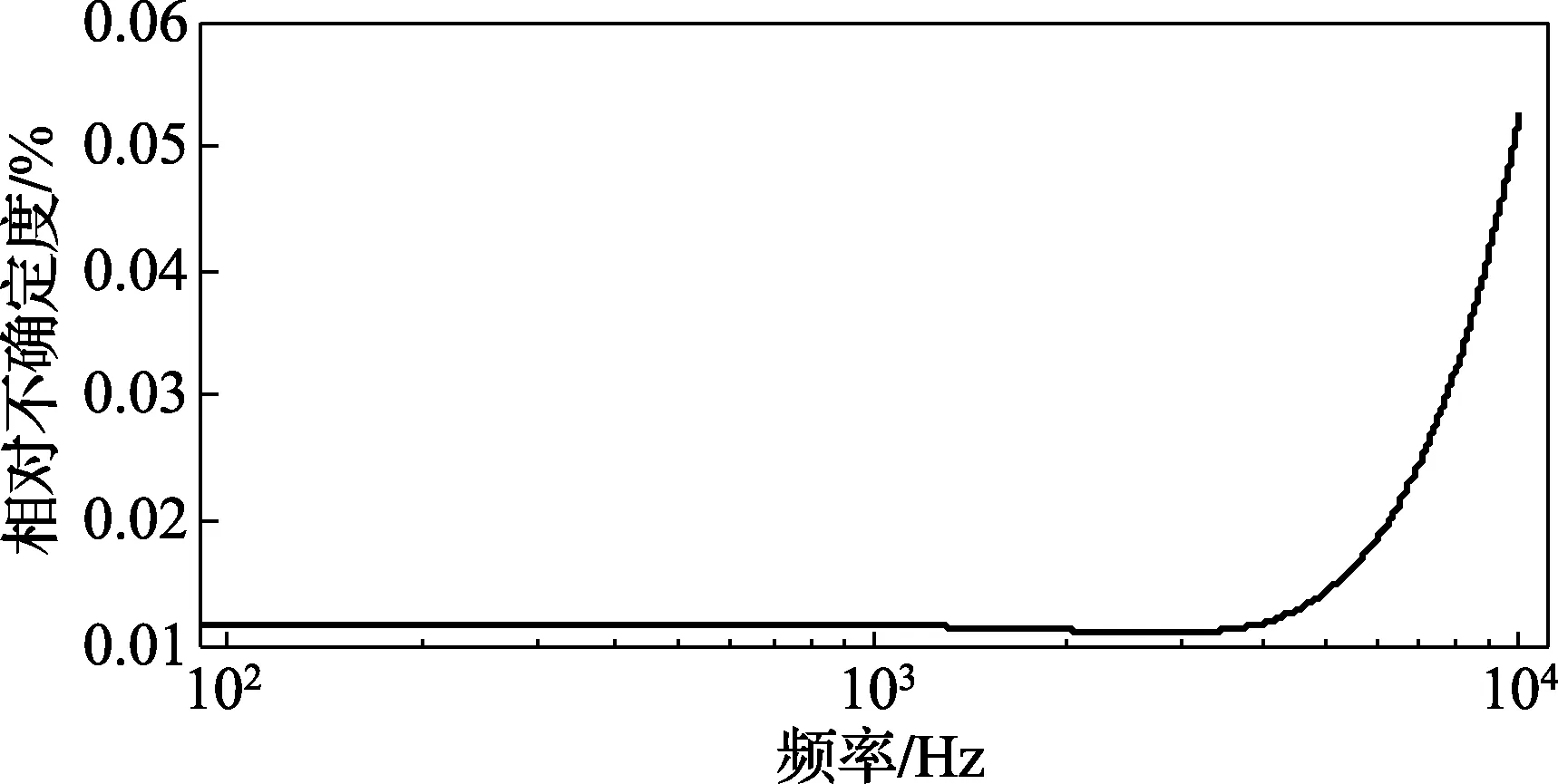
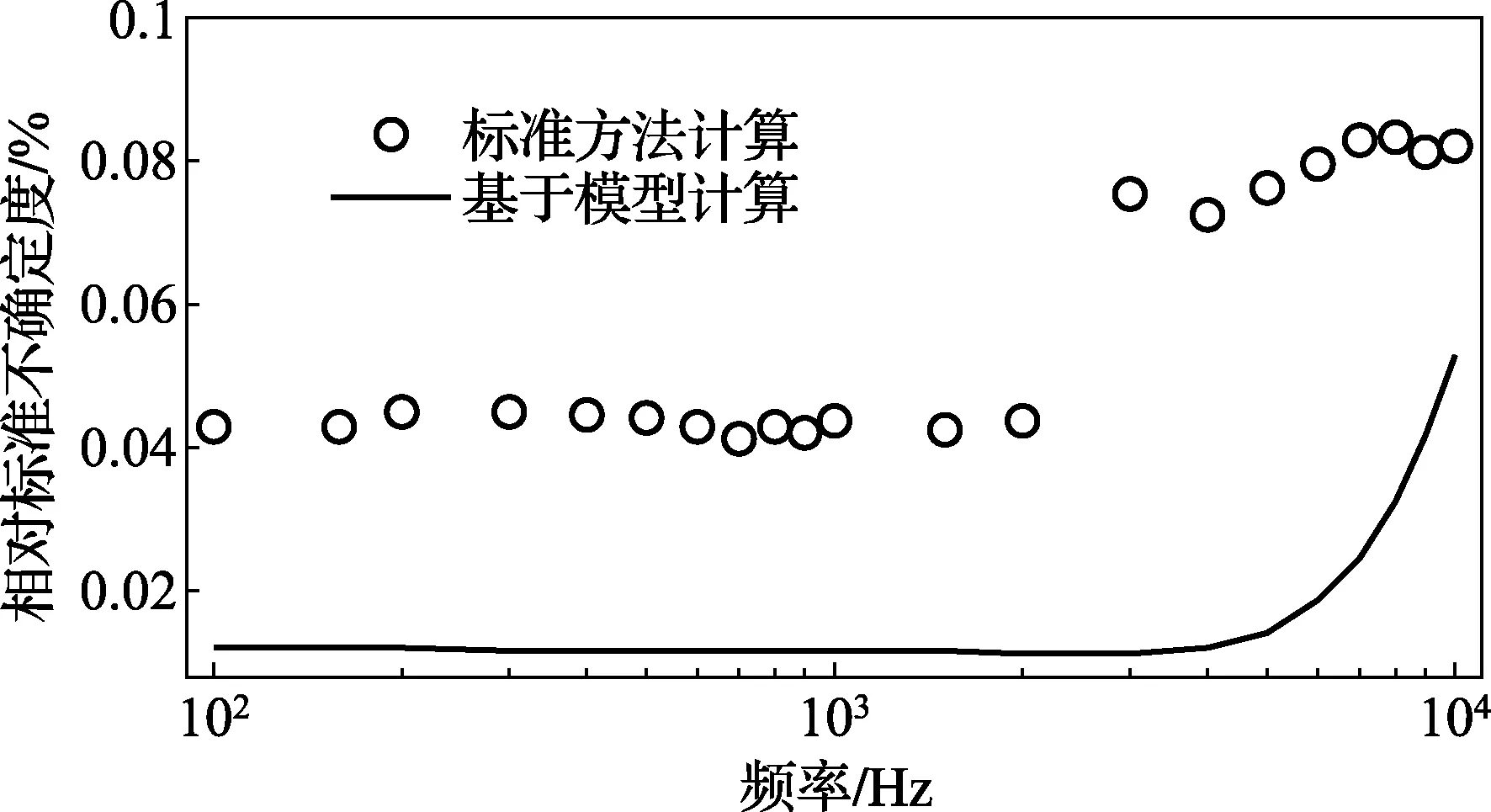
图2 比对数据对应的标准不确定度
通过比较上述数据可以发现,对于频率范围较高的部分,特别是频率点7,8,9,10kHz时,比对实验室2与实验室5的数据明显偏小,初步分析可能是因为该实验室标准装置的系统偏差所致,按照参考文献[10]的建议,在下面的两种方法分析参考值与对应不确定度时,这两个实验室在以上4个频率点的数据未参与对应频率点参考值的计算。另外还需要说明的是在不同的频率点不同实验室测量结果是相互独立的。
2 指南推荐分析方法
依据BIPM指南推荐的方法,对于每一个频率点的灵敏度参考值采用分别计算的方式。设s1,s2,…,sn为各个参比实验室在某一频率点的灵敏度测量结果,u(s1),u(s2),…,u(sn)为其对应的标准不确定度,且sref,u(sref)为该频率点灵敏度参考值以及对应的不确定度。按下式采用加权平均方式即可计算得到参考值与对应的标准不确定度。
(1)
(2)
按照上述计算方式对比对的数据进行处理,在比对的频率范围内分别得到的各频率点的灵敏度参考值与对应的标准不确定度如图3、图4所示。
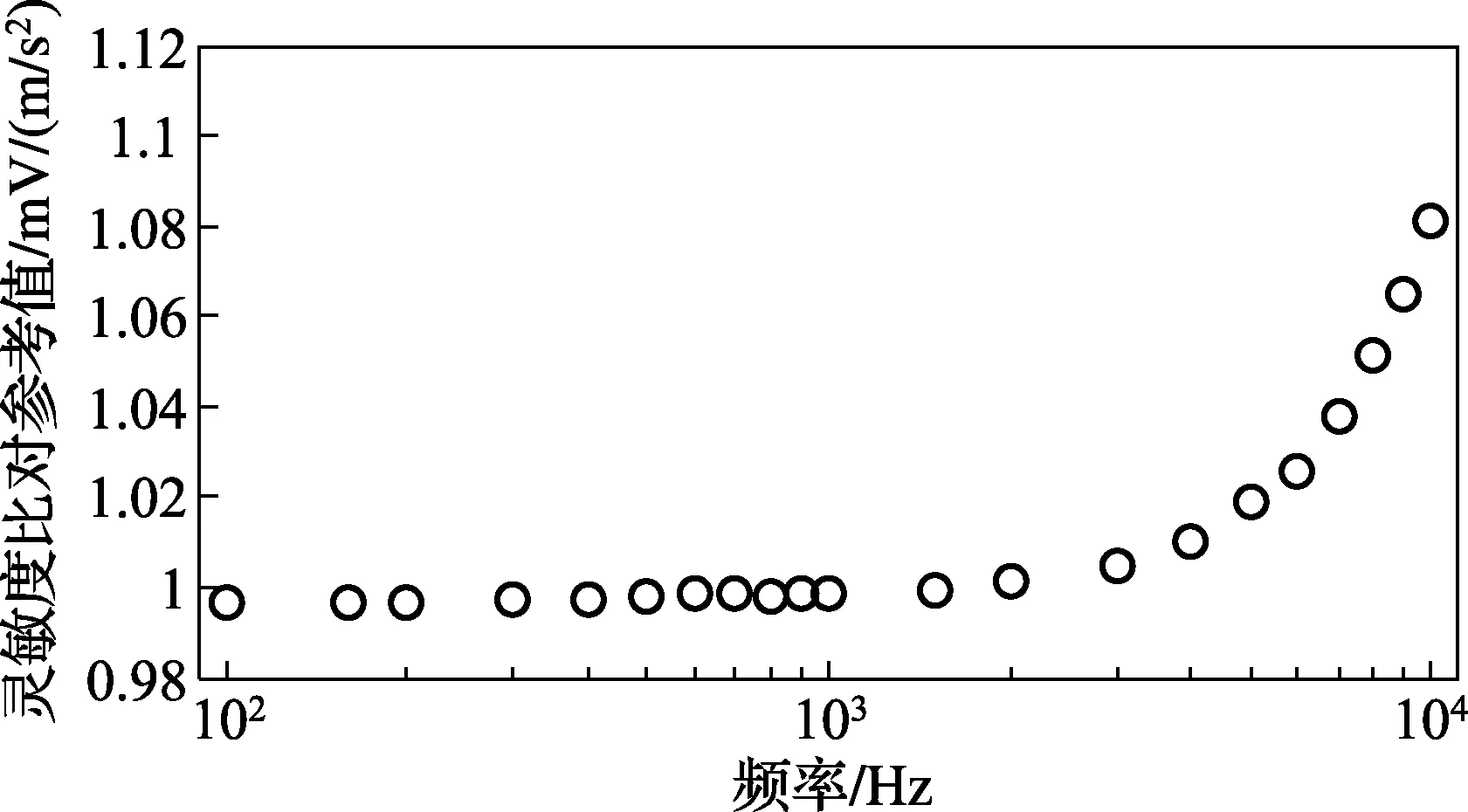
图3 指南推荐方式计算所得到比对参考值
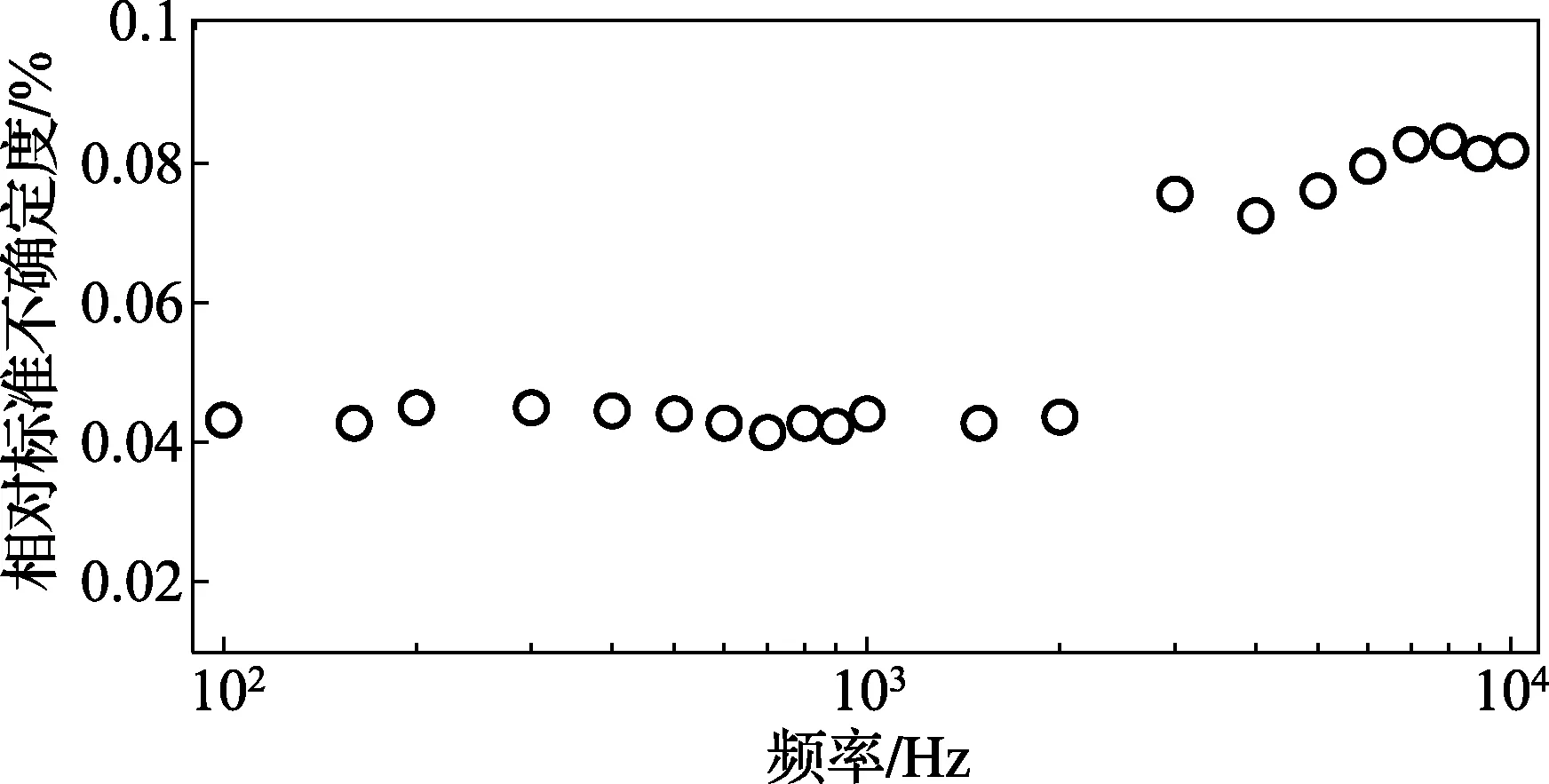
图4 参考值对应标准不确定度
根据指南推荐的评价比对实验室测量结果的方法,采用各实验室测量的结果与参考值的偏差以及该偏差的不确定度(95%的置信概率)来定量的描述。测量结果的一致性评价用En值来表示,按式(3)计算。
(3)
即En值为比对值与参考值之间的偏差除以该偏差的扩展不确定度。上式中,k为扩展因子,u(si-sref)为偏差的标准不确定度。需要特别说明的是,在计算u(si-sref)时,必须考虑比对值si与参考值sref之间的相关性。En的绝对值越大,则表明比对值与参考值越不一致。一般来说,对于单一测量点比较的En计算,通常偏差量为正态分布,置信概率约为95%时取k=2,此时若:
|En|≤1
(4)
则表明两者之间是一致的。但有时利用此规则判断一个测量数据是否一致时也会有些问题,比如两个En值,一个为0.99而另一个为1.01,则会得出相反的结论,而实际有可能两个测量值的差别非常小。考虑到本次比对每个参加实验室的测量点个数为N=21,为了避免出现个别测量点的En值超过单位1,覆盖因子k应增大以确保所有21个测量点的En值小于或者等于单位1的概率均为95%。由于各个频率点测量值与对应的En值均不相关,故可按式(5)来计算k值。
(5)
上式中,Φ为标准正态分布,查正态分布表可得k=3.03≈3。
为了按式(3)计算En值,依据GUM不确定度评估准则可得:
u2(si-sref)=u2(si)-2u(si,uref)+u2(sref)
=u2(si)-2u2(sref)+u2(sref)
=u2(si)-u2(sref)
(6)
从而可计算偏差所对应的标准不确定度。综上可计算得到参比实验室的En值如图5所示。
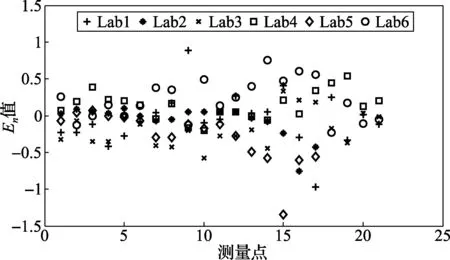
图5 标准方法计算得到En值
从En图可以看出,只有实验室5的第15个测量点En大于1,即该实验室在频率为4kHz时的测量结果与其他实验室是不一致的。
3 基于模型的分析方法
加速度计是利用惯性力来测量物体运动的,其结构通常由外壳、质量块、压电晶体以及限制质量块与外壳之间相对运动的弹簧构成。通常,我们认为加速度计是一个线性的动态系统,在其线性动态范围内可将其等效为一个单自由度的弹簧质量系统,并用一个二阶的LTI系统来对其进行描述[11-12],典型的幅频响应曲线如图6所示。

图6 加速度计典型幅频曲线
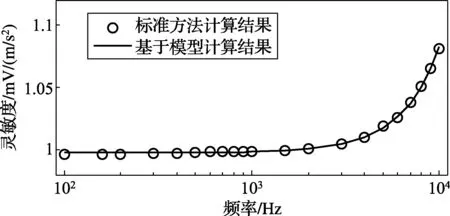
当fmax (7) 式中:S0为加速度计零频时的灵敏度;f0为谐振频率;Gf为配套放大器的频率响应。 (8) 式中:sf,i表示第个实验室在频率为下测量的结果;u(sf,i)表示其对应的标准不确定度。 (9) 图7 基于模型计算得到的参考值曲线 图8 对应参考值的标准不确定度 =X(XTV-1X)-1XTV-1cov(Y,Y) =X(XTV-1X)-1XTV-1V =X(XTV-1X)-1XT 图9为采用模型计算得到的参考值与对应的不确定度,按式(3)计算得到的En值图。 图9 由模型计算得到的En值 从En图可以看出,实验室5的第15个测量点和实验室1的第17个测量点En值绝对值大于1,即实验室5在频率为4kHz时的测量点与实验室1的6kHz测量结果与其他实验室不一致。 图10与图11为两种方式计算比对参考值与对应标准不确定度的比较图。从该图可以看出,两种方式计算得到的参考值基本一致,这证明了利用模型计算参考值的有效性,同时利用模型计算得到参考值对应的标准不确定度却小很多,也说明了基于模型的计算方式在一定条件下是可靠的。 图10 两种方法计算得到参考值的比较 图11 两种方法计算标准不确定度比较 对两种不同分析方式的比较可以看出,基于模型的分析方法得到的参考值比较好,主要的原因在于该方法利用了基于频率与灵敏度的数学模型表达式等信息。两种方法得到En值的结果基本一致,利用指南推荐分析方法得到的一个大于1的En值,在基于模型的分析方法中也得到了同样的结果,并且在指南推荐的分析方法中一个很接近于1的En值在基于模型分析的结果中则大于1。另外,如果将两种方式得到的En值画成X-Y图形,则会发现两者是相关的,这说明在一定条件下,两种方法的结论是一致的。 本文主要论述了一种基于模型处理比对数据的分析方法,该模型基于加速度计的物理结构,在一定的频率范围内能完整地描述频率与灵敏度之间的关系。通过采用加权最小二乘算法计算出了模型的参数,从而得到了比对参考值与对应的标准不确定度。通过与BIPM评估指南推荐方法计算的结果进行了比较,结果的一致性证明了该方法可靠有效,并且其更小的不确定度表明在一定条件下基于模型分析方法的优越性。目前国际上本专业领域对应的技术委员会正在起草有关采用激光绝对法进行加速度计参数辨识的ISO标准[13],相信该标准文件的出台对于加速度计特性校准比对能起到一定的积极作用。 [1]于亚东,倪晓丽.MRA中的国际比对与标准物质[J].中国计量,2002(1):7-10 [2]中国计量测试学会组编.一级注册计量师基础知识及专业务实[M].北京:中国计量出版社,2011 [3]胡红波,孙桥,黄宇中.不同冲击激励系统绝对法冲击校准比对可行性的研究[J].振动与冲击,2012,31(20):27-31 [4]BIPM.The BIPM key comparison database website[EB/OL].2013-08-23.http://kcdb.bipm.org/default_fr.asp [5]W Bich,M Cox,T Estler,et al.Proposed guidelines for the evaluation of key comparison data[R].BIPM Director’s Advisory Group on Uncertainties,2002 [6]M G Cox,P M Harris.The evaluation of key comparison data using key comparison reference curves[J].Metrologia,2012,49:437-445 [7]Maurice G Cox.The evaluation of key comparison data:determing the largest consistent subset[J].Metrologia,2007,44:187-200 [8]吴书清,吉望西,刘达伦,等.绝对重力仪国际比对现状[J].地球物理学进展,2009,24(2):768-773 [9]H Moeck,C Elster,A Link.Analysis of comparison data from acceleration measurements[J].Measurement Techniques,2003,46(5):523-528 [10]C Chen,H-J von Martens.APMP.AUV.V-K1 Regional key comparison of standard accelerometer.Final report,project number APMP-IC-4-95(2000) [11]胡红波,于梅.基于高冲击激励的加速度计参数辨识的研究[J].传感技术学报,2012,25(4):487-491 [12]樊尚春.传感器技术及应用[M].北京:北京航空航天大学出版社,2004 [13]Thomas Bruns,Afred Link,Franko Schmahling,et al.Calibration of accelerometers using parameter identification -Targeting a versatile new standard[R].XIX IMERO World Congress.Fundamental and Applied Metrology,September 6-11,Lisbon,Portugal,2009
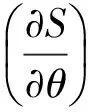
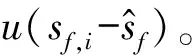
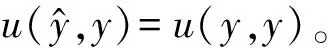

4 两种方法的比较与分析
5 小结
