增加日历时间因素的动态利率模型

许 宁，高 涓，张大为

（1.辽宁大学经济学院，辽宁沈阳110036；2.苏州大学 东吴商学院，江苏 苏州 215021；3.沈阳药科大学工商管理学院，辽宁沈阳 110016）

增加日历时间因素的动态利率模型

许 宁1，高 涓2，张大为3

（1.辽宁大学经济学院，辽宁沈阳110036；2.苏州大学 东吴商学院，江苏 苏州 215021；3.沈阳药科大学工商管理学院，辽宁沈阳 110016）

考虑到中国金融监管当局对金融机构监管措施的特点，在利用传统均值回复动态利率期限结构模型（CKLS模型）分析我国短期利率变动特点时，有必要结合中国货币市场利率季度末飙升的特点，在传统模型基础上增加日历时间因素（CTF），利用银行间债券回购交易市场和上海证券交易所债券回购交易市场利率为样本的分析结果表明，通过扩展后的短期利率动态模型对短期利率的变动具有更大的解释能力，且银行间市场利率受到日历时间因素的影响更显著，但是其均值回复速度较慢，而上交所回购市场利率受到日历时间因素的影响不显著，但是其利率在偏离均值后，回复到均值的速度更快。市场参与主体和交易机制等的不同是造成两种市场不同特性的原因。

动态利率期限结构；日历时间因素；债券回购利率

一、引言与文献回顾

利率作为连接产品市场和货币市场的纽带，在现代经济和金融中发挥举足轻重的作用，它是金融产品定价、金融机构风险管理以及经济预测和分析的最重要基础。利率期限结构是某一时点（t），反映不同到期期限T及其对应无风险利率关系的表达式，一般用R（t，T）表示。利率期限结构和通常所说的国收益率曲线意义不同，后者是虽然和前者在形态上类似，但是意义存在实质性的差别。利率期限结构在不同时刻会表现出不同的形态，有水平形态的，上升形态和下降形态等。金融和经济学家一直致力于研究期限结构的变动原因以及其影响。

传统利率期限理论分别从不同的角度去解释期限结构。其中预期理论认为期限结构反映了投资者预期未来的即期利率的变化。流动性偏好理论认为投资者偏好短期债券，而远期利率等于预期利率加上风险溢价，故长期利率高于短期利率。而市场分割理论认为期限不同的债券市场没有关联性，不同市场被完全分割，每一组期限利率有自己独立的市场均衡。

现代利率期限结构理论根据经济学、金融学以及数学的理论对期限结构进行定量的分析。其主要分为静态模型和动态模型两大类。

静态模型是利用当前或者历史付息债券价格信息，提取期限结构的方法。具有代表性的包括：息票剥离法和NS—S扩展模型。Fama和Bliss（1987）将利息支付（息票）从债券中剥离出去，然后在此基础上来估计无息票债券利率水平，其核心思想就是利用当前债券价格信息，通过从短期到长期利率的迭代运算来计算利率期限结构。杨宝臣和李彪（2004）为解决应用息票剥离法通常会遇到的两个问题:债券非流通性和缺失数据点，用主干点附近平均收益率数据来代替原始主干点收益率，形成了广义的息票剥离法。静态估计利率期限结构的另外一种思路是，先假定期限结构的方程，然后利用历史数据估计方程的参数的、代表性的有Svensson（1994）在Nelson

Siegel（1987）的基础上建立的NS-S扩展模型。该模型能够用较少的参数刻画不同形态的利率期限结构，是目前静态估计中最常用的利率期限结构模型。

利率期限的动态模型是研究利率期限结构如何随时间的动态变化而变化，以及影响变化的因素的模型。它又分为建立在历史数据基础上进行参数估计的均衡模型和利用无套利定价原理的无套利模型。

均衡模型是一种由均衡分析方法得出的模型，它从宏观经济模型出发，推导出短期无风险利率的一个动态变动过程，然后寻找该过程对债券价格以及期限结构的意义。

单因素动态利率期限模型的一般形式是：假设瞬时无风险利率 r遵循如下的变动过程，其中dz为标准布朗运动。在t时刻，T时期到期的零息债券价格P是r,t和T的函数。根据伊藤引理，作为r和t以及T函数的债券价格 P（t，r，T），其瞬时变化 dP 满足利率风险的市场价格q(t，r)表示为假设风险市场价格的表达式为q(r，t)，由伊藤引理可计算和的表达式，通过求解偏微分方程，得到的解析解P(t，r，s)，然后利用利率和债券价格的关系即可得到利率期限结构的表达式。CKLS（1992）对单因素模型进行了一般化的概括，CKLS模型具有均值回复和利率变化波动率随利率水平变化的特点。马晓兰和潘冠中（2006）综合多个著名的单因子利率期限模型，并在此基础上提出了一个新的一般模型，。其漂移项包括线性和非线性两个部分。并用广义矩方法对该综合模型进行参数估计，对比不同模型形式的多种指标的表现，马晓兰和潘冠中（2006） 认为模型：是最符合中国利率市场的动态模型，该模型的具有均值回复的特征，但是回复速度会随利率水平的变动而变化，利率波动对利率水平十分敏感。

二、模型设计

本文在传统CKLS动态模型的基础上，增加了日历时间因素。由于中国金融监管部门在季度末都会对金融机构进行资本充足率、存贷比等方面的审查，因此在季度底，利率往往明显上升，尤其是在2011年之后，每当季度末临近，短期利率都会有一个明显飙升。因此，我们在CKLS模型基础上增加了日历时间因素，而且，日历时间对于利率的影响是非线性的，本文采用当时日期距离季度末天数的倒数来分析日历时间因素的影响。模型另外做如下假设：

A.1：瞬时短期利率r（t）遵循一个连续时间的马尔科夫过程，即扩散过程（DiffusionProcess）。

A.2：t时刻，到期期限为T（T＞t）的零息债券价格P由瞬时利率r（t）以及到期期限T决定。

A.3：市场是有效的。交易成本为零，所有参与者能够同时得到所有信息，并且每位投资者都是理性的。

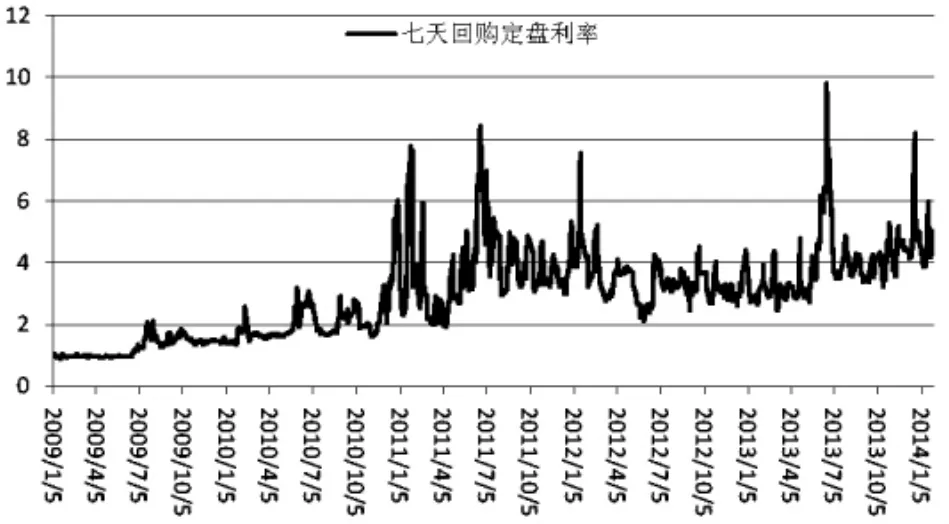
图一 银行间回购市场日定盘利率走势图

在以上假设基础上，短期瞬时利率r（t）的变动过程如下：

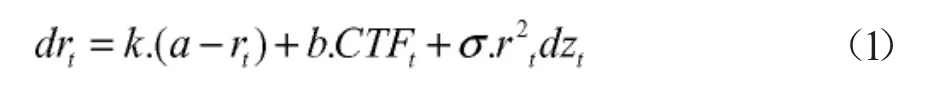
其中0＜ρ＜1,k＞0.dz是标准的维纳过程。CTF为日历时间因素，，QEDay为t日所对应的季度末日历日期，比如，t日为2013年 1月8日，则为2013年3月31日①为避免0作为分母，季度末当日的设定为1。。从中国货币市场历史数据发现，短期利率波动和利率水平的二次方呈现最强的相关性，因此波动项采用的形式，如此设定波动项将简化模型的估计，而且从国内学者的实证分析结果看，CKLS模型中利率波动项中r的指数估计值均在2附近。在模型（1）中，k代表短期利率向其移动均值EMA收敛的速度，k越大，r偏离均值后很快向均值靠拢。由于模型（1）不能求解出R（t，T）的利率期限结构，本文仅分析短期利率动态变化的模型。

本文采用银行间市场和上交所七天回购定盘利

率作为样本数据，银行间市场定盘利率是外汇交易中心在每个交易日上午9:00-11:00之间的全部成交利率为计算基础上，计算出来的成交利率的中位数。上交所回购定盘利率是上交所剔除回购到期日为非交易日因素的七天质押式回购加权成交价格。其计算方法为：

其中:首期结算日＝首次交易日后的第一个工作日,到期结算日＝回购到期日后的第一个工作日,回购到期日＝首次交易日+回购品种天数。若该日非交易日，顺延至下一工作日,若该回购品种当日无交易，则定盘利率取上一交易日的定盘利率。

上述两市场的定盘利率较回购收盘利率能更加准确的反映当时货币市场的真实利率水平，因此本文选用定盘利率作为样本数据，并分别用银行间质押式回购市场七天定盘利率（fr007）和上交所七天回购定盘利率(sxr007)来估计模型。

在进行模型估计之前，首先需要把原始的利率数据转化为等价的年化连续复利利率，计算公式为：由于本文采用7天的利率作为样本数据品，故此处，并据此对原始数据进行连续福利年化处理。

遵循CKLS[1992]的做法，用欧拉离散模型来近似连续利率时间模型。

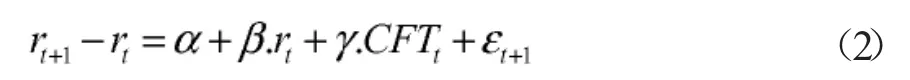
公式（2）中的这种离欧拉散化处理，假定利率变动的方差直接依赖于利率水平，这在某种程度上与连续模型相吻合。模型（2）是对模型（1）的近似离散化，但由于本文采用7天利作为样本，这种短的时间框架内来分析利率的动态变化是，这种误差所产生的影响基本上可以忽略不计。

样本数据分别来自中国外汇交易中心和上海证券交易所。经过连续复利处理后的数据统计信息如表1所示。

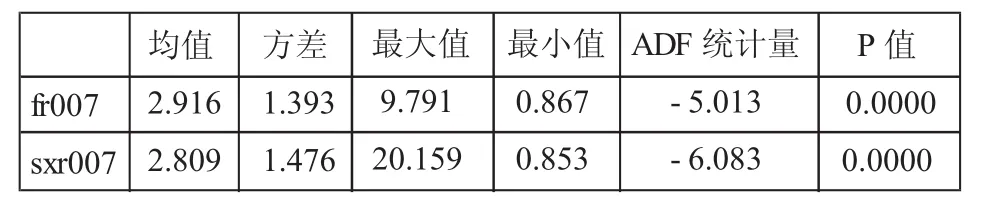
表1 样本数据统计

上面的两个利率数据看，两个样本数据的时间序列均通过了平稳性的ADF检验。上交所利率（sxr007）均值略低于银行间市场利率（fr007），但是波动率更大。主要原因两者的参与主体不同所致，本文之后将做详尽分析。

三、模型估计结果及分析

本文运用Eview6.0对模型（2）进行估计，模型估计结果如下：

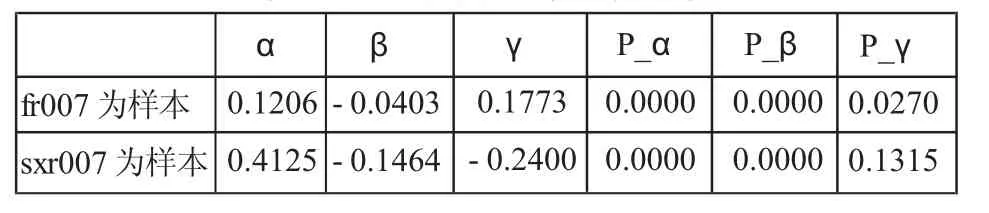
表2 模型（2）的系数估计值及其P值

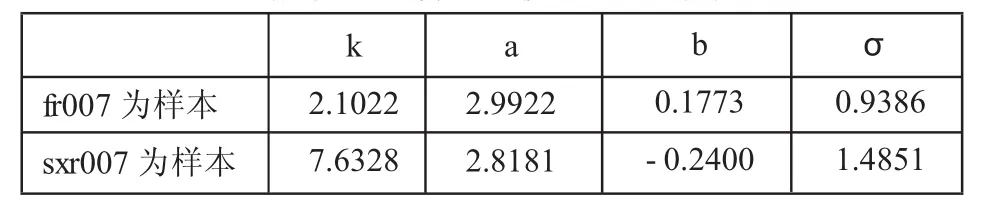
表3 根据（2）计算出的模型（1）的系数

从估计结果可以看出，无论是以银行间市场回购定盘价（fr007），还是以上交所回购定盘价（sxr007）为样本，其对应的瞬时短期利率动态方程（1）的回归速度系数k均大于0，且估计是显著的，表示在中国的货币市场中，短期利率的波动存在向均值回归的规律。以上交所为例，k=7.6328，意味着，若在第一天利率偏离其均值幅度达到10%，均值回复的因素在第二天将推动利率反向变动1.46%（k*δ）。利率偏离降低至5%需要5天，而银行间市场，利率偏离均值10%，需要17天才能纠偏至5%。

从模型（6）的估计结果看，以银行间市场七天回购定盘利率为样本的估计结果，其日历时间因素的系数b为0.177，这意味着，若距离季度末还有6天时，日历时间因素对第二天利率变动的影响平均为0.0059。在临近季度末的一个月内，CTF对于利率变动影响幅度会随着季度末的临近而加速上升。因此，在分析银行间市场短期利率波动时，不能忽视日历时间因素的影响。

图二银行间回购市场CTF在季度末对于利率变动的影响

但是以上交所七天回购定盘利率为样本的估计结果看，系数γ的P值为13.15%。估计结果不显著，同时γ的估计结果为负值，这表示上交所七天回购利率受到日历时间因素的影响不明显。

另外，以fr007为样本的估计结果，其短期利率回归速度指标k要小于以sxr007样本估计的k值，短期利率在偏离均值后，回到均值速度较慢。说明，银行间市场利率短期趋势性强于上交所回购市场。短期利率变化的标准差项σ，以fr007为样本的估计值也高于以sxr007为样本的估计值，表明上交所回购市场利率的变动也存在更大的波动性。

之所以造成不同样本估计结果的差别，主要是和两市场的构成以及运行机制的差别有关。银行间回购市场参与者主要包括银行、基金、保险、券商、特殊结算机构等,个人投资者无法参与其中。交易所债券回购市场参与者不包括银行,但包括个人投资者、基金、保险、券商、一般企业法人等；银行间市场资金融出方主要是全国性商业银行,融入方主要是城市商业银行、外资银行、证券、基金和保险;交易所市场资金融出方主要是个人和一般法人,而融入方主要是保险等。此外，在交易机制方面，银行间回购市场采用一对一的询价方式，更加适合合格机构投资者之间批发类的大宗资金往来，交易所的集中撮合融资方式更适合较小的机构投资者和个人融资，其交易灵活性更大。

在我国，银行仍是最重要的金融中介机构，银行若不能参与证券交易所债券回购交易市场，势必造成交易所市场资金供给的波动较大，同时交易所市场有大量的个人以及企业投资者参与，另外，证券交易所市场利率水平和股市的上涨和下跌有着更为直接的联系，因此交易所回购市场利率的波动要大于银行间市场。

四、总结与政策建议

本文在CKLS模型的基础上加入了类似于季节性因素的日历时间因素，并对比了银行间和上交所回购市场利率的动态模型，结果显示，两市场的均值回归特性均十分显著，但是由于两市场参与主体、交易机制等的差异，导致量市场利率变动均值回复速度出现明显不同。银行间市场均值回复速度较慢，一旦利率较大幅度的偏离均值，其需要较长的时间才能回复至均值附近水平。本文提出的日历时间因素对于银行间回购利率的影响是显著的，但是其影响幅度较小，不能充分的解释利率在季度末期飙升的现象。

考虑到利率在金融市场和商品市场中的基础性地位，鉴于我国两个重要的货币市场——银行间回购交易市场和交易所回购交易市场——的利率平均水平和利率波动特性存在较大的差别，这不利于我国形成统一的基准利率。我们呼吁在利率市场化的进程中，应该及时将两市场进行融合，让所有的经济主体都可以公开、平等地参与两个货币市场，同时应该统一清算和监管。只有这样，才能形成真正反映经济和金融体系资金供需关系的利率，也有助于央行按照这种统一的利率变动进行货币调节，并刺激利率衍生品市场的快速发展。

[1]Ang A,PiazzesiM.A no-arbitrage vector autoregression of term structure dynamics with macroeconomic and latent variables[J]. JournalofMonetaryeconomics，2003，50(4):745-787.

[2]Litterman R B,Scheinkman J.Common factors affecting bond returns[J].The Journalof Fixed Income,1991,1(1):54-61.

[3]Longstaff,Francis A.and Eduardo S.Schwartz.Interest-rate volatility and the term structure:a two-factor generalequilibrium model[J],Journalof Finance,1992,48:1259-1282.

[4]Nelson CR,SiegelA F.ParsimoniousModelingofYield Curves[J]. The JournalofBusiness,1987,60(4):473-489.

[5]Svensson LEO.Estimatingand interpreting forward interest rates: Sweden 1992-1994[R].National Bureau of Economic Research, 1994.

[6]Vasicek O.An equilibrium characterization of the term structure [J].Journalof FinancialEconomics，1977，5(2):177-188.

[7]马晓兰，潘冠中.单因子利率期限结构模型的广义矩估计及对中国货币市场的实证检验 [J].数量经济技术经济研究,2006,23(1):107-116.

[8]杨宝臣，李彪.基于广义息票剥离法的国债收益率曲线的估计[J].中国管理科学，2004，12(6):1-5.

[9]朱世武，陈健恒.交易所国债利率期限结构实证研究[J].金融研究，2003，10:63-73.

【责任编辑 李 菁】

F224

A

1674-5450（2014）05-0058-04

2014-04-15

许宁，男，安徽六安人，辽宁大学金融经济学博士研究生。