基于STFIGARCH模型的权证定价研究

邹 平， 肖庆宪

（上海理工大学管理学院，上海 200093）

1 文献综述

1.1 波动理论

人们对利空消息的反应程度常高于对好消息的反应程度，金融时间序列的显著特征之一就是波动对冲击的非对称反应.负的冲击相比正的冲击，产生更大的波动，即“杠杆效应”.为了衡量波动的非对称性，有许多模型被提出：如Nelson［1］提出EGARCH模型，Glosten等［2］提出GJR模型，Engle［3］提出AGARCH模型等.但是用信息冲击曲线（Engle和Ng［4］）来分析信息冲击对波动的影响，所有这些模型只有两种状态：正的冲击产生低波动和负的冲击产生高波动.Hagerud［5］，Lee和Degennaro［6］，Lubrano［7］扩展了这类模型，在方差方程中引入平滑转移函数，提出了STGARCH模型来衡量波动性.STGARCH模型在两个状态之间，还允许中间状态的平滑移动.STGARCH模型的方差方程在本质上是一个ARMA过程，不能反映波动的长记忆性.

Dacorogna等［8］和Ding等［9］的研究发现，收益率的平方序列与收益率的绝对值序列均存在长期自相关，这意味着波动具有长记忆性.Baillie等［10］提出用FIGARCH模型来刻画波动的长记忆性，并被广泛应用.但是FIGARCH模型的信息冲击曲线是对称的，不能反映波动的非对称性，与事实不符.

Kilic［11］在FIGARCH模型中引入平滑转移函数，提出STFIGARCH模型来同时刻画波动的长记忆性和非对称性，其在FIGARCH模型的条件方差过程中允许非线性动态和非对称性，并引入了平滑转移参数.STFIGARCH模型实际上就是FIGARCH模型和STGARCH模型的综合，可以通过伪极大似然估计（QML）来估计参数.通过模拟仿真发现，当STFIGARCH模型是真实模型时，用FIGARCH模型进行参数估计会产生较大的偏差和标准差.对Canadian Dollar／USA Dollar，Japaneses Yen／USA Dollar，Swiss Francs／USA Dollar和British Pound／USA Dollar这4种汇率，以及S＆P 500和ISE 100股指收益率的实证研究发现，STFIGARCH模型优于FIGARCH模型，非对称性和长记忆性是并存的.

1.2 定价理论

Black等［12］和Merton［13］开创性地提出Black－Scholes期权定价模型，开启了期权定价研究的大门.Black－Scholes模型有许多缺陷，它的一个重要假设是波动率为常数.期权定价模型在波动异方差性上的拓展，根据其所指定的波动率函数的特点，大致可以分为两类：一类是确定波动率模型，将波动率作为标的股票价格序列的函数，如Schroder［14］使用的方差为常数弹性的CEV模型，以及国内学者王植祥等［15］研究期权定价所使用的Lattice方法等；二是随机波动率模型，通过指定描述瞬时资产波动率动态的外生过程建立期权定价模型，如Hull等［16］提出了著名的随机波动性SV模型.但是，实际应用中这些模型的困难之处在于波动是不可观察的.

Duan［17］对风险中性进行了扩展，提出了局部风险中性关系（LRNVR）在风险中性测度和物理测度之间进行变换，并且由此在GARCH模型的框架下构建了欧式期权定价的理论基础.Duan对GARCH期权定价模型进行了大量的实证分析，结果表明GARCH期权定价模型纠正了Black－Scholes模型的定价偏差.Black－Scholes模型是GARCH期权定价模型的同方差资产收益过程的一个特例.

本文首先用STFIGARCH模型对个股波动的长记忆性和非对称性同时进行研究.然后，在Duan期权定价理论框架下，建立了STFIGARCH期权定价模型来研究国内权证定价.

2 GARCH族模型及其期权定价模型

2.1 FIGARCH及其权证定价模型

GARCH过程和IGARCH过程所描述的指数式递减与永久持续性都太具有限制性，严格地按照某一种模型理论来进行研究都没有多大的现实意义.不同于短记忆的GARCH模型和永久记忆的IGARCH模型，Baillie［10］用分形差分算子来代替IGARCH模型中的一阶滞后算子，FIGARCH模型的方差方程为

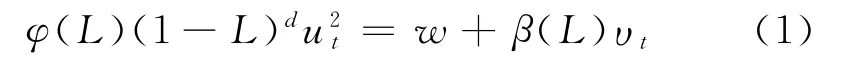
式中，L表示延迟算子；ut代表随机扰动项；d表示分数差分算子；w为常数表示方差与βi为常系数，q与p为常数.φ（L）和β（L）的所有特征根都在单位圆外，式（1）可进一步表示为

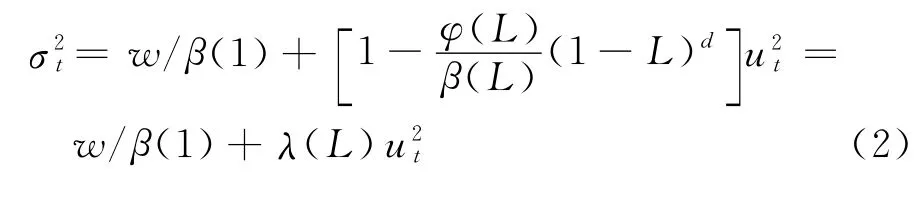
式中，λ（L）＝λ1L＋λ2L2＋…，λ1，λ2…为常系数.

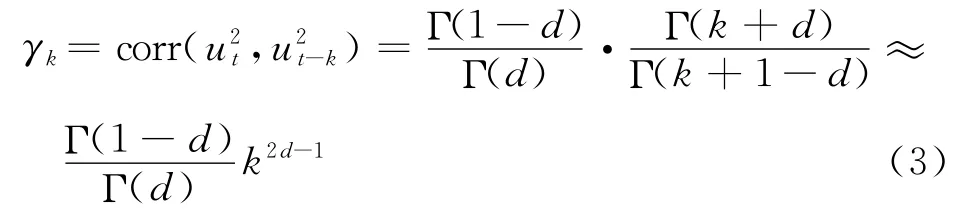
其中，Γ（·）表示Γ函数，k表示两个随机扰动值之间的间隔长度.

可以看出波动率序列以双曲率衰减，呈现模型的长记忆性.FIGARCH模型的局限性在于，其信息冲击曲线是以y轴为中心对称分布的，同样大小的正、负冲击产生同样的波动，没有考虑波动的“杠杆效应”.

根据文献［17］，可利用LRNVR转换成Q测度下的FIGARCH（1，d，1）期权定价模型为

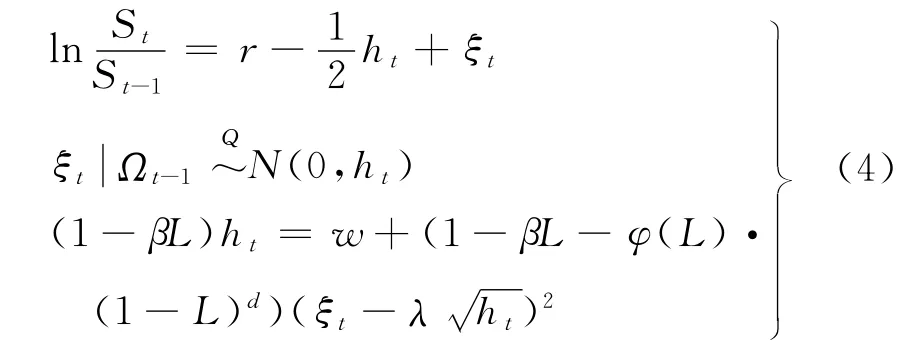
式中，St表示t时期的股票价格；r表示无风险利率；ht表示方差；Ωt－1表示t－1期的信息集合；ξt表示Q测度下服从正态分布的随机变量，且E（ξt）＝0；λ表示单位风险溢价；β为常系数；φ（L）＝1－φL，φ为常系数.

根据该模型，标的价格为

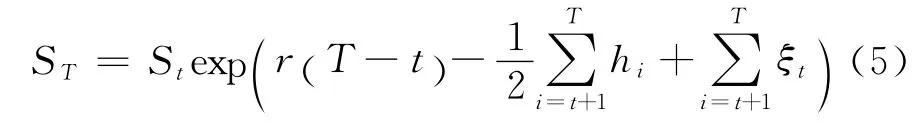
式中，T表示看涨期权的到期时间.

对应的看涨期权价格为

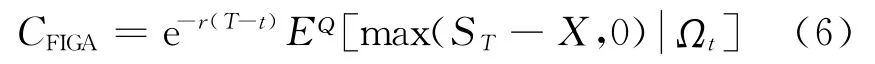
式中，X表示看涨期权的执行价格，EQ（·）表示Q测度下的均值.

式（4）中，GARCH期权定价模型的解析解是不存在的，对该期权价格可以用蒙特卡罗模拟的方法进行计算，得到

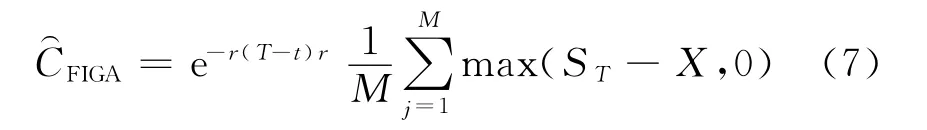
2.2 STGARCH（1，d，1）模型

STGARCH模型是EGARCH模型、GJR模型与AGARCH模型等非对称模型的扩展，有多种设定形式，Hagerud［5］在ARCH项中引入平滑转移，其方差方程为

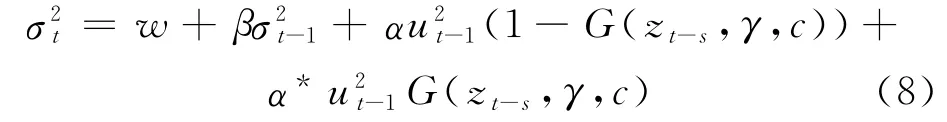
式中，β，α，α＊为系数；G（zt－s，γ，c）代表逻辑转移函数；c表示门限参数；γ表示转移参数；zt－s表示转移变量.G（zt－s，γ，c）＝一般取ut－1.易知，0≤G（·）≤1.γ越大，转移函数G（·）变化越快.当γ→∞时，转移函数在0和1间突变，此时STGARCH模型变成TARCH模型.可见TARCH模型实际上是STGARCH模型在γ→∞时的一个特例.

该模型可以表示成下面的形式，即

对于660MW等级切圆燃烧Π型锅炉和对冲燃烧型锅炉，屏底温度变化对水冷壁、过热器及再热器等受热面的吸热量影响规律基本一致。随着屏底温度的提高，水冷壁吸热量明显降低，而过热器、再热器、省煤器吸热量均有所上升。其中BRL工况下，四角切圆燃烧型锅炉屏底温度每提高10℃，水冷壁吸热量降低1.21%，过热器吸热量提高1.74%，再热器吸热量提高0.63%；对冲燃烧型锅炉屏底温度每提高10℃，水冷壁吸热量降低1.28%，过热器吸热量提高1.20%，再热器吸热量提高0.87%。具体结果见图4。

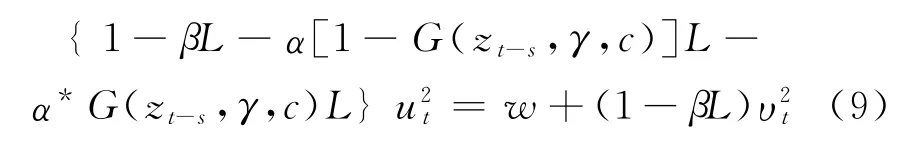
为了同时考虑波动的非对称性和条件方差本身的非对称性，Anderson等［18］在ARCH项和GARCH项中同时引入平滑转移函数，如式（10）所示，即

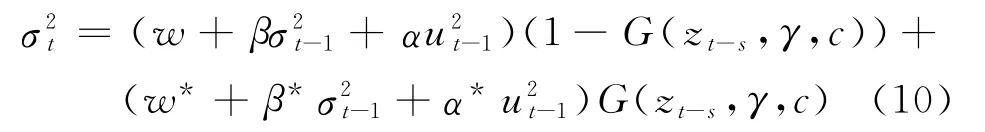
2.3 STFIGARCH及其权证定价模型

本文在FIGARCH（1，d，1）的GARCH和ARCH项同时引入逻辑转移函数，即

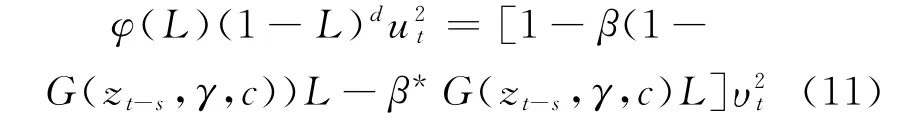
式中，φ（L）＝1－φL，φ为系数；系数β和β＊表示波动动态参数.当zt－s→∞，G（·）→1，此时模型变成波动动态参数为β＊的FIGARCH（1，d，1）模型.当zt－s→－∞，G（·）→0，此时模型变成波动动态参数为β的FIGARCH（1，d，1）模型.若zt－s→c，此时模型变成波动动态参数为的FIGARCH（1，d，1）模型.

式（11）可进一步表示为

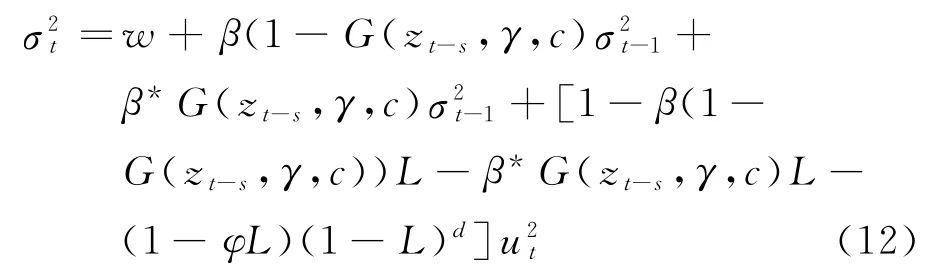
从而得到STFIGARCH模型的ARCH（∞）表示，即

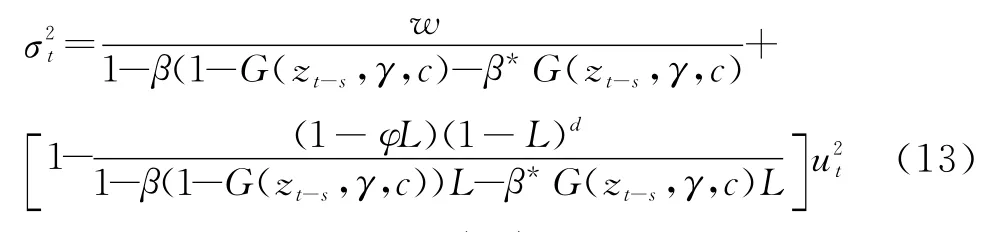
动态参数β，β＊和分别对应该模型的高端状态、低端状态和中间状态.Conrad等［19］得到了该波动过程在某状态下的非负条件.例如，在G（∞，γ，c）→1状态下，该波动过程的非负条件为w＞0，0≤φ≤（1－d）／2，λ＊1＝d＋φ－β＊≥0.注意0≤G（·）≤1，β（1－G）＋β＊G是β和β＊的复合形式，因此可以推导出该条件波动过程的非负条件为w＞0，0≤φ≤（1－d）／2，β≥0，β＊≤d＋φ.

根据文献［17］，在STFI－GARCH模型中可利用LRNVR转换成Q测度下期权定价模型为

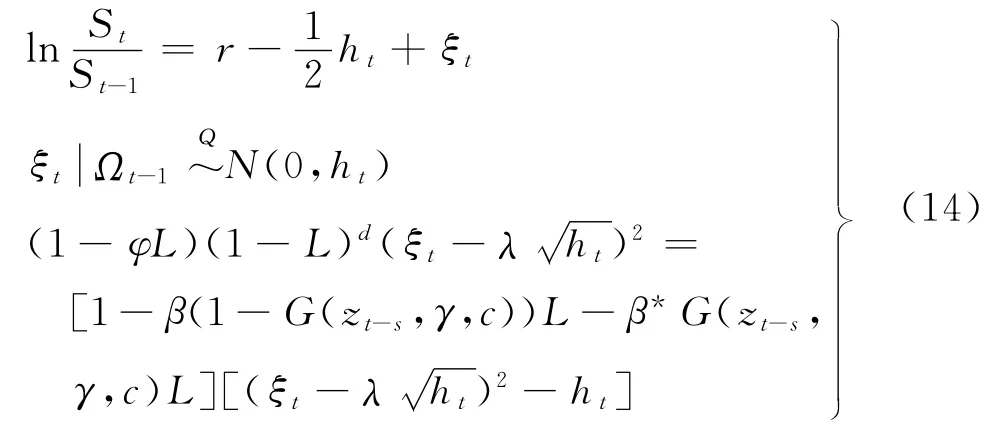
以后的定价步骤与FIGARCH期权定价方法相同，不再重述.

3 研究方法

3.1 STFIGARCH模型的估计

Kilic［11］用伪极大似然估计（QML）方法估计STFIGARCH模型的参数.模型在高斯过程下的对数似然函数为

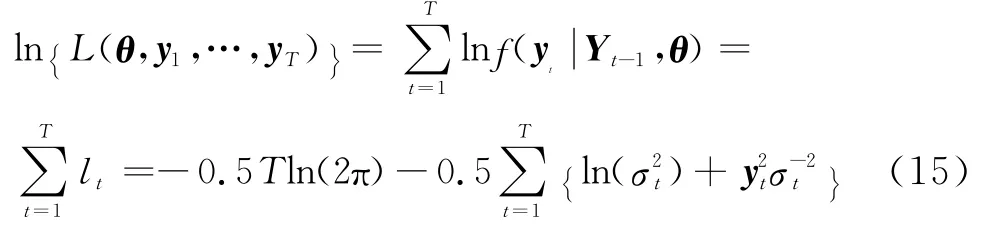
式中，Yt表示观测向量；yt表示预测向量；θ为参数向量；f（·）是概率密度函数；lt表示概率密度函数的对数.式（15）在参数向量θ＝（w，d，φ，β，β，＊γ，c）′处取最大值.

采用Berndt等［20］提出的BHHH算法估计参数ϑ＝（w，d，φ，β，β，＊γ，c，ν），使拟极大似然估计函数（QMLE）最大，其中ν是参数在T分布下的自由度.QMLE估计量的渐进分布如下

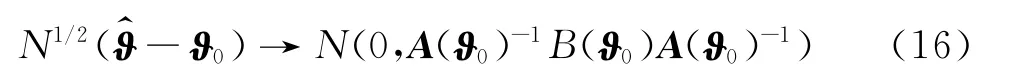
式中，N是样本数；ϑ0是参数的真实值；A（ϑ0）是Hessian矩阵；B（ϑ0）是在ϑ0处的梯度.

3.2 DM检验

Diebold等［21］提出DM检验，对不同预测模型之间的相对预测能力进行比较.DM的假设分述如下：

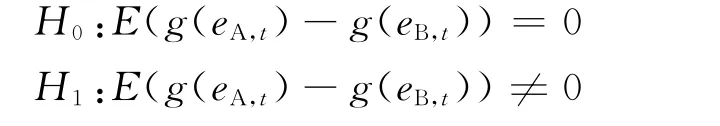
其中，g（eA，t），g（eB，t）分别是模型A和模型B预测误差的函数.令g＝g（eA，t）－g（eB，t），则g被称为损失函数.考虑一条样本路径如果该差分序列是协方差平稳和短记忆的，则可以推导出样本损失差分的渐进分布.构造DM检验统计量为

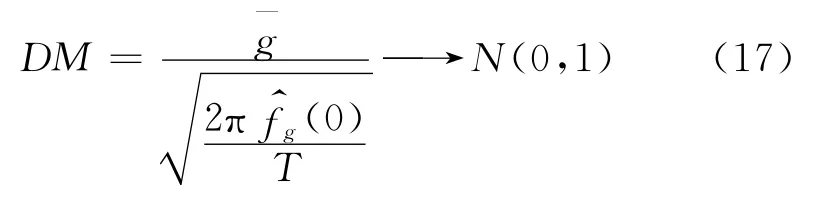
4 实证分析

4.1 源数据与处理

我国权证市场自2005年8月宝钢权证开始上市交易，到2011年8月最后一支权证四川CWB1合约期满，历时5年，期间一度成为世界上交易最为活跃的市场.对这些宝贵的历史数据进行分析，有助于深入理解我国的权证定价机制.由于我国上市权证数量较多，作为分析方法上的一种探索，本文仅选取了长电CWB1与侨城HQC1两支权证，其基本情况如表1所示（见下页）.数据来源于中信证券交易软件.收益序列采用收盘价格的对数差分乘以100求得，即

rt＝100（log（pt）－log（pt－1）） （18）式中，rt代表第t期的收益率；pt代表第t期的股票价格指数.

4.2 平稳性检验和ARCH效应检验

为了消除非平稳性对实证结果的影响，采用ADF方法对指数收益率序列进行平稳性检验.由EVIEWS软件求得P值均为0，因此该收益率序列是平稳的，不存在单位根现象.从图1（见下页）可以直观地看出，收益率的大幅度波动和小幅度波动常常集中在不同的时段，初步判断该收益率序列存在波动的集聚性特征.为了确定波动的集聚性，对收益率进行滞后5阶的ARCH－LM检验得到该值大于在1%的置信水平下，拒绝原假设，表明收益率存在条件异方差现象，适合采用GARCH模型族.

表1 基本信息Tab.1 Basic information

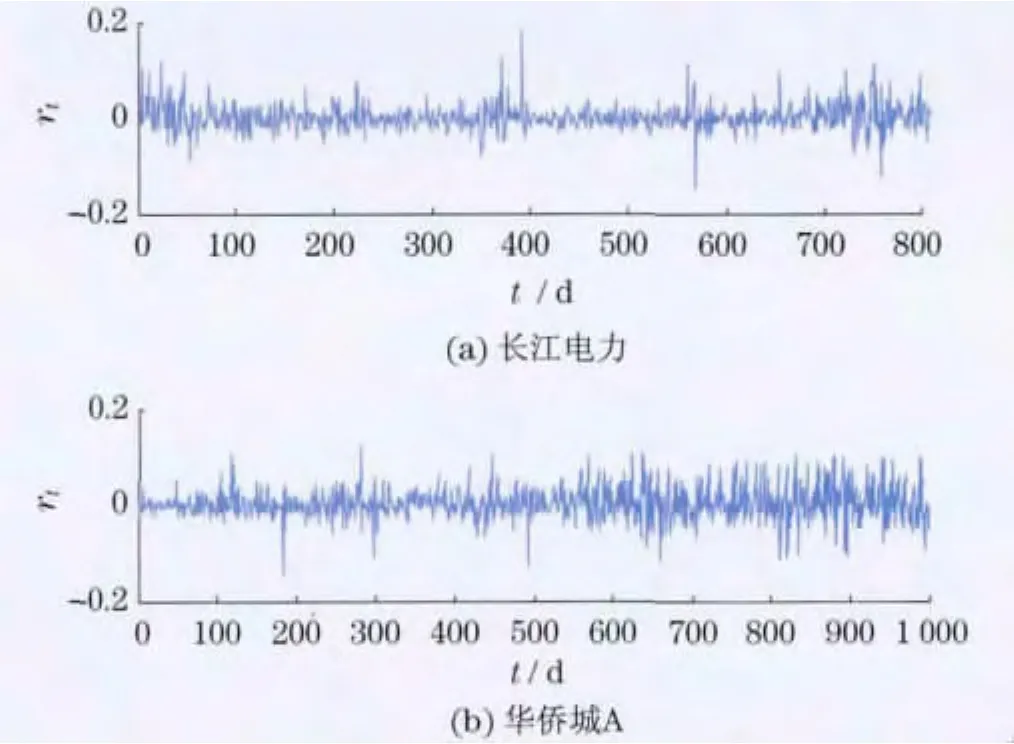
图1 长江电力与华侨城A的收益率序列图Fig.1 Daily return series of Yangtze power and OCT’s

4.3 收益率绝对值的重标极差（R／S）统计量分析与Hurst指数

由图2可知，利用R／S分析法进行检验时，长江电力的Hurst指数为0.697，而华侨城A的Hurst指数为0.69，均大于0.5，这说明波动的替代指标收益率的绝对值序列表现出较强的长记忆性，从而可以认为收益的波动率呈现较强的长记忆性.图中，ln N表示时间序列观测数的对数值，A表示R／S统计量的对数值，R是统计量相关系数.

4.4 参数估计

表2列出了STFIGARCH期权定价模型（STFIGARCH－M）与FIGARCH期权定价模型（FIGARCH－M）的参数值及其标准差.由该表可以发现，无论是FIGARCH模型还是STFIGARCH模型，分整参数d的取值都在0.2～5.8之间，这说明个股波动具有长期记忆性.从最大似然值、AIC准则和BIC准则方面看，STFIGARCH模型均优于FIGARCH模型.与Kilic［11］对S＆P 500和ISE 100的研究结果类似，长江电力的转移参数γ＝2.057 5，深证股指的转移参数γ＝1.986 6，均不太大，这说明个股波动状态变换是较为平滑的.对于长江电力来说，由于β＞β＊，门限参数c＝5.817 1，当ut＞c时代表正的外部冲击（好消息），并且造成较大的股票波动，显示出“反向杠杆效应”.而对于华侨城A，β＜β＊，门限参数c＝2.361 5，当负的外部冲击ut＜c时，造成较大的股票波动，显示出“杠杆效应”.

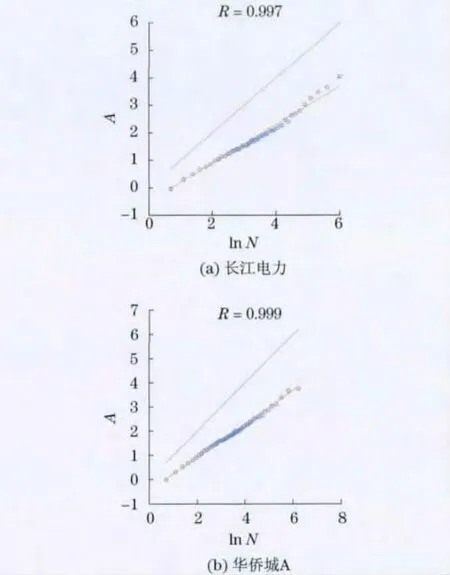
图2 绝对值序列的R／S分析Fig.2 R／Sanalysis of absolute value sequence’s

4.5 期权定价模型结果比较

模型的推导过程中并没有考虑太多现实中的交易成本问题和市场操纵问题，而是适用了B－S期权定价模型的假设条件.分别利用前面的两种定价模型对两支权证自上市之日起存续期间的235和220个价格数据进行预测，然后与市场价格相比较.通过均方误差（MSPE）和平均绝对值误差（MAPE）来检验模型预测波动的精度和能力，分别为：WMSPE＝对 WMSPE与WMAPE进行DM检验，结果见表3.可以看出STFIGARCH－M的预测误差比FIGARCH－M要小，与实际数据更匹配.而统计量分别在5%，15%及12%的统计性水平上不为零，STFIGARCH－M要优于FIGARCH－M模型，因此用STFIGARCH－M来对我国的个股权证进行定价是适宜的.

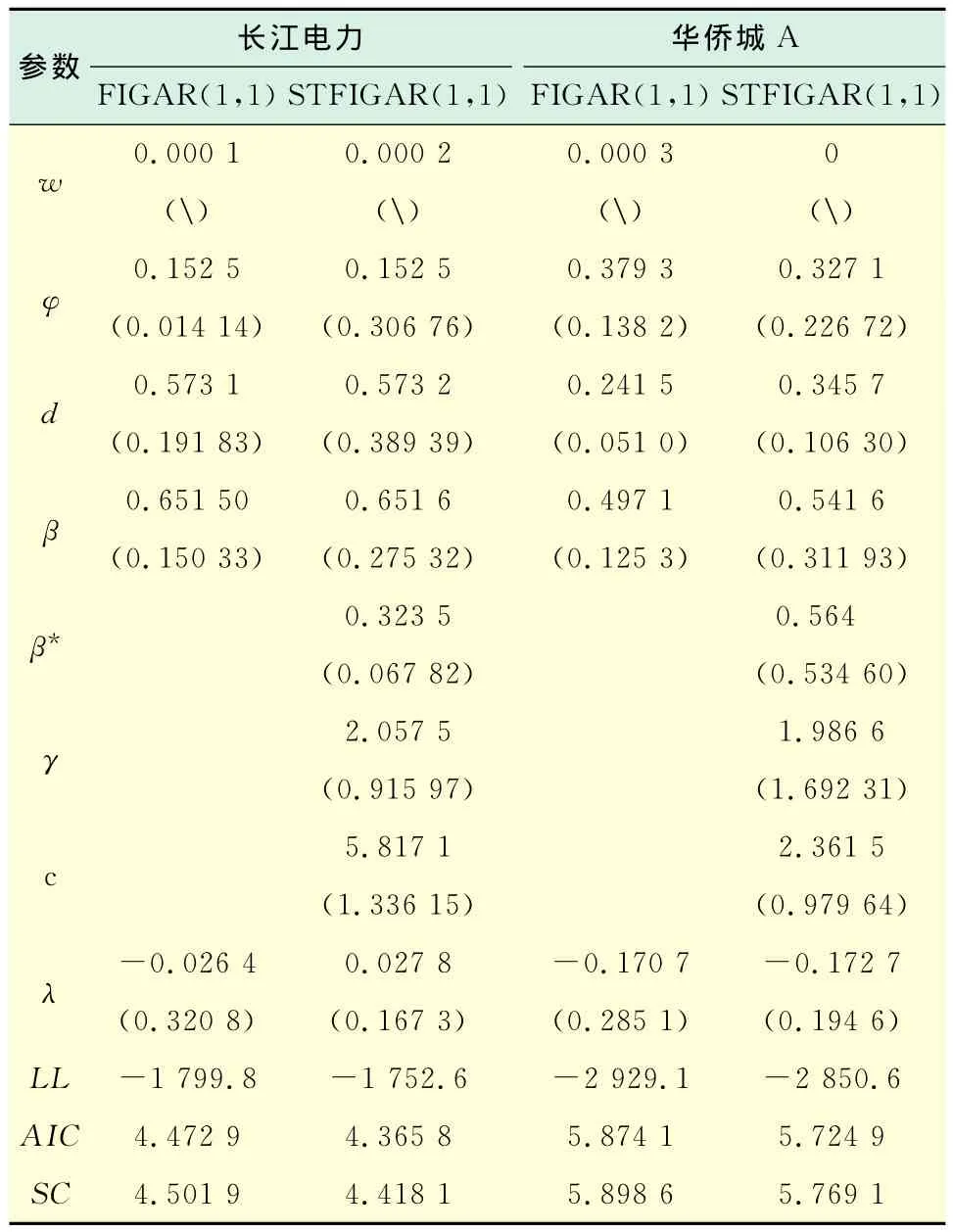
表2 各模型估计结果Tab.2 Models’estimation results

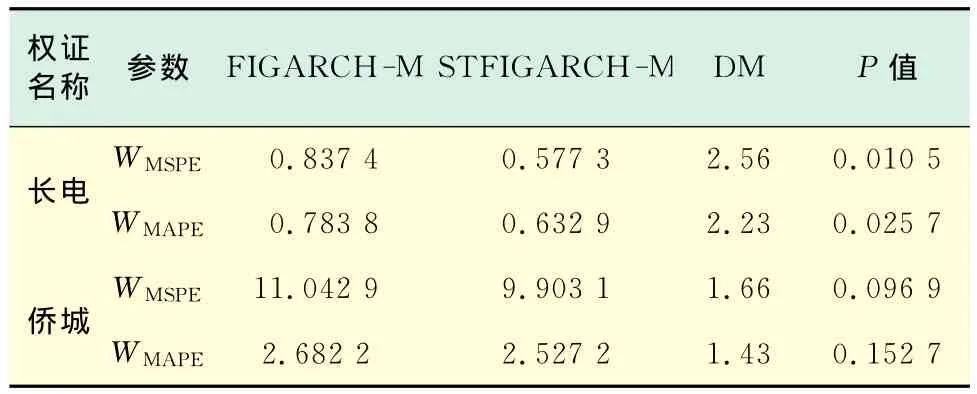
表3 权证预测结果比较Tab.3 Comparison of option pricing estimation results

观察图3，无论是STFIGARCH－M还是FIGARCH－M，权证定价拟合值比权证的实际值要小.这可能是由于我国权证数量有限，供应量太小，创设机制对券商的要求较高，限制了权证的有效供应量，以及不存在卖空机制，投资者无法通过套利操作使权证价格回归合理价位，影响了模型定价的合理性.但是随着行权日越靠近，股票价格的不确定性越来越小，权证价格逐步回归到模型的理论价格.

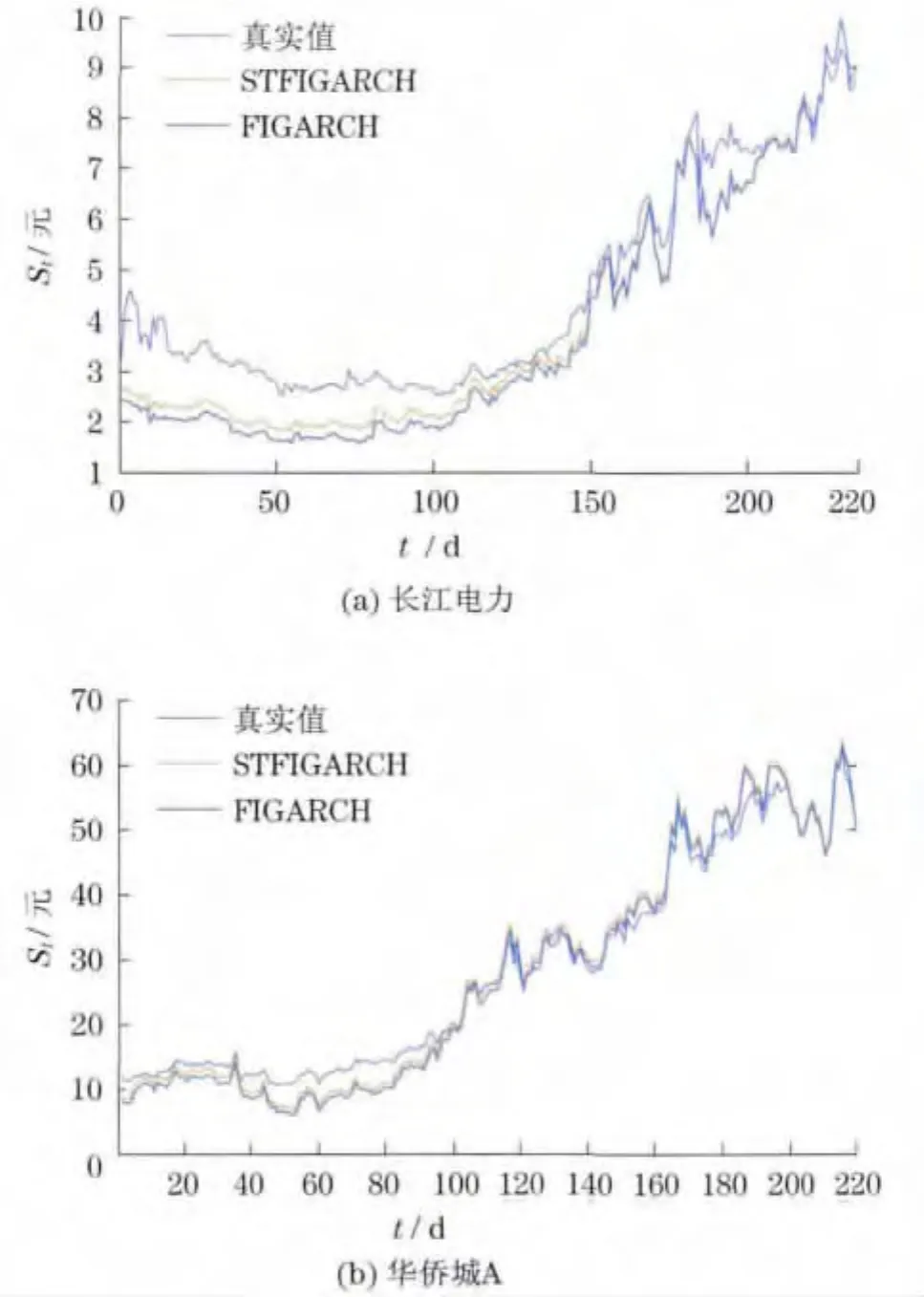
图3 权证定价模型价格比较Fig.3 Pricing comparison with option pricing model

5 结 论

本文探索研究我国权证市场的定价机制，选取了长江电力和华侨城A两支个股进行分析.对收益率序列的R／S检验表明两支个股存在显著的长记忆性效应，这表明基于短记忆的二阶矩建模对波动结构的拟合可能是不充分的.对个股收益率进行长记忆的FIGARCH和STFIGARCH建模，拟合结果显示：STFIGARCH的对数最大似然值较FIGARCH大，而BIC值、AIC值较小，说明STFIGARCH拟合得更好，个股波动的长记忆性和非对称性是共存的.

然后，利用蒙特卡罗模拟进行FIGARCH－M与STFIGARCH－M模型的权证定价，计算出权证的理论价格.实证结果表明，STFIGARCH期权定价模型优于FIGARCH期权定价模型.但是，FIGARCH期权定价模型与STFIGARCH期权定价模型的定价结果在权证发行期均小于真实值，我国权证市场偏向于被高估.随着行权日越靠近，股票价格的不确定性越来越小，权证价格也逐步回归模型的理论价格.

［1］ Nelson D B.Conditional heteroskedasticity in asset returns：a new approach［J］.Econometrica，1991，59（2）：347－470.

［2］ Glosten L R，Jagannathan R，Runkle D E.On the relation between the expected value and the volatility of the nominal excess return on stocks［J］.The Journal of Finance，1993，48（5）：1779－1801.

［3］ Engle R F.Stock volatility and the crash of 87：discussion［J］.Review of Financial Studies，1990，3（1）：103－106.

［4］ Engle R F，Ng V K.Measuring and testing the impact of news on volatility［J］.The Journal of Finance，1993，48（5）：1749－1778.

［5］ Hagerud G E.A new non－linear GARCH model［D］.Stockholm：Stockholm School of Economics，1997.

［6］ Lee J，Degennaro R P.Smooth transition ARCH models：estimation and testing［J］.Review of Quantitative Finance and Accounting，2000，15（1）：5－20.

［7］ Lubrano M.Smooth transition GARCH models：a Bayesian perpective［J］.Rechercheséconomiques de Louvain Economic Review，2001，67（3）：257－287.

［8］ Dacorogna M M，Müller U A，Nagler R J，et al.A geographical model for the daily and weekly seasonal volatility in the foreign exchange market［J］.Journal of International Money and Finance，1993，12（4）：413－438.

［9］ Ding Z X，Granger C W J，Engle R F.A long memory property of stock market returns and a new model［J］.Journal of Empirical Finance，1993，1（1）：83－106.

［10］ Baillie R T，Bollerslev T，Mikkelsen H O.Fractionally integrated generalized autoregressive conditional heteroskedasticity［J］.Journal of Econometrics，1996，74（1）：3－30.

［11］ Kilic R.Long memory and nonlinearity in conditional variances：a smooth transition FIGARCH model［J］.Journal of Empirical Finance，2011，18（2）：368－378.

［12］ Black F，Scholes M.The pricing of options and corporate liabilities［J］.Journal of Political Economy，1973，81（3）：637－654.

［13］ Merton R.Theory of rational option pricing［J］.The Bell Journal of Economics and Management Science，1973，4（1）：141－183.

［14］ Schroder M.Computing the constant elasticity of variance option pricing formula［J］.The Journal of Finance，1989，44（1）：211－219.

［15］ 王植祥，姚俭，杨辉，等.Lattice方法在期权定价中的应用研究［J］.上海理工大学学报，1998，20（1）：22－25.

［16］ Hull J，White A.The pricing of options on assets with stochastic volatilities［J］.The Journal of Finance，1987，42（2）：281－300.

［17］ Duan J C.The GARCH option pricing model［J］.Mathematical Finance，1995，5（1）：13－32.

［18］ Anderson H M，Nam K，Vahid F.Asymmetric nonlinear smooth transition GARCH models［J］.Dynamic Modeling and Econometrics in Economics and Finance，1999，1（1）：191－207.

［19］ Conrad C，Haag B R.Inequality constraints in the fractionally integrated GARCH model［J］.Journal of Financial Econometrics，2006，4（3）：413－449.

［20］ Berndt E K，Hall B H，Hall R E.Estimation and inference in nonlinear structural models［J］.Annals of Economic and Social Measurement，1974，3（4）：653－665.

［21］ Diebold F X，Mariano R S.Comparing predictive accuracy［J］.Journal of Business ＆Economic Statistics，2002，20（1）：134－144.