一类具有非单调传染率的SEIRS时滞传染病模型的全局稳定性

周艳丽， 张卫国

（1.上海理工大学理学院，上海200093；2.上海医疗器械高等专科学校基础教学部，上海200093）

1 模型建立

在传染病动力学模型中，传染率发挥着重要的作用.在以往经典的传染病模型中，通常采用双线性或标准的疾病传染率［1］，使得这些模型的动力学行为比较简单，但结果往往不能客观地反映疾病的传染机理.Capasso［2］研究了1973年发生在Bari的霍乱后，引入了饱和传染率比双线性传染率更符合实际.S（t）表示t时刻未染病但有可能被疾病传染的人数，I（t）表示t时刻已被感染成为病人而且具有传染力的人数，β为接触率，α为常数，α＞0.后来，Liu等在文献［3］中提出了更一般的非线性发生率均为常数，p，q＞0.βIp（t）度量疾病的传染力描述易感者采取措施以抑制传染力.文献［4］研究的是当p＝2，q＝2时，传染病模型的定性分析和分支情况.Xiao和Ruan［5］提出的非线性发生率为更好地体现了g（I（t））与I（t）之间的变化：如疾病初期人们没有意识到疾病的危害性，没有采取有效的措施来阻止疾病的传播，此时，g（I（t））是单调增的；随着染病人数I（t）的不断增加，人们逐渐意识到疾病的危害性，采取一些有效的措施，如隔离或减少与患者的接触，此时，g（I（t））是单调减的.这能更好地反映疾病的传染规律，更符合实际，能为控制疾病传播提供更有效的防御策略.

另一方面，在建立传染病模型时，考虑时滞能较好地反映传染病的潜伏期、免疫期等因素对传染病动力学的影响，因此，对时滞传染病模型的研究受到越来越广泛的重视.近几十年来，已有许多学者研究了大量的时滞传染病动力学模型［6－11］.文献［7］讨论了一类特殊的具有双时滞的SEIRS（易感者、潜伏者、染病者、恢复者）传染病模型，并得到了模型无病平衡点的全局稳定性和地方病平衡点的存在性、唯一性和稳定性的充分条件.Xu等［9］考虑了具有饱和传染率的时滞SEIRS模型，并通过迭代的方法得到了地方病平衡点全局渐近稳定的充分条件.Beretta和Takeuchi［6］研究了具有分布时滞的SIR（易感者、染病者、恢复者）传染病模型的全局稳定性.

本文将研究一类具有非单调感染率的SEIRS时滞传染病模型.设t时刻的总人口N（t）＝S（t）＋E（t）＋I（t）＋R（t），E（t）表示t时刻已经感染疾病，但不具有传染能力的人数；R（t）表示t时刻从染病者类移出的人数.

式中，Λ，μ，β，γ均为正常数；τ，δ为非负常数；Λ表示外界对环境的人口迁入，假设迁入的均为易感者；μ表示人口的自然死亡率；δ表示免疫丧失率，δ＞0，意味着恢复者具有暂时免疫力，δ＝0，意味着恢复者具有永久免疫力；γ表示染病者的恢复率；τ为时滞（即疾病潜伏期）.

运用微分动力系统的方法，研究潜伏期和非单调发生率对系统（1）动力学行为的影响.

2 平衡点和基本再生数

根据实际的生物意义，系统（1）将基于以下初始条件：

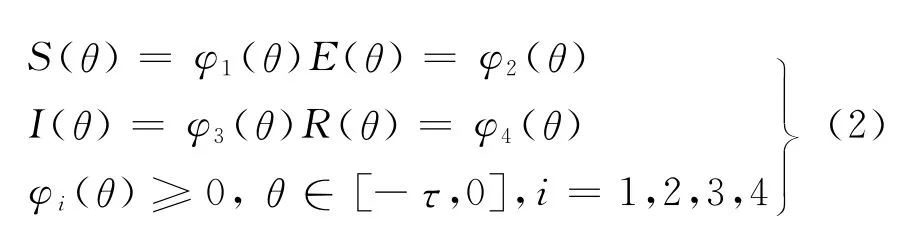
式中，初始函数φ1（θ），φ2（θ），φ3（θ），φ4（θ）是Banach空间C＝C（［－τ，0］，ℝ4＋）上的连续函数.

定义系统（1）的可行域

关于可行域的不变性可得命题1.

命题1 可行域Γ是系统（1）的正不变集，即若满足初始条件式（2），则当t≥0时，系统（1）所有的解（S（t），E（t），I（t），R（t））都在可行域Γ内.

证明 若（S（θ），E（θ），I（θ），R（θ））∈Γ（θ∈［－τ，0］），则由文献［12］可知，系统（1）的解局部存在且唯一.注意到，若对－τ≤θ≤0，有I（θ）≡0，则当t≥0时，I（t）＝0是系统（1）的第3个方程的解.由系统（1）可知，在曲面S（t）＝0上，若（0，E（t），I（t），R（t））∈Γ，则成立.同理，可以证得对所有的t≥0，有E（t）≥0，I（t）≥0，R（t）≥0.由系统（1）的第4个方程可知，在曲面R（t）＝0上，若（S（t），E（t），I（t），0）∈Γ，则在曲面E（t）＝0上，若（S（t），0，I（t），R（t））∈Γ，则在曲面I（t）＝0上，若（S（t），E（t），0，R（t））∈Γ，则0.所以，若（S（θ），E（θ），I（θ），R（θ））∈Γ，则系统（1）的解不可能从边界S（t）＝0，E（t）＝0，I（t）＝0，R（t）＝0跑出区域Γ.

将系统（1）的各式相加，得到

其中

因此

所以，（S（t），E（t），I（t），R（t））∈Γ，则Γ是系统（1）的正不变集.

定义系统（1）的基本再生数为

定理1 当R0≤1时，则系统（1）在Γ内有唯一的无病平衡点当R0＞1时，则系统（1）在Γ内，除了无病平衡点P0还存在一个正平衡点P＊（S＊，E＊，I＊，R＊）（地方病平衡点），其中

经计算，I＊由下面的式子决定：

方程（5）当且仅当R0＞1时，有唯一的正实根（地方病平衡点）.

3 各类平衡点的局部稳定性

利用类似于文献［8－9］的方法，证明系统（1）的无病平衡点和地方病平衡点的局部稳定性.

显然，方程（6）有3个负实根，λ1＝－μ，λ2＝－μ，λ3＝－（μ＋δ）.方程（6）其余的根由方程

决定.令

若R0＞1，则无病平衡点P0是不稳定的，因为

因此，方程（7）至少有1个正实根，所以，若R0＞1，则无病平衡点P0是不稳定的.

若R0＜1，则方程（7）的所有的根均具有负实部（Reλ＜0）；反之，有Reλ≥0成立.由方程（7）得

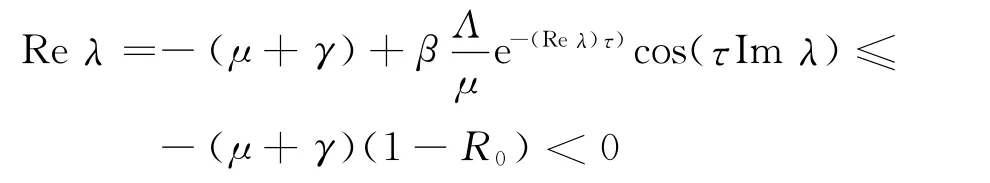
所以，当R0＜1时，无病平衡点P0是局部渐近稳定的.

当R0＝1时，无病平衡点P0是退化的，因为，若R0＝1，对于方程（6）有唯一的零根和3个负根.

由以上分析得到定理2.

定理2 a.若R0＜1，则系统（1）的无病平衡点P0是局部渐近稳定的；

b.若R0＝1，则系统（1）的无病平衡点P0是退化的；

c.若R0＞1，则系统（1）的无病平衡点P0是不稳定的.

计算系统（1）在地方病平衡点P＊（S＊，E＊，I＊，R＊）处的线性化系统，并得到相应的特征方程

显然，有1个根，λ＝－μ，其余的根由下面的式子决定：

其中

当τ＝0时，方程（8）变为

如果R0＞1，通过计算可得

显然

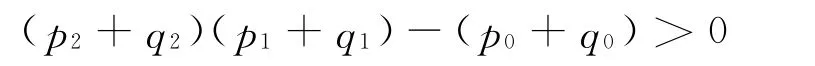
因此，方程（9）当R0＞1和τ＝0时，所有的根均具有负实部.

如果iω（ω＞0）是方程（9）的解，代入方程（9）并分离实部和虚部，得到如下结果：

对以上两式两端平方后加在一起并整理，可得

通过计算可得

同理，可得

通过以上分析可知，当R0＞1时，式（10）不存在正实根，所以，当R0＞1时，系统（1）的地方病平衡点存在且局部渐近稳定.

通过以上分析得到定理3.

定理3 若R0＞1，则系统（1）的地方病平衡点P＊（S＊，E＊，I＊，R＊）是局部渐近稳定的.

4 无病平衡点的全局稳定性

定理4 若R0≤1，则系统（1）的无病平衡点P0是全局渐近稳定的.

证明 考虑Lyapunov泛函

当R0≤1时，且等号成立的充分必要条件是R0＝1或I＝0.当I＝0时，有当t→＋∞时，有E→0和R→0，故使得的最大正向不变集为（S，E，I，R），由李亚普诺夫－拉塞尔不变集定理［13］可知，系统（1）的无病平衡点在Γ内是全局渐近稳定的.

5 地方病平衡点的全局稳定性

系统（1）的第1，3，4式中不含E（t），所以，只需要研究下面的子系统：

令u1＝S（t）－S＊，u2＝I（t）－I＊，u3＝R（t）－R＊，并在（0，0，0）处线性化，得到

其中

定理5 若R0＞1，同时满足mi＞0（i＝1，2，3），则系统（11）的地方病平衡点P～＊（S＊，I＊，R＊）是全局渐近稳定的，其中

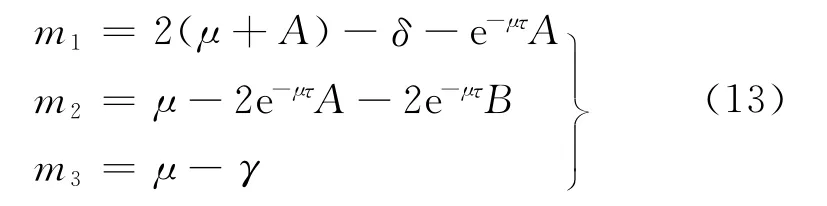
证明 令

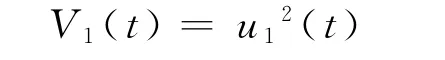
计算V1沿系统（12）的导数为

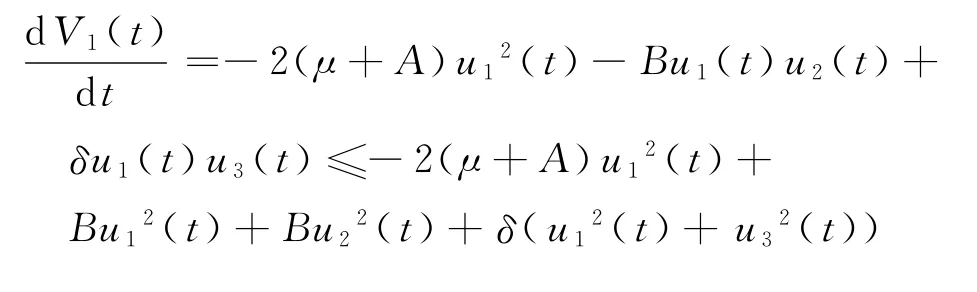
令

计算V2沿系统（12）的导数为

令

计算V3沿系统（12）的导数为

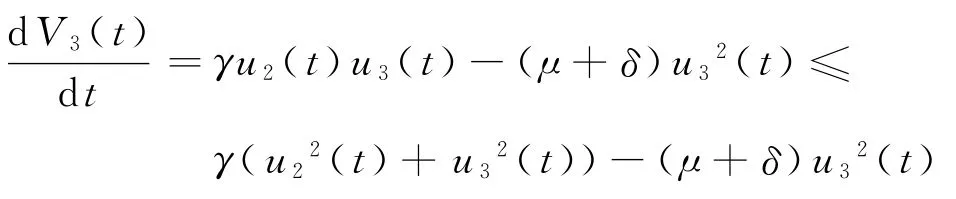
令

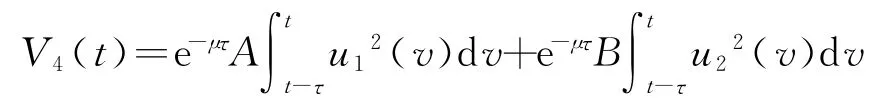
计算V4沿系统（12）的导数为

定义Lyapunov泛函

其正定性显然，V沿系统（12）的导数为

其中

由mi＞0（i＝1，2，3），得负定，所以，地方病平衡点P＊（S＊，E＊，I＊，R＊）在Γ内是全局渐近稳定的.

6 讨论和数值模拟

通过数值仿真验证本文所得主要结论.在图1中，取Λ＝2，β＝0.1，α＝6，γ＝0.5，μ＝0.2，δ＝0.2，τ＝2，使得R0＝0.957 6＜1，满足定理4的条件.从图1中可以看到，系统（1）的无病平衡点P0（10，0，0，0）是全局渐近稳定的，这与定理4的结论吻合.在图2中，取Λ＝5，β＝0.8，α＝6，γ＝0.2，μ＝0.4，δ＝0.2，τ＝2，使得R0＝7.488＞1，且m1＝ 0.785 3，m2＝5.424 8，m3＝0.2，满足定理5.从图2中可以看到，系统（1）的地方病平衡点P＊（10.477，1.724，0.937 8，0.312 6）是全局渐近稳定的，这与定理5的结论一致.

图1 系统（1）无病平衡点的渐近行为Fig.1 Asymptotic behavior of the disease－free equilibrium in system（1）

图2 系统（1）地方病平衡点的渐近行为Fig.2 Asymptotic behavior of the endemic equilibrium in system（1）

本文的疾病传染率虽然与文献［10］的疾病传染率不同，但有着相类似的结论.本文结合实际情况，考虑到疾病初期对人们的影响较小，人们没有采取积极的措施来控制疾病的传播，这时疾病的传染力会增大.随着疾病的不断传播，人们逐渐意识到疾病的危害性，人们会采取有效的措施减少与染病者的接触，同时社会上的有关卫生部门也会对染病者采取隔离等一些措施以减少疾病的传播，这时疾病的传染力会变小，这样的传染率更符合实际，体现了人们的心理作用和社会行为.本文的基本再生数与文献［10］相同，同时得到，当R0≤1时，无病平衡点是全局渐近稳定的；当R0＞1时，地方病平衡点全局稳定性的充分条件.

文献［10］主要研究的是传染率具有饱和性且带有时滞的SEIRS模型.

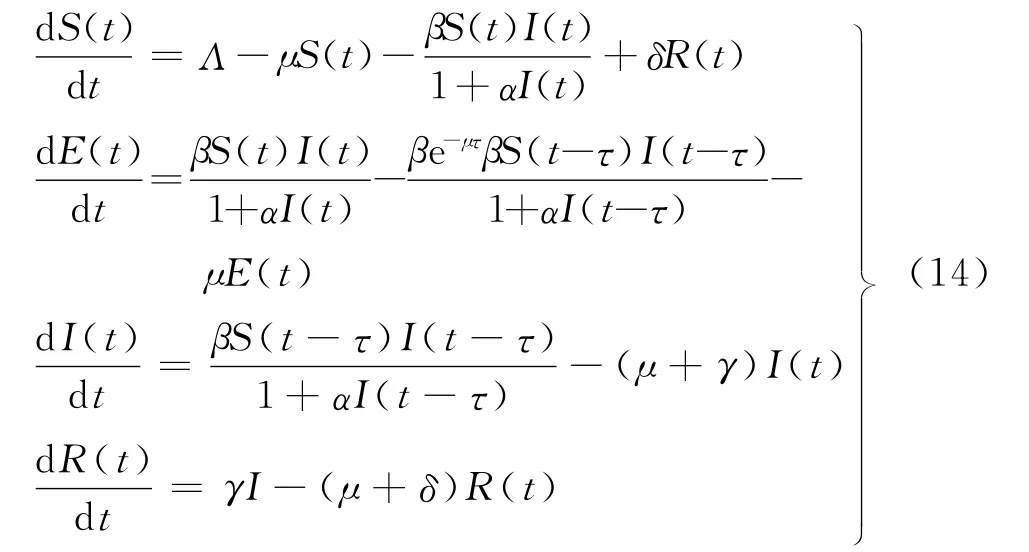
［1］ 周艳丽，王贺桥.具有隔离和接种策略的传染病模型稳定性分析［J］.上海理工大学学报，2010，32（3）：249－252.

［2］ Capasso V.A generalization of the Kermack－Mckendrick deterministic epidemic model［J］.Mathematical Biosciences，1978，42（1／2）：41－61.

［3］ Liu W M，Levin S A，Iwasa Y.Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models［J］.J Math Biol，1986，23（2）：187－204.

［4］ Ruan S G，Wang W D.Dynamical behavior of anepidemic model with a nonlinear incidence rate［J］.Journal of Differential Equations，2003，188（1）：135－163.

［5］ Xiao D M，Ruan S G.Global analysis of an epidemic model with nonmonotone incidence rate［J］.Math Biosci，2007，208（2）：419－429.

［6］ Beretta E，Takeuchi Y.Global stability of an SIR epidemic model with time delays［J］.Math Biol，1995，33（3）：250－260.

［7］ Cooke K L，Van den Driessche P.Analysis of an SEIRS epidemic model with two delays［J］.J Math Biolo，1996，35（2）：240－260.

［8］ Beretta E，Hara T，Ma W B，et al.Global asymptotic stability of an SIR epidemic model with distributed time delay［J］.Nonlinear Analysis，2001，47（6）：4107－4115.

［9］ Xu R，Ma Z E.Global stability of an SIR epidemic model with nonlinear incidence rate and time delay［J］.Nonlinear Analysis：Real World Applications，2009，10（5）：3175－3189.

［10］ Xu R，Ma Z E.Global stability of a delayed SEIRS epidemic model with saturation incidence rate［J］.Nonlinear Dynamics，2010，61（1／2）：229－239.

［11］ Gao S J，Chen L S，Teng Z D.Impulsive vaccination of an SEIRS model with time delay and varying total population size［J］.Bulletion of Mathematical Biology，2007，69（2）：731－745.

［12］ Hale J K，Lunel S M V.Introduction to functional differential equations［M］.New York：Springer－Verlag，1993.

［13］ Miller R K，Michel A N.Ordinary differential equations［M］.New York：Academic Press，1982.