沙坑回灌补给地下水的数值模拟分析
2014-03-22田竹君肖长来田浩然
杜 超,田竹君,肖长来,田浩然
(1.松辽流域水资源保护局松辽水环境科学研究所,吉林 长春 130021;2.吉林大学 环境与资源学院,吉林 长春 130021)
沙坑回灌补给地下水的数值模拟分析
杜 超1,田竹君1,肖长来2,田浩然1
(1.松辽流域水资源保护局松辽水环境科学研究所,吉林 长春 130021;2.吉林大学 环境与资源学院,吉林 长春 130021)
文章对一般性的沙坑回灌补给地下水模型进行了概化,建立了水文地质概念模型和数值模型,采用 GMS 软件对沙坑回灌补给地下水的效果进行了模拟分析。结果表明,沙坑回灌补给地下水的累计渗漏量与时间呈线性关系;渗漏速率在渗漏初期大于渗漏后期,经过一定时间后趋于稳定;单个沙坑回灌补给引起地下水明显上升的范围较小,效果有限。
沙坑回灌;地下水;渗漏量;渗漏速率;数值模拟
由于社会经济的不断发展,在中国的很多地区尤其是北方地区,地表水资源已经远远不能满足人类的生活生产需要,许多城市供水与农业灌溉用水走上了盲目大规模开采地下水这条道路,造成了地下水资源不断减少,地下水位持续下降等不良后果。随着观念的转变,人们对地下水资源的保护越来越重视,很多地方都开始着手建立地下水回灌工程。在实施工程前,应对回灌可能产生的效果进行可行性分析,而数值模拟技术正是进行分析的有效手段。下面采用数值模拟技术对沙坑回灌补给地下水的效果进行分析,讨论回灌过程中沙坑渗漏量、渗漏率、影响半径随时间的变化关系,得出了沙坑回灌补给地下水的一般性规律。
1 沙坑回灌模型
为了探讨沙坑回灌补给地下水的一般性规律,对沙坑回灌模型做如图 1 的概化,矩形沙坑深 10 m,BC=ED=10 m,CD=20 m。沙坑底水平,沙坑水位为 3 m,未渗漏前地下水初始水位距沙坑底部 2.5m。将土层分为两种方案来分别模拟:一种是土层为层状土,上层为粗砂,下层为砂砾石;另一种是土层为均质砂砾石。对渗透系数取不同的值来模拟不同时刻沙坑内水流的渗流情况。由于是做一般性探讨,所选参数相对较大。
方案一:上部为粗砂,渗透系数 K=50 m/d;下部为砂砾石层,渗透系数 K=150m/d,给水度 μ=0.3。
方案二:土层均质砂砾卵石渗透系数 K=200 m/d,给水度 μ=0.3。

图1 沙坑回灌模型示意图
2 水文地质概念模型
2.1 含水层概化
对方案一,含水层渗透性在垂向上呈层状分布,概化为非均质各向同性潜水含水层;对方案二,含水层渗透性在垂向上不发生变化,概化为均质各向同性潜水含水层。
2.2 水力特征概化
沙坑回灌模型中地下水流各要素随时间发生变化,概化为非稳定流;地下水流主要在平面方向上流动,潜水面随时间发生动态变化,概化为潜水二维流。
2.3 边界条件概化
1)侧向边界。由于沙坑中水流不断补给地下水,将很快影响到距沙坑较近的地方。若边界条件选择离沙坑过近,则边界的水头及流量会很快发生变化,从而影响模型模拟结果。因此,边界采用远离沙坑中心的零流量边界,边界距沙坑中心 5 km。
2)垂向边界。潜水面为潜水含水层的上部水量交换边界,潜水含水层底板为隔水边界。当沙坑中的水流与地下水取得水力联系后,由于沙坑中水头固定不变,此时即为潜水含水层的定水头边界。
3 数学模型的建立与求解
3.1 数学模型的建立
均质、潜水二维地下水非稳定流数学模型如下:
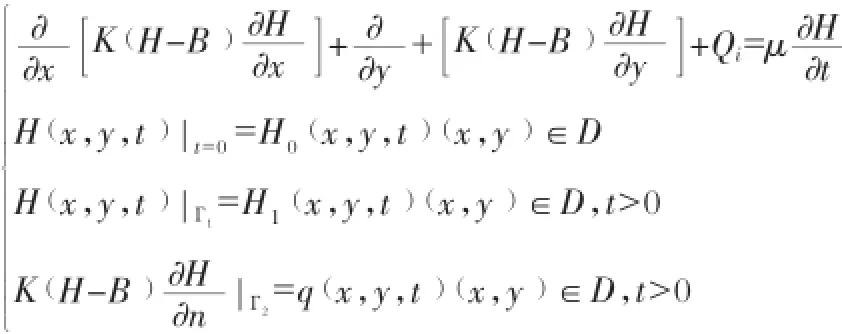
式中:K——潜水含水层渗透系数,m/d;μ——潜水含水层给水度;H——潜水水位,m;B——潜水含水层底板标高,m;Qi——源汇项补给/排泄强度,m/d;H0——初始潜水水位,m;H1——研究区一类边界处潜水水位,m;q——研究区二类边界单宽流量,m3/(d·m);x,y——坐标,m;D——计算区范围;Г1,Г2——研究区一类、二类边界。
3.2 模型离散
1)空间离散。以沙坑定水头矩形边界 4 个顶点为基准点,对沙坑定水头边界附近水力梯度变化较大的区域进行网格加密。将计算区剖分为 174 列、174 行,共 30 276 个网格单元。最小网格单元长 0.25 m,宽 0.25 m,面积 0.625 m2。网格偏离系数取 1.1。
2)时间离散。模拟期为 3 年,以观测长时间条件下沙坑回灌补给地下水的稳定情况。模拟初期地下水水位变化较快,变幅较大,故模型运行的前 5 d以1 d为一个应力期,1 h 为一个时间步长;第 6~30 d 以 1 d 为一个应力期,4 h 为一个时间步长;第 31~365 d 以 1 d 为一个时间步长;第 366~1 095 d 以 5 d 为一个时间步长。
3.3 初始水位
数学模型在沙坑水与地下水取得水力联系并使坑底地层达到饱和后才适用。显然沙坑开始注水后会迅速渗透至潜水面并达到饱和。在计算时,假设沙坑中水位由无水状态突然上升到设计水位,坑底地层达到饱和,给定边值条件,作为稳定流问题可以求得它的解 H x,( )y ,把这个解近似作为沙坑充水后非稳定流问题的初值 H0x,( )y。
4 模型预测
采用GMS软件进行求解,假设模拟期除沙坑定水头补给外,无其它源汇项,以查看沙坑回灌地下水的效果。
4.1 方案一
1)累计渗漏量的变化。累计渗漏量与时间成线性相关的关系,相关系数 R2=0.997 8。累计渗漏量与时间的相关曲线见图 2(a)。
2)渗漏速率的变化。沙坑渗漏初期地下水流场变化快于渗漏后期,渗漏速率亦是初期大于后期。渗漏开始天内尤其是渗漏最初 1天是渗漏速率最快的阶段,随后渗漏速率逐步递减,1年后渗漏速率减缓的速率趋于稳定。渗漏速率与时间关系曲线见图 3(a)。
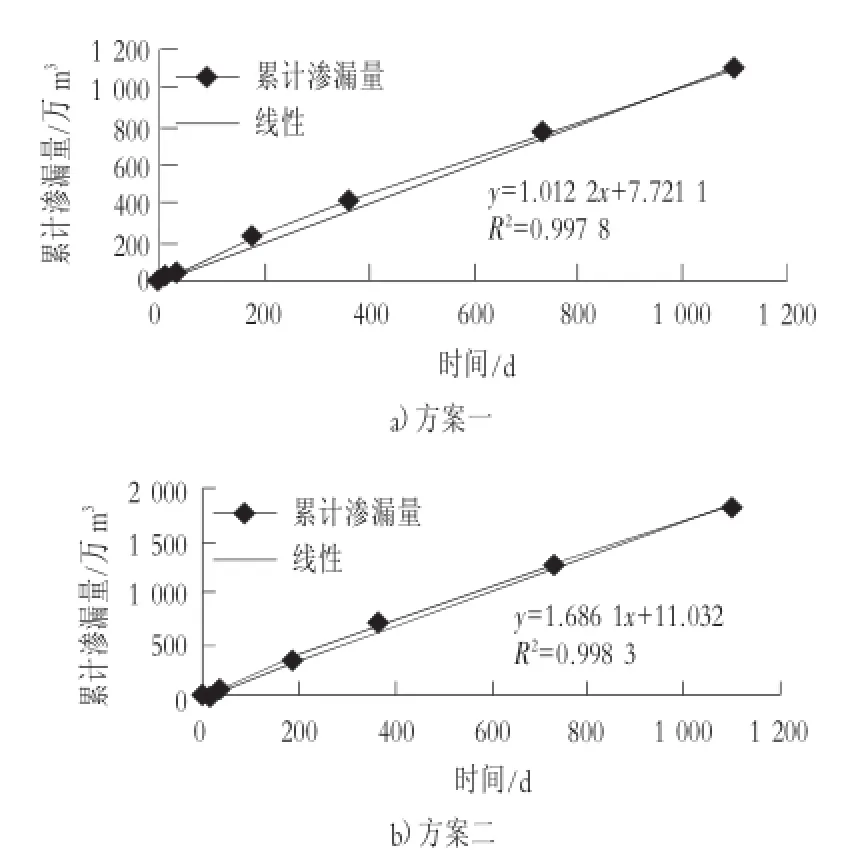
图2 累计渗漏量与时间相关关系曲线图

图3 渗漏速率与时间关系曲线图
3)影响半径的变化。3 年内沙坑渗漏的最大影响半径可达 1 800 m,其中水位升幅超过 0.5 m 的影响半径可达1 200 m,而沙坑渗漏引起的水位升幅超过 2m 的范围有限,年变化不大。不同时刻沙坑渗漏补给地下水流场剖面见图 4(a)。
4.2 方案二
1)累计渗漏量的变化。累计渗漏量与时间成线性相关的关系,相关系数 R2=0.998 3。累计渗漏量与时间的相关曲线见图 2(b)。
2)渗漏速率的变化。沙坑渗漏初期地下水流场变化快于渗漏后期,渗漏速率亦是初期大于后期。渗漏开始 3 d 内尤其是渗漏最初 1天是渗漏速率最快的阶段,随后渗漏速率逐步递减,1年后渗漏速率减缓的速率趋于稳定。渗漏速率与时间关系曲线见图 3(b)。
3)影响半径的变化。3 年内沙坑渗漏的最大影响半径可达 2 400 m,其中水位升幅超过 0.5 m 的影响半径可达1 630m,而沙坑渗漏引起的水位升幅超过 2 m 的范围有限,年变化不大。不同时刻沙坑渗漏补给地下水流场剖面见图 4(b)。

图4 不同时刻沙坑渗漏补给地下水流场剖面图
5 结语
无论渗透系数大小如何,沙坑渗漏初期地下水流场变化均快于渗漏后期,渗漏速率亦是渗漏初期大于渗漏后期。渗透系数大时影响半径大,渗透系数小时影响半径小。沙坑回灌补给地下水的累计渗漏量与时间呈线性关系;渗漏速率在渗漏初期大于渗漏后期,在一定时间后趋于稳定。
单个沙坑回灌补给引起地下水明显上升的范围较小,效果有限。若要使大面积地下水水位回升,需在漏斗区内均匀布置多个沙坑进行回灌才能有较好效果。
[1]石学厚.珍惜人类的共有资源,建设地下水回灌工程[J].北京水利,2001(1):21.
[2]王新娟,谢振华,周训,等.北京西郊地区大口井人工回灌的模拟研究[J].水文地质工程地质,2005(1):70-72 ,84.
[3]赵卫,王滨,陈杰等.三江平原人工回灌地下水的有效途径与方法[J]. 水利科技与经济,2004,10(2):74-75.
[4]李坷凌, 宋丽红. 安阳市地下水回灌的可行性分析[J].地下水,2004,26(2):109-111.
[5]薛禹群,吴吉春.地下水数值模拟在我国[J].水文地质工程地质,1997(4):21-24.
[6]薛禹群,吴吉春.面临 21 世纪的中国地下水模拟问题[J].水文地质工程地质,1999(5):1-3.
[7]李俊亭.地下水流数值模拟[M].北京:地质出版社,1992.

表1 汛期污染物综合衰减系数计算表
表2 非汛期污染物综合衰减系数计算表
[收稿日期]2013-08-09
TV211.1+3
B
1002-0624(2014)01-0035-03
2013-07-30
