基于交通特征的空域建模方法及扇区仿真分析
2014-03-21陈阳舟张德夫宋卓希
毕 虹 陈阳舟 张德夫 宋卓希
0 引 言
空域动态扇区划分的目的是在保证管制安全和飞行安全的基础上,均衡分配各扇区管制员的工作负荷,使其工作负荷在合理的阈值之内。要达到动态扇区划分的目标,关键是对空中交通情况的准确分析。针对不同的空中交通情况采用与之相适应的扇区划分,保证管制的安全和效率。空中交通情况通常可以反映在交通特征上,交通特征包括空域静态结构特征和空域动态交通特征。空域静态结构特征包括扇区划分、航路分布、关键点数量(机场、航路点、交叉点)、地形、导航辅助设备等等。空域动态交通特征随时间变化而变化,包括空域内航空器数量、航空器混合情况、天气、航空器间间隔、航空器速度和交通流量限制等。
空域模型作为扇区优化划分方法的基础,直接影响扇区划分结果。目前,扇区划分研究中提出了不同的建模方法。按照空域模型的建立过程中空域特征信息的利用情况,可以将空域模型分为表1中所示的三类。
文献[1]、[2]采用正六边形离散空域。文献[1]中指出了在确定网格大小时应考虑的相关因素。采用网格模型虽然建模简便,但是,模型不能反映空域交通的信息,只是作为统计管制员工作负荷和扇区划分的基本单元,难以满足扇区划分安全性的要求。同时,基于网格模型生成的扇区边界呈锯齿状,在划分后需要进行边界平滑的处理[2]。文献[3]基于Voronoi图模型划分扇区。先利用优化算法优化中心点位置,然后利用Voronoi图算法直接生成扇区边界。通过这种方法生成的扇区边界可能和航路(或关键点)重合,不能保证满足扇区约束条件。

表1 空域模型Tab.1 Airspace model
基于加权图模型的研究通常在建立加权图模型时采用关键点合并[4]或关键点周围添加保护区[5]等方法,保证了划分后的扇区满足扇区约束条件。由于空中交通是实时变化的复杂系统,空域结构难以反映空域中复杂的交通情况和不同时刻的交通特征。
航迹模型采用飞机飞行的轨迹作为建模信息[6],轨迹包括飞行的起始终止位置及其对应的时间信息。这类研究虽然可以体现某段时间内的空域交通实时变化情况,但是,舍弃空域中如关键点位置等这些固定不变的特征,难以判断约束条件是否得到满足。
综合分析现有的空域模型,发现其均存在不足之处[7]。普遍问题在于空中交通信息利用的不够充分,
尤其是空域的动态交通特征信息不全。本文提出一种新的空域建模方法,首先利用空域静态结构特征建立空域复杂网络模型,然后,基于空域复杂性评估空域某段时间内的动态交通特征,并建立空域加权复杂网络模型。以关键点及其周围航路作为聚类对象,应用基于空域加权复杂网络的 K-Means聚类算法,将空域分为若干区域,每个区域中包含的关键点及其周围航路具有相似的交通特征,而不同区域之间的交通特征差异较大,如图1所示。
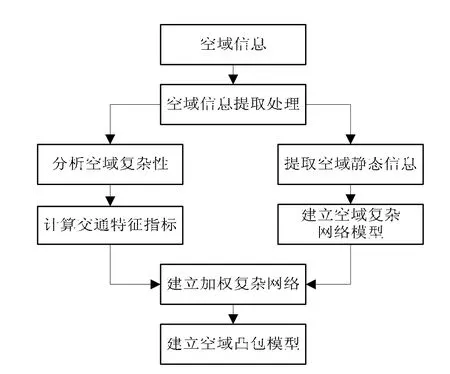
图1 基于交通特征的空域建模流程Fig.1 Modeling process of the airspace based on the traffic features
在实际的空域管理中,应尽可能减少扇区划分导致的扇区边界变化,这样便于管制员工作交接和对管制空域工作的熟悉。目前,多数研究都基于点和线(加权图模型、航迹模型)或者很小的格子(网格模型)划分扇区,均可能导致不同时段的扇区边界变化过大。如果基于区域改变扇区结构,不同时间段内的扇区边界在空间上具有一定的连续性。本文提出的建模方法将空域按照交通特点分为若干区域,扇区的划分和合并将在这些区域间进行。这在一定程度上保证扇区划分结构和人员配备的连续性,划分后的新扇区满足方便管制移交和扇区空域相对集中的要求。除此之外,由于管制员工作负荷中的协作负荷的大小与扇区划分直接相关的,本文通过聚类将部分交通繁忙的航路包含在聚类后的区域中,避免扇区边界穿过这些航路,减少扇区边界的协作负荷,从而减少整个空域范围内的管制员工作负荷,达到增加空域容量的目的。
1 基于空域交通特征建立空域模型
由于空中交通特征的概念比较抽象,并且涉及复杂多变的空域动态特征,在研究中借助空域复杂性的概念,辨识出与空中交通特征相关的空域交通复杂性因素。基于众多的空域交通复杂性因素,采用主成分分析法,选取其中的五个主要因素,并将这五个主要因素简化为两个反映空域交通特征的指标。然后,基于空域交通特征指标建立了空域的加权复杂网络模型。最后,在该空域模型的基础上将空域聚类,形成空域凸胞模型。
1.1 基于空域复杂性提取空中交通特征的主要指标
航路、管制扇区、航空器、飞行员、通信设备及管制员管制过程的相互作用构成了动态空中交通系统。这些因素在不同时刻、不同交通模式下相互影响,构成了空中交通的复杂性[17]。空域复杂性概念最初的提出是为了研究管制员工作负荷。基于空域复杂性的工作负荷评估试图从使管制员产生工作负荷的根本原因——交通特征及其变化情况着手,建立各种复杂的空域管制因素与工作负荷之间的统计学关系。所以,空域复杂性在某种程度上形容了空域交通特征的各项因素及其复杂变化。
空域复杂性研究中最根本的问题是对复杂性因素的完整系统辨识,目前已归纳出数十种与空域复杂性相关的因素[8]。如交通密度、爬升/下降的航空器数、高度变化量、航空器速度方差、航行角度方差、交通混合情况、风、路径最近点分布、汇聚角度、航空器意图认知水平等。对这些空域复杂性因素进行分析,通过主成分分析选出能代表空域 85% 特征的五个指标:(1)航空器平均通过时间;(2)总的冲突数量;(3)航空器平均速度;(4)航空器数量;(5)爬升的航空器比例。定义了两个主成分,分别为“密度因子”(主成分一)和“飞行态势因子”(主成分二)。通过主成分分析法可知两个空域交通特征指标的得分函数如下:
密度因子=0.247平均通过时间 + 0.348总冲突次数 - 0.383平均速度 - 0.011爬升航空器比例 + 0.413航空器数量
飞行态势因子=-0.685平均通过时间-0.024总冲突次数+0.141平均速度+0.465爬升航空器比例-0.153航空器数量
1.2 基于加权复杂网络特征的 K-Means聚类算法的空域建模
空域交通系统符合复杂网络的特点[9],将其视为复杂网络,不同的空域有不同的节点分布特点和密集程度,研究空域的范围及其交通特征也直接影响复杂网络的规模。加权复杂网络能够比较完整地表达复杂网络的结构,且可以结合空域的动态特征和静态特征。本节将基于加权复杂网络的聚类方法论述空域凸胞模型的建立方法。
1.2.1 基于加权复杂网络特征的K- means 聚类算法
本文中的聚类算法利用了加权复杂网络中节点加权度、加权聚集系数等概念。节点的加权度反映了该节点与其它节点的连接强度。节点的加权聚集系数体现了此节点局部范围内的相互连接密度和强度。由节点的加权度和加权聚集系数得到加权网络的综合特征值,则基于加权复杂网络特征的K- means 聚类算法(WCNFC)步骤如下[10]:
Step1 根据原始数据集计算相似度, 得到相似度矩阵。
Step2 根据相似度矩阵建立加权复杂网络。首先以数据为节点, 相似度作为数据之间连边的权值表示数据之间的连接强度。
Step3 计算各个节点的加权复杂网络综合特征值。
Step4 对各节点的加权复杂网络综合特征值进行排序, 形成由大到小的队列。
Step5 从队列中依次选取K个加权网络综合特征值高, 且与已被选作初始聚类中心的节点之间没有连边的节点作为初始聚类中心。
Step6 以所选的 K个节点作为初始聚类中心,采用 K-means 算法,根据相似度矩阵对数据集进行划分迭代,形成聚类。
1.2.2 建立空域凸胞模型
首先,基于静态空域结构建立空域复杂网络模型。具体方法如下:将关键点作为网络节点,如果关键点(航路点、航路交叉点和机场)之间有飞机飞行(或航路连接),则认为对应的两个节点间存在联系,以边相连。图2为基于北京管制区静态空域结构建立的空域复杂网络模型(图中所示的航路为北京管制区主要航路,包含80%以上的交通信息)。
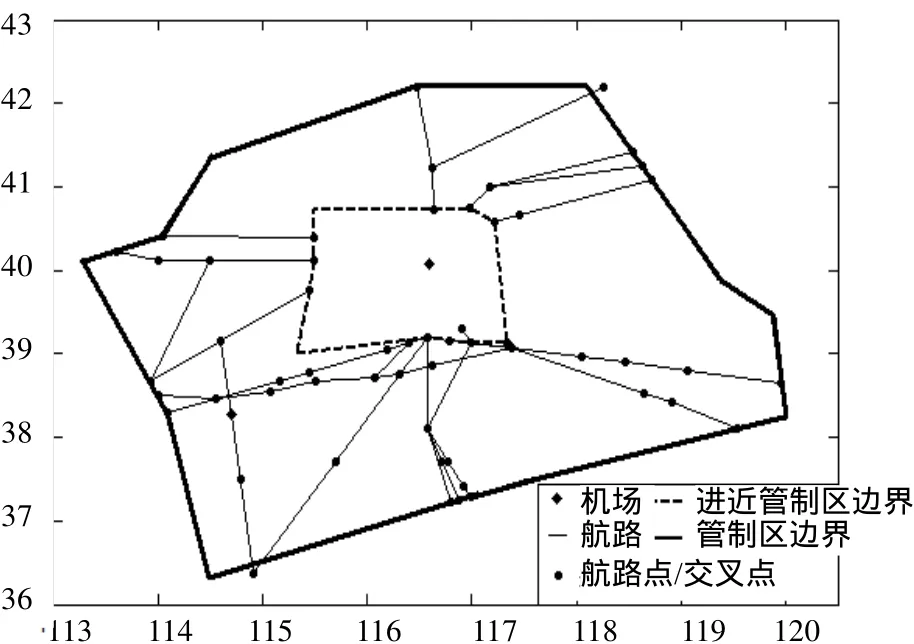
图2 北京管制区网络Fig.2 Network of Beijing management district
结合 1.1节中复杂性主要指标的主成分分析结果,采用向量空间法将每个关键点周围的交通特征表示成复杂性因子向量。因此,对于第i个关键点,有复杂性向量 di=(t1i, t2i)。其中, t1i表示主成分一在关键点i区域的值, t2i表示主成分二在关键点i区域的值。计算相关联节点之间的相似度,以相似度作为网络边的权值,建立加权复杂网络,采用WCNFC算法对关键点进行聚类,得到空域的凸胞模型。
由于空域内交通分布的不确定性,聚类结果可能不满足扇区连通性约束。故改进算法,在复杂性因子向量中增加关键点的位置信息,即 di=(t1i, t2i, xi, yi),其中, xi和 yi表示关键点i的坐标。这样可以在一定程度上保证聚类后凸胞内关键点的连通性。对于聚类后仍不满足连通性的类,直接按照连通性分为新的若干类,得到最终的空域凸胞模型(图3)。由于K-means聚类算法自有的特性,聚类结果在几何上具有凸性。为了满足扇区最小距离约束和最短时间约束,凸胞的边界和关键点之间的距离大于最小安全距离。

图3 凸胞模型Fig.3 The conver hull model
2 基于空域凸胞模型的扇区划分有效性分析
本文以北京管制区的实际交通数据作为算法应用对象,采用文献[11]中的基于遗传算法的扇区划分方法对北京管制区进行扇区划分。以管制区内航班历史飞行计划为主要数据来源,用2012年某天(天气晴朗)的实际交通数据对航班历史飞行计划进行必要的修正,得到空域的动态交通数据。结合空域静态结构,可以得到关键点位置数据库、航路网络拓扑结构数据库、航班航迹数据库、航段飞行动作数据库等,这些数据库将作为扇区划分算法的数据基础。
2.1 空域建模方法有效性分析
北京管制区的交通高峰期为13:00至17:00。图4反映了北京管制区的交通流量在高峰期的平均分布情况,航迹的密集程度与航段的交通繁忙情况成正比。对比图2可以看出,通过聚类算法生成的凸胞内包含一部分交通繁忙的航段。
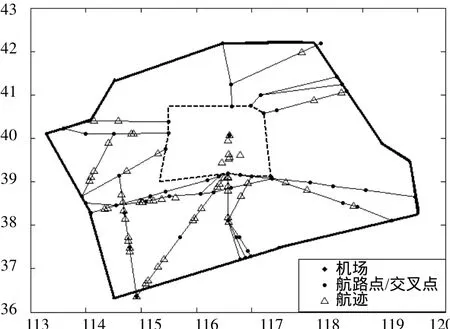
图4 北京管制区交通高峰期交通分布示意Fig.4 Traffic distribution in the traffic peak of Beijing traffic management district
由于加权图模型在扇区划分研究中的应用最为普遍,本文将基于相同的扇区优化划分算法,分别基于凸胞模型和加权图模型对北京管制区进行扇区划分。图5展示了不同的两个时间段内基于两种空域模型的扇区划分结果(每个时段的北京管制区均具有相同的扇区数)。表2为不同时段扇区划分所对应的管制员工作负荷。
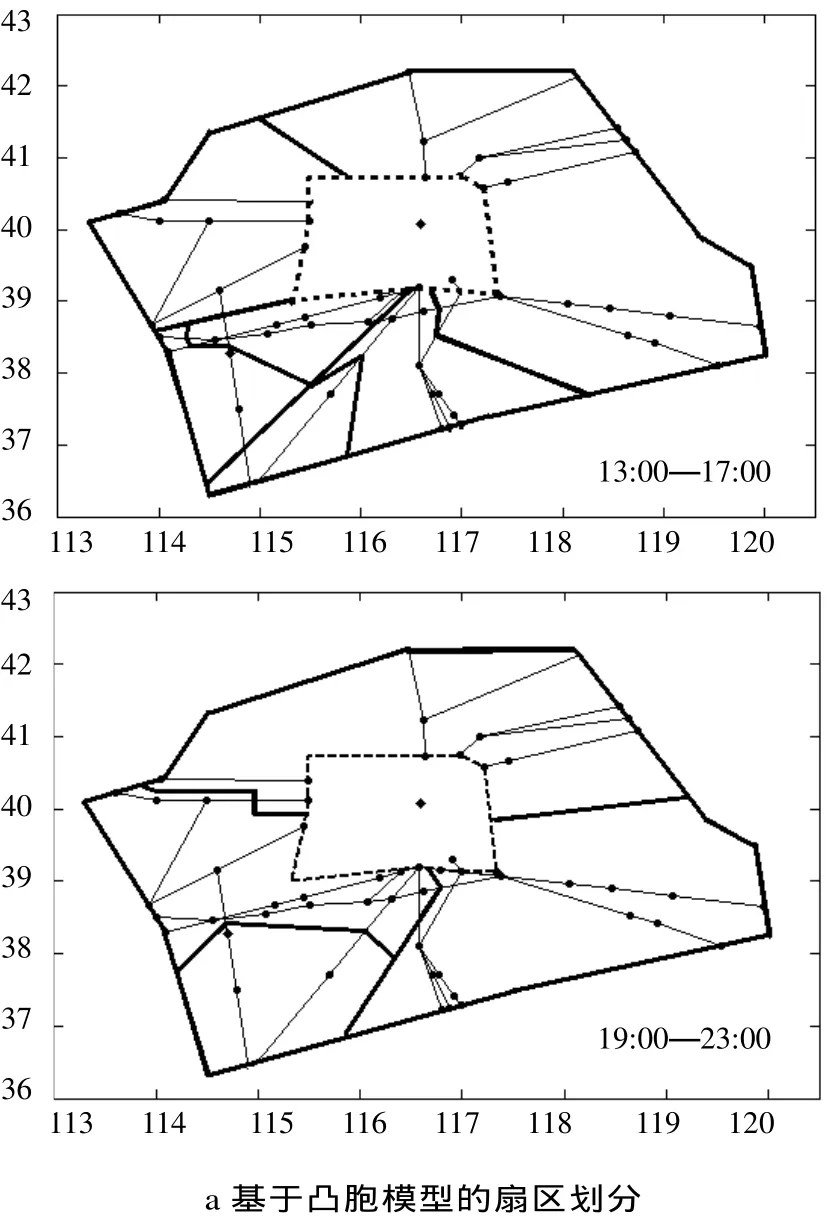
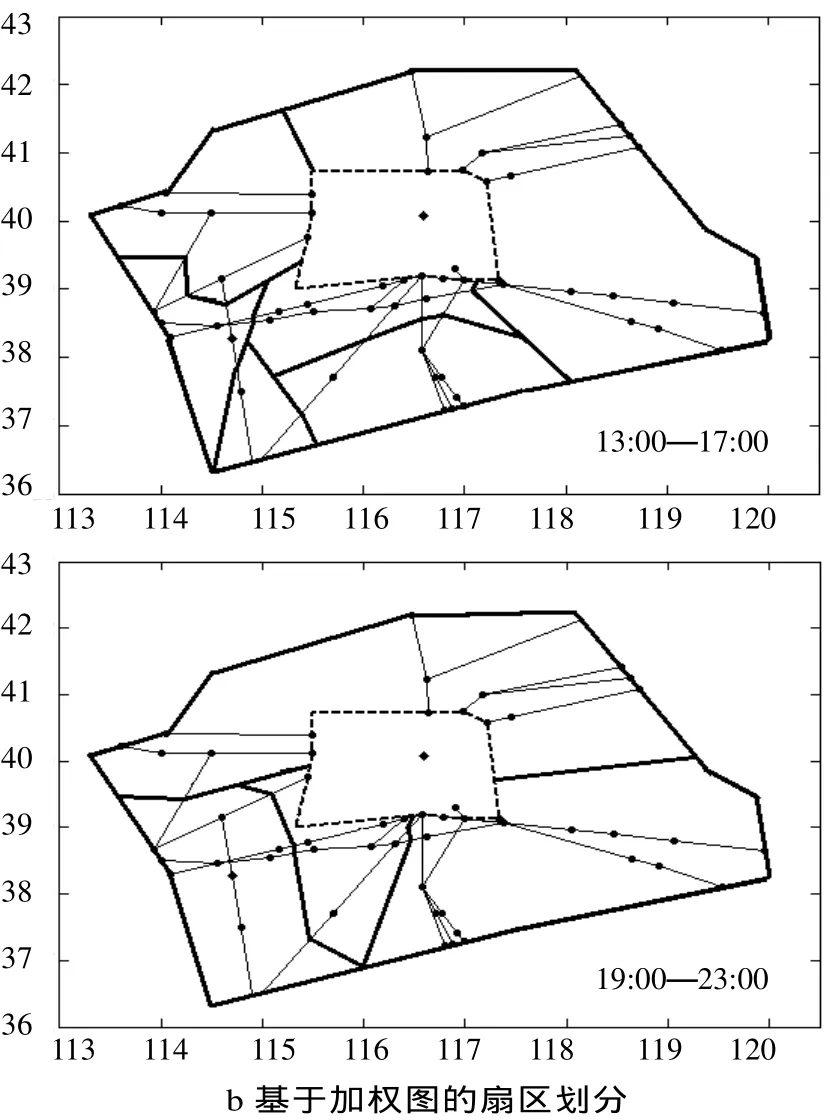
图5 扇区划分结果Fig.5 Sectorization results

表2 管制员工作负荷Tab.2 Work loads of the management staff
以高峰期(13:00—19:00)为例,图5a中的协作负荷小于图5b中的协作负荷,这使得总负荷减少了15.7%。并且,图5a中扇区的划分在空间上有一定的连续性,较图5b的变动小。这样利于管制员工作的交接和对管制空域的熟悉,在一定程度上保证扇区结构的稳定性。
2.2 基于凸胞模型扇区优化方法的有效性分析
本文将通过扇区的安全性、工作负荷的均衡性等几个方面分析扇区划分结果。在扇区划分满足扇区约束条件的基础上,用以下几个指标量化性能评价标准:
(1)扇区数目 扇区数目应与空域交通情况的变化相适应,尽可能少的扇区数目有利于减少管制成本。
(2)停留时间 航班在扇区内有较长的停留时间,不仅有利于管制安全,还将减少穿越扇区边界的次数,提高飞行效率。
(3)扇区内的航班数 扇区内包含较多的航班有利于增加扇区空域的使用率。但是,由于扇区内的管制员工作负荷与其所管制的航班数直接相关,考虑到管制安全,各扇区包含的航班数不应超过管制的安全上限M。通常认为管制员所承受的管制负荷应小于其最大所能承受工作负荷的80%。假设每个扇区的管制员最多可同时管制10架飞机,则本文中M取8。
为了基于扇区数目评价扇区划分的安全性和均衡性,我们借助统计分析中概率和数学期望的概念,引入每分钟扇区内包含k架飞机的概率P(k)、平均飞机数k和扇区安全概率C,具体定义如下:

式中,T表示扇区划分周期内的累计分钟数; Nsector表示该周期内的扇区数目; k = 1 ,2,…, n 表示任意采样时刻某个扇区内包含的飞机数;n表示每分钟各扇区中包含最多的飞机数; Nairplane表示在整个周期内各扇区包含k架飞机数的次数;则

其中,k反映了扇区内飞机数目的平均值;C表示扇区划分周期内安全管制时间的百分比,理想值为100%,即整个扇区划分周期内每个扇区所包含的飞机数都小于管制安全的上限M。
2.2.1 交通高峰期扇区划分算法有效性分析
扇区划分的主要目标是各扇区管制员工作负荷均衡。若以10分钟为统计周期,分别计算北京管制区交通高峰期(13:00—19:00)每个周期内各扇区的平均飞机数,得到该时间段内平均飞机数的变化情况:每个扇区的平均飞机数大致围绕5波动,曲线基本包络在4.5—5.5的范围内。这说明划分的扇区负荷基本均衡,在高峰期内各扇区的飞机数目基本保持在小范围内波动,交通量比较稳定。
高峰期内北京管制区各扇区的平均停留时间和最短停留时间如图6所示。每个扇区的平均停留时间基本都在十分钟以上,最短停留时间保证在5 min左右,则北京管制区的平均停留时间为17.013 min,最短停留时间为 3 min。扇区划分可保证管制员有足够的时间管制进入扇区的飞机。
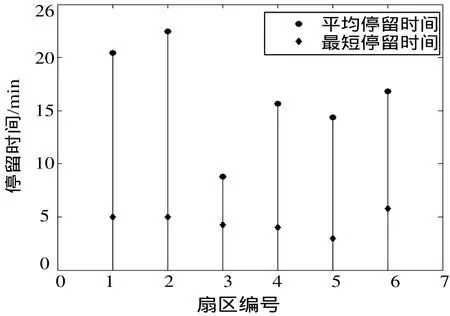
图6 停留时间Fig.6 Stay time
取一分钟为采样时间,图7表示了在高峰期内每个扇区内曾出现过的最大飞机数。扇区2和扇区6曾出现过 9架飞机,超越管制安全上限的时间分别为3 min和7 min。在高峰期内,T = 2 40,Nsector= 6 ,N =8,P( k)的概率分布曲线如图8所示。在该时间段内,每个采样时刻每个扇区平均包含5架飞机(k= 4 .982)。C= 9 9.51%,表示超过99%以上的时间,各扇区内包含的飞机数满足安全要求,划分的扇区可以保证管制的安全性。

图7 扇区内最大的飞机数Fig.7 The biggest plane number in the sector

图8 飞机数的概率分布(划分扇区)Fig.8 Probability distribution in the divided sectors
图9 为北京管制区当前的扇区划分结构。基于相同的交通数据计算当前扇区划分高峰期的 P ( k)的概率分布曲线(图10),其中 T = 2 40,Nsector=2,N = 1 4。平均飞机数k= 3 .58和扇区安全概率 C = 9 8.27%。划分后的扇区明显在安全性上高于当前的扇区,并且扇区的利用率更高更均衡。
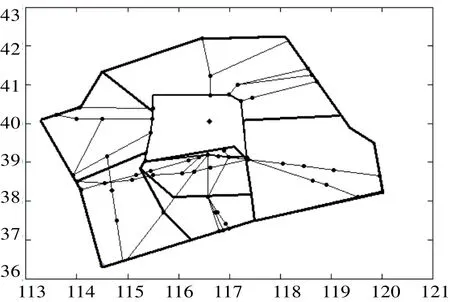
图9 北京管制区当前扇区划分Fig.9 Current sectorization of Beijing management district
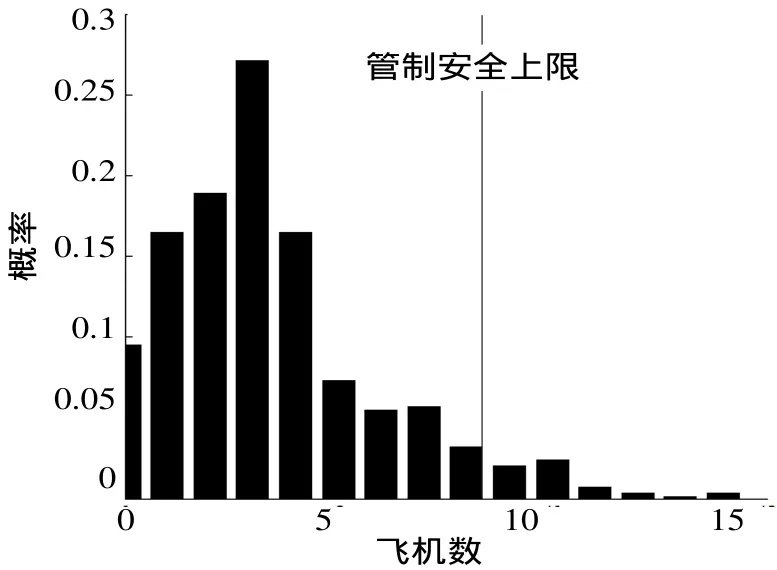
图10 飞机数的概率分布(当前扇区)Fig.10 Plane probabitity distribution in the current sectors
2.2.2 全天扇区划分有效性分析
空域扇区动态划分目的是根据管制区内交通情况的变化情况,确定不同的扇区划分结构,在确保管制安全的基础上,优化配置管制资源,增加空域容量。图11为基于北京管制区全天交通流量的扇区数目变化情况。在保证扇区内的管制负荷在安全阈值之内的前提下,扇区数目随着交通流量的变化而变化,符合交通的变化趋势。

图11 北京管制区交通流量及扇区数目变化曲线Fig.11 Curve between the traffic flow and the sector number change within Beijing traffic management district
基于本文中的扇区划分方法对北京管制区的不同时间段进行扇区划分。以 30 min为周期,计算每个周期内的平均飞机数k,图 12为划分扇区全天的平均飞机数变化曲线。在空域较为繁忙的时间段,扇区的平均飞机数围绕5波动,说明划分后的扇区负荷较为均衡,且扇区数目的变化与交通流量的变化相符,优化了扇区管制人员的资源优化配置。全天安全概率 C = 9 9.63%,超过99%以上的时间管制区内各扇区出现的最大飞机数不大于安全管制上限。作为对比,图13描述了在当前扇区划分下全天的平均飞机数变化曲线,全天的扇区飞机平均数波动明显(即使在扇区数目相同的高峰期内,也比同时间段划分后的扇区平均飞机数曲线波动明显)。由于扇区数目固定,虽然可以保证更多时间内管制的安全性,但是,在交通流量较少的情况下,每个扇区内管制员的管制负荷过小,浪费了管制资源。

图12 平均飞机数变化曲线(划分扇区)Fig.12 Change curve of the mean plane number in the divided sectors
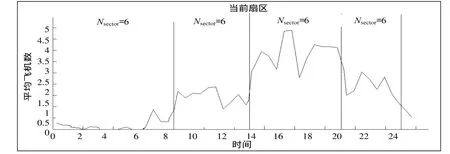
图13 平均飞机数变化曲线(当前扇区)Fig.13 Change curve of the mean plane number in the current sectors
3 结束语
本文利用空域复杂性评估空域交通的特征,并通过密度和飞行态势两个指标综合量化交通特征。在此基础上基于加权复杂网络特征的K- means 聚类算法建立空域凸胞模型,将具有相似交通特征的空域区域聚为一类。基于该模型得到的扇区划分不仅在一定程度上保证了扇区切换后扇区结构在空间上的连续性,还减少了由于扇区划分而产生的管制员交接负荷,提高了管制效率。本文中将提出的方法应用于实际的空域(北京管制区)中,与当前的扇区结构从扇区划分的安全性和负荷均衡性等方面进行了分析对比,仿真结果证明了算法的有效性。
[1] Yousefi A., Donohue G. Temporal and spatial distribution of airspace complexity for air traffic controller workload-based sectorization[C]. Chicago:AIAA 4th Aviation Technology, Integration and Operations (ATIO) Forum, USA, AIAA Paper 2004-6455.
[2] Drew M., Analysis of an optimal sector design method[C]. The 27thDigital Avionics Systems Conference, 2008, IEEE/AIAA, St. Paul., USA,3.B.4-1-3.B.4-1-10.
[3] Xue M. Airspace sector redesign based on diagrams[J]. J. Aerospace Computing, Information,and Communication, 2009, (6): 624-634.
[4] Trandac H., Baptiste P., and Duong V. Optimized sectorization of airspace with constraints[C]. The 5th USA/Europe Air Traffice Management Research and Development Seminar. 2003,
[5] Li J. h., Wang T., Savai M. and Hwang I.Graph-based algorithm for dynamic airspace configuration[J]. Guidance, Control, and Dynamics,2010, 33(4): 1082-1095.
[6] Basu A., Mitchell J., and Sabhnani G. Geometric algorithms for optimal airspace design and air traffic controller workload balancing[J]. ACM Journal of Experimental Algorithmics, 2009, 14(2.3): 1-28.
[7] Tang J. J., Alam S., Lokan C., and Abbass H. A. A multi-objective approach for dynamic airspace sectorization using agent based and geometric models[J]. Transportation Research Part C: Emerging Technologies, 2012, 21(1): 89 - 121.
[8] Idris H., Delahaye D. Distributed trajectory flexibility preservation for traffic complexity mitigation traffic mitigation[C]. California: 8th USA/Europe ATM R&D Seminar, Napa, USA, 2009.
[9] Stefan G., Mihaela U. Complex networks as control paradigm for complex systems[C]. 2007 IEEE International Conference on Systems, Man, and Cybernetics. Canada Montreal, QC, 2007, 4069-4074.
[10] 赵 鹏, 耿焕同, 蔡庆生, 王清毅. 一种基于加权复杂网络特征的K-means聚类算法[J]. 计算机技术与发展, 2007, 17(9): 35-40.
[11] Bi, H., Chen, Y.Z., Zhang D.F., Song Z. X.Optimization of airspace sectorization based on weighted graph and hybrid encoding genetic algorithm[C]. Beijing: The 12th COTA International Conference of Transportation Professionals. 2012,China: 1891-1902.
