基于ARMA时序分析模型的巷道围岩变形预测

卜庆为

(内蒙古科技大学矿业工程学院， 内蒙古 包头市 014010)

矿井建设中，根据巷道的服务范围把巷道分为开拓巷道、准备巷道和回采巷道，而每一种巷道具有不同的服务年限，所以各种巷道的支护技术和方法就会有不同考虑。近年来国内外的专家学者对软岩巷道进行了大量的研究工作，并取得了许多成果，但是不少矿井的支护方式在很多种情况下并没有充分考虑巷道服务年限的影响，由此往往增加巷道的维修工作量。

近些年来，广大采矿研究学者和工程技术人员期望可以从巷道变形的监测数据中找到其中蕴含的规律，以便预测将来的巷道变形。随着矿井向深部开采，巷道围岩流变的控制成为深部矿井巷道支护的研究热点[1]，应用时间序列分析法[2-3]预测巷道围岩变形量[4-9]，可以更好地判断巷道支护工程是否满足巷道在服务年限内正常生产的要求；对于高应力巷道采取一次让压二次抗压的支护方法，该支护方法也需要围岩变形的时间参考依据，以确定二次支护的最优时间段；围岩变形时间序列分析，利用有限的已观测数据对巷道服务期限内围岩变形进行预测，不仅反映巷道在服务期限内的围岩变形规律，还可以对服务期限内各个时刻的围岩变形量实现预报，最终起到“新奥法”支护技术的监测与及时反馈的作用。

1 巷道围岩变形观测

1.1 巷道围岩径向位移的数学模型

巷道围岩变形与围岩条件和围岩变形因素有关。从围岩体在应力重分布过程中变形特征的角度分析，Burgers本构模型可以接近实际描述围岩在各个蠕变阶段变形特征，是较为广泛使用的岩石流变本构模型。本文以Burgers本构模型建立巷道围岩径向位移的数学模型。

由弹性力学方法求解开挖巷道的围岩径向位移公式，本文直接引用弹性轴对称问题结果，弹性体巷道围岩的径向位移公式为：

根据岩体流变力学[1]得知，对于粘弹性体的井巷工程问题，借助拉氏变换，将弹性常数转变为粘弹性岩石的粘弹性常数，再通过拉氏变换的反变换进而求得粘弹性井巷工程问题中的粘弹性解。

1.2 基于ARMA的巷道围岩时序分析模型

运用高斯-牛顿法对拟合函数参数非线性回归分析，基本思想是对拟合函数进行泰勒级数展开，通过迭代修正拟合函数的参数，根据最小二乘法原理使拟合函数的参数逼近非线性回归模型的最佳参数值，即：

Y=f(t,a,b,c,d)

令g1，g2，g3，g4分别为拟合函数参数a，b，c，d的近似值，得：a=g1+δ1;b=g2+δ2;c=g3+δ3;d=g4+δ4。

对拟合函数Y进行泰勒级数展开，取其线性项，得：

Y=f(ti,g1,g2,g3,g4)+Σf′(ti,g1,g2,g3,g4)](j=1,2,3,4)

最小二乘原理，建立目标函数Q：

Q=Σ[y-Y(t)]2，

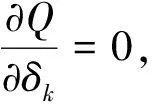
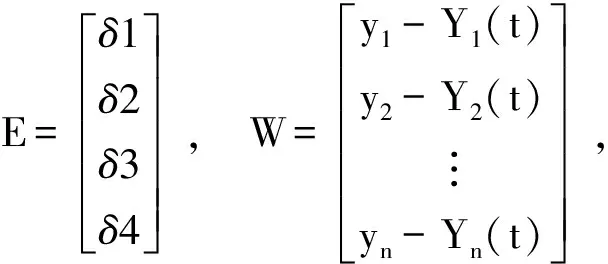
从而得E矩阵：

E=(F′TF′)-1·(F′TW)

由此, 解得拟合函数的参数误差δ1,δ2,δ3,δ4带入拟合函数的参数近似值g1，g2，g3，g4中，通过迭代计算以求得最佳拟合函数，进而得拟合函数Y(t)和误差集合W，然后集合W进行自回归分析(AR)。

围岩变形影响因素复杂多变，但考虑到t时刻的数值不仅与该时刻以前的自身值有关，同时还与其过去时刻的自身扰动项存在一定关系。因此，建立给定自回归移动平均模型(差分方程形式)：

式中：wi为拟合函数误差集合W中的元素，qi为自回归(AR)的系数，pi为移动平均(MA)的系数，ri为扰动项。

对于自回归(AR)模型，采用广泛使用的最小二乘法估计自回归系数，其精度相对矩估计的精度要高。对于移动平均(MA)部分中ri是不可观测的，因此该模型系数(qi，pi)采用非线性最小二乘原理，借助迭代法求得线性化近似解。公式如下：

设qi=qi0+αi，pi=pi0+βi，得S矩阵，于是有：

式中：w*和r*分别为wi和ri的一维列矩阵。根据非线性最小二乘，列目标函数，求解近似模型参数，公式为：

S=(QPT·QP)-1·(QPT·Rt)

将计算得到的α和β代入模型系数q、p中，循环迭代得围岩变形的时间序列模型参数。

1.3 ARMA模型围岩变形预测过程

设t时刻的下一时间间隔v时的预测值为w(v)，当v=1时,该模型差分方程：

当v=2时，则模型差分方程为：

对于rt+v，由于w(v)是对未来时刻的期望值，因此在预测过程中令预测值的扰动项rt+v=0，得一般式为：

至此，通过w(v)公式，通过由t时刻等以前观测数据构建的ARMA(m，n)模型预测任意等时间间隔的预测值，并与拟合函数Y构成实际预测值Zt。将拟合函数和ARMA(m，n)模型一同编制成为程序，这样就可以获得Zt=Y(t+h·v)+w(v)；其中h为间隔时间。

2 工程实例

测站布置在永华一矿12021工作面上、下巷，前期观测主要在12021工作面下巷。测站布置紧跟掘进工作面，距掘进工作面3 m远位置。通过测站监测数据，对顶板下沉量进行时间序列预测分析。

如表1 所示，已知数据观测时刻为2 d，确定模型参数所用数据时刻1～8，ARMA时序预测时刻9～12。如图 1 所示，通过对比分析，可以看出：实测数据围绕着预测数据发生上下波动。实际工程中，主要是由于巷道围岩自身复杂构造条件等因素，如节理、裂隙、围岩局部不均匀等因素，所以根据围岩的本构方程，结合时间序列分析方法进行分析，出现实测数据围绕着预测数据发生上下波动的现象，但误差变化规律具有明显的趋势性。分析后的该巷道时间序列分析预测公式为：

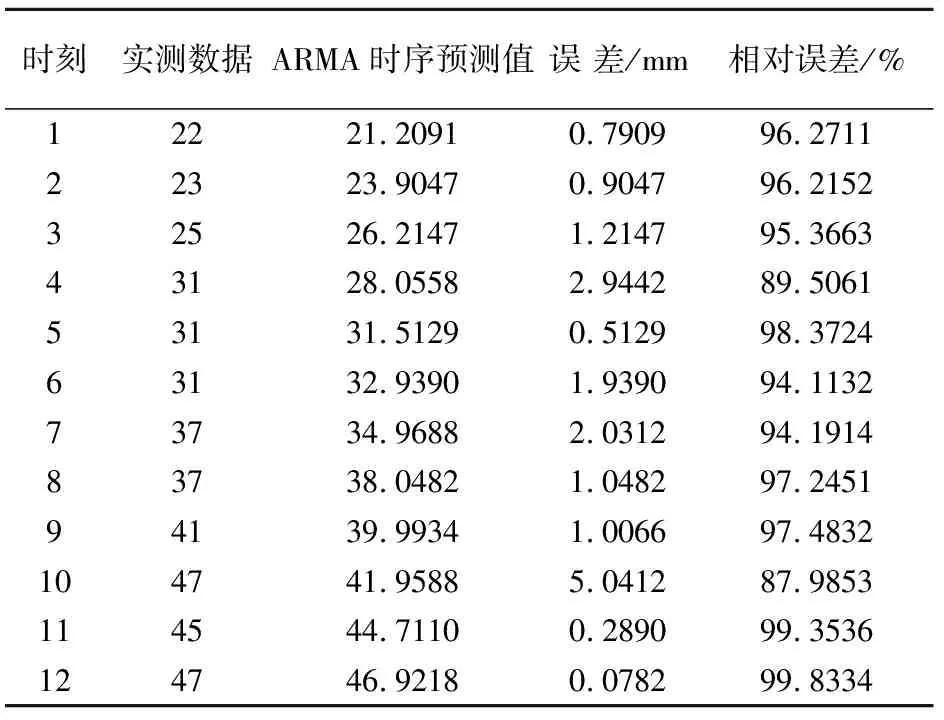
表1 工程实例数据比较

3 结 论

(1) ARMA时间序列预测的数学模型生成的曲线初期会呈现出一定的抖动、不平稳的特征，随时间的向前推移，预测曲线逐渐平稳。说明开挖巷道围岩自身会自发地通过围岩体变形来适应围岩所处的围岩应力环境，通过逐渐变形来实现自稳。

(2) 基于时间序列预测巷道围岩变形时序预测法相对单一的非线性函数数值拟合，不仅考虑到整体的围岩变形量与岩石参数和时间存在的非线性关系，而且强调了围岩变形受到来自围岩体内部自身复杂构造条件对围岩变化的干扰；当观测数据充足时，可以估算最终的围岩变形量以及自稳变化所经历的时间，否则会导致较大误差，不能正确反映应力重分布的过程，围岩变形的实际情况。

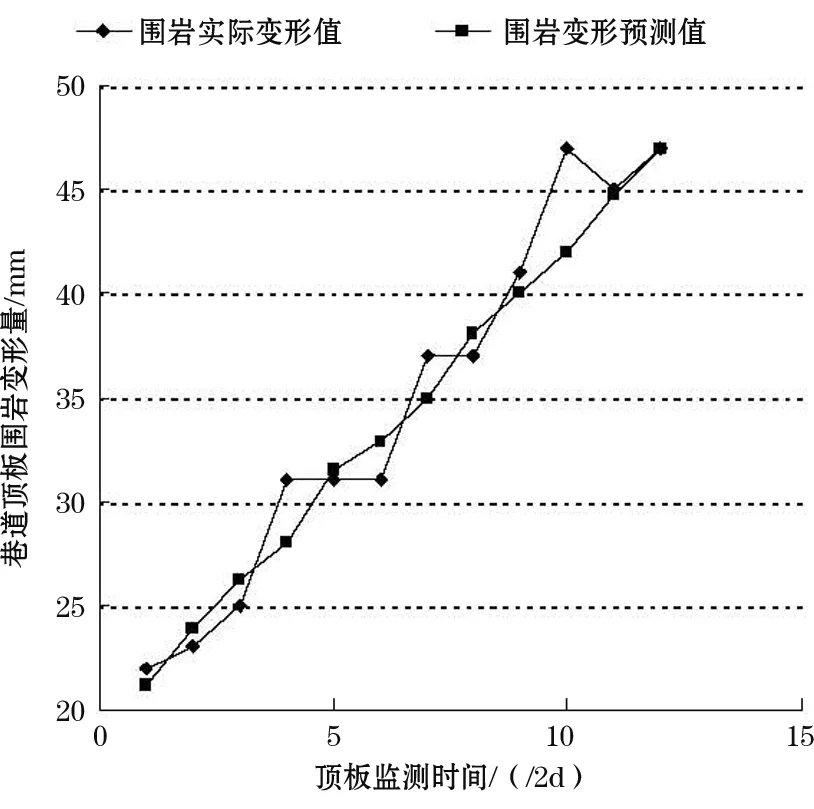
图1 工程实例实测数据与预测值数据比较

(3) 由于围岩变化所受到的干扰与其自身围岩条件、应力环境、开挖和支护工艺、巷道断面等诸多因素都有关系。不同的巷道围岩条件，围岩变形具有其自身的独特性，利用时间序列模型可以建立不同巷道围岩条件下该巷道所特有的围岩变形随时间变化的特征曲线；随着监测数据的更新，巷道变形特征曲线也会得到更新，进而更加贴近实际情况，不至于因为围岩岩性参数的差异而产生较大误差。

(4) 通过时序预测分析法和巷道变形监测数据建立围岩变形时序分析模型，以现场的支护-围岩相互作用的共同体作为研究对象，更加贴近工程实际对巷道服务年限内的巷道围岩变形量进行预测，及时反馈给支护设计者调整支护参数、优化支护设计方案。

参考文献：

[1]蔡美峰.岩石力学[M].北京：科学出版社,2002.

[2]王振龙,胡永宏.应用时间序列分析[M].北京：科学出版社,2007.

[3]李庆杨，王能超，易大义.数值分析[M].武汉：华中科技大学出版社,2006.

[4]史玉峰,孙保琪.时间序列分析及其在变形数据分析中的应用[J].金属矿山,2004(8)：13-15.

[5]王永岩，马士进，高 菲.软岩巷道围岩变形时序预测方法的研究[J].辽宁工程技术大学学报(自然科学版),2001,20(4):505-506.

[6]谭 赟.时间序列分析模型构建与MATLAB实现[J].科技通讯,2009(36):254-256.

[7]张玉祥.岩石工程时序列预报问题初探[J].岩石力学学报与

工程学报,1998,10(5):32-35.

[8]张长亮,王晓雯,陈 华.隧道围岩变形预测预报方法研究[J].公路交通技术,2008(4):88-92.

[9]廖野澜.监测位移的灰色预报[J].岩石力学与工程学报,1996,15(3):269-274.