基于瞬态热阻抗模型的氧化锌压敏电阻散热能力研究
2014-03-21行鸿彦杨天琦宋晨曦
张 欣,行鸿彦,杨天琦,宋晨曦
(1.南京信息工程大学,江苏省气象灾害预报预警与评估协同创新中心,江苏南京 210044;2.南京信息工程大学,中国气象局气溶胶与云降水重点开放实验室,江苏南京 210044;3.南京市气象局,南京市气象服务中心,江苏南京 210009)
0 引言
MOV型电涌保护器(Surge Protection Device,SPD)因其自身特有的泄放电流能力、非线性性质、残压限制水平等在现代防雷技术中受到大量研究人员的关注[1-7]。随着智能电网及信号传输系统对电压保护水平要求的提高,人们在SPD因故障模式影响其正常工作等问题方面做了大量的研究工作[8-13]。除了冲击老化劣化外,MOV芯片在各种非正常工作状态下因热量累积过快、散热能力不足致使其温度过高而引起的热熔穿和热劣化同样会影响其对电流的泄放[14],因此,对于MOV芯片散热能力与热量累积之间相互关系的研究也十分重要。
文献[15]提出MOV芯片因制造工艺的差异导致局部电位梯度过高、电流密度过大、局部温度升高,不均匀热应力导致其局部过热熔穿或炸裂。除此以外,MOV的热熔穿热劣化过程与芯片在交直流下对热量累积的吸收能力,以及芯片的散热能力等都有直接关系[16]。
目前,MOV芯片对热量吸收能力的研究多基于实验验证,结果表明,MOV对热量的耐受能力与MOV电压梯度、低温焊锡连接点位置、通流容量、能量耐受密度等有关[17],一般直流电比交流电造成的发热量大10%左右[18]。
对于MOV芯片散热能力的研究,同样基于对热量累积的试验分析上。通过对比不同参数芯片热量累积耐受能力的大小,间接得知MOV散热能力与其制造工艺及片径有直接关系[15-16]。杨天琦等[17]在分析MOV交直流电热量累积对比中,提到可以将直流电和交流电热量累积统一到“热阻”概念上,解释为:“引起单位温度变化所需的电功率”。这一概念与传统试验方法和实验条件无关,对于反映热量累积比“电流有效值”更具体直接。其他研究学者又提出了根据SPD热阻值,对其热稳定性进行判别的方法。研究结果表明,热阻的引入可直接表征其散热量的大小[10];并指出,热阻为热量转移时受到的阻力大小,其值与芯片厚度L和表面积S有关,但并未给出热阻的数学模型。
这些对SPD热累积的研究对实验条件依赖性较强,容易受到试验设备、环境及方法等干扰。基于热阻概念,结合MOV热熔穿试验结果,文中提出能够表征MOV瞬态散热能力大小的瞬态热阻抗模型,在此基础上,分析不同电流对MOV热阻的影响,实现定量表征MOV散热能力。
1 MOV瞬态热阻抗模型的建立
当热量在物体内部以热传导的方式传递时,将反映阻止热量传递的能力的综合参量定义为热阻[19],即在热平衡条件下,两确定的点(或区域)温度差与产生此温度差的耗散功率的比值,单位为℃/W.其表达式为:
(1)
式(1)假设耗散功率产生的全部热量流经热流路径。对于MOV芯片而言,发热是因为流经其内部的电流产生的热量累积效果,而热量消散快慢则与热量在流经热流路径时遇到的阻力大小有关。因此,热阻能够反映芯片与空气间传热能力的大小,即热阻大小可直接反映MOV芯片散热能力的大小。当MOV芯片在热量消散过程中,遇热流路径阻力大即热阻大时,其热量消散慢,散热能力差;反之,当热流路径阻力小时,热量消散快,其热阻小,散热能力好。
热阻是半导体器件的重要参数,文献[18]将热阻应用在SPD热稳定方面,用热阻代替电流有效值,定义热阻为产生单位温度变化所需消耗的电功率。即:
(2)
根据式(2),试验需测得在额定功率Pa下,SPD热稳定温度Ta,以及约2倍额定功率Pb下热稳定温度Tb,即可得到SPD的热阻值R。此模型反映了SPD热平衡状态下温升与电功率的关系,对于改进SPD热稳定热脱扣试验具有重要意义。
MOV芯片在交、直流下温升的变化是反映芯片热量累积和散热能力综合效果的参量,温升的变化正比于热量的净剩值的变化,即:Δt∝Q累积-Q散热。而温度变化与时间呈非线性关系[16],热量累积Q累积与通过MOV芯片的电流大小,通电时间呈线性关系,这就意味着,MOV芯片的散热量Q散热是随着通电时间变化的量。
为反映MOV芯片在非热平衡状态下的散热能力,引入瞬态热阻抗Z(t),定义为:在某一时间间隔末,结温Tj和基准点温度Tr之差的变化量,与引起该温差变化的同一时间间隔初始时阶跃变化耗散功率P之比,即:
(3)
瞬态热阻抗是一个非稳态的热阻,是芯片在通电加热及断电冷却的瞬间或芯片未达到热平衡状态前与时间、温度相关的瞬态热阻值。其最大值与稳态热阻值相等。且发生在芯片达到热平衡时。瞬态热阻抗是MOV芯片的一个特性量[19],其单位为℃/W.
在MOV芯片热熔穿实验中,对芯片通电时间为连续时间,设某时刻t1和t2间隔Δt时间,t1时刻芯片温度为T1,即:Tj(0)=T1,t2时刻芯片温度为T2,即;Tj(t)=T2,当Δt∝0时,即为瞬时,基准点温度变化可忽略,所以:Tr(0)=Tr(t),带入式(3)得:
(4)
(5)
由式(3)、式(4)、式(5)可知,瞬态热阻抗是热阻的一种,定义MOV的瞬态热阻抗为Rt,则有:
(6)
式(6)即为适用于MOV芯片的瞬态热阻抗模型。分析该模型知,MOV芯片的瞬态热阻抗与3个参数有关,是一个变化量。由于MOV芯片的瞬态热阻抗可表征芯片非平衡状态下散热能力,所以散热能力也是一个变化量。
2 MOV热熔穿试验
为研究散热能力与哪些因素有关,设计MOV恒定电流热熔穿试验,由于芯片发热量与通过的电流正相关,所以采用恒流试验;直流电流产生的热量累积比交流电流产生的大很多,熔穿时间较短,瞬态热阻抗变化过快,不易捕捉到热熔穿过程中的变化,并且SPD工作状态环境多为交流,因此,此次试验采用恒定交流电流试验。
2.1试验方法
试验采用同一厂家片径分别为25 mm和32 mm的2种MOV芯片各9片作为试验样品,按照片径大小分为A组和B组,再将每组试样均分为3小组,即:A1、A2、A3和B1、B2、B3组。试验前测量各试样的静态参数,其中,压敏电压U1mA、漏电流IL和非线性系数α采用CJ1001型压敏电压直流参数仪测得,标称放电电流In和最大放电电流Imax由厂家标示。静态参数如表1。
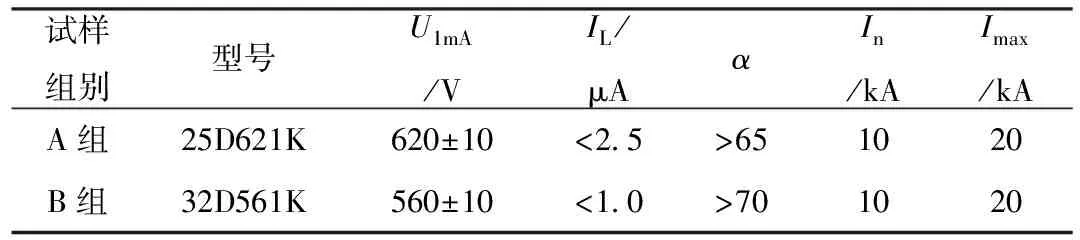
表1 试样静态参数
试验时环境温度为25 ℃,温度箱内初始温度为29 ℃,采用CJ1716型交流SPD热稳定试验箱试验。试验将6组试样通过不同的恒定交流电流,分别为A1、B1组通过40 mA交流电,A2、B2组通过50 mA交流电,A3、B3组通过60 mA交流电,与试验箱相连接的计算机利用软件方式实时显示通过试样的电流值、试样两端的电压幅值以及试样表面温度值。
试验直至试样温度达到最高点并开始下降时停止通电,此时试样两端的电压值已跌落60%以上,且表面有明显变形或烧坏痕迹,认为该试样已发生热熔穿现象。试验过程中,每隔相同的时间间隔记录一次电压和温度值,直至试样热熔穿为止。待试样冷却到室温后,测量试样静态参数,发现每一试样压敏电压均跌落10%以上,漏电流均大于20 μA,证明以上对试样已发生热熔穿的推断是合理的。
2.2试验数据分析
将测得的每一小组3片试样试验数据取平均值,分别得到A、B组的试样各通过恒定40 mA、50 mA和60 mA交流时,MOV试样温度及电压随时间变化的数据。其中,相同通电电流,A组试样热熔穿时间比B组长。并且,同一组中通过电流越大,热熔穿越快。如表2。

表2 试样通过恒定交流电流热熔穿时间
同样,分析试验数据得到MOV芯片温度上升的速率跟片径大小和通过电流值有关,如图1所示。图中3条曲线分别是同样小片径的MOV试样,在通以40 mA、50 mA和60 mA的恒定交流电流时温度变化曲线,可以看出:片径相同的试样,通以不同电流,温度上升速率与通电电流大小呈正比关系。其中通以40 mA电流的试样,在350~420 s时间范围内温度达到最大值并且试样处于热平衡状态,之后发生热熔穿,温度下降;而通以50 mA和60 mA电流的试样,温度曲线上升明显比40 mA快,但温度达到最大值后没有热平衡状态,而直接熔穿。对B组试样分析同样支持该结论。
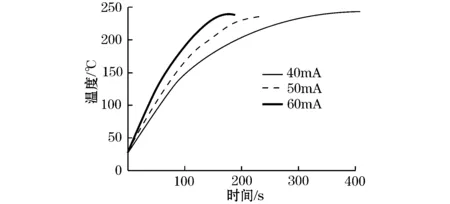
图1 A组MOV通过不同电流时温度随时间变化
由此可知,MOV芯片通以大电流时会导致芯片温度上升过快,研究表明,ZnO晶粒组成的双肖特基势垒与温度成反比关系[17],故温度迅速升高会使势垒高度下降过快,芯片急速热劣化,以至未能达到稳定势垒高度就已发生熔穿,晶界也随之消失[20-21]。
相同电流下,不同片径的试样,温度变化也不相同,如图2、3所示。图2中,试样通以相同的40 mA电流,A组试样温度上升速率大于B组。通电电流相同,即热量的累积量相同,而温度上升快反映热量累积量与散热量综合后的净剩量大,由此可以得出,小片径试样的散热量明显比大片径小,说明散热量与MOV芯片片径呈正比关系。图3是A2、B2组试样通过50 mA电流时温度的对比图,同样证明以上结论。
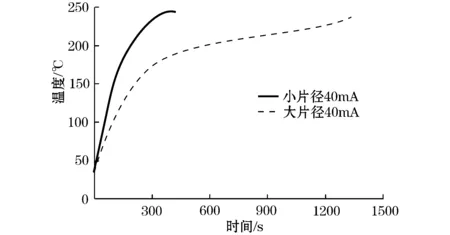
图2 A1、B1组MOV通过40 mA电流时温度随时间变化
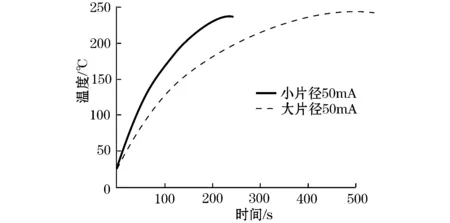
图3 A2、B2组MOV通过50 mA电流时温度随时间变化曲线
3 基于瞬态热阻抗模型的MOV散热能力分析
利用建立的适用于MOV芯片的瞬态热阻抗模型,可计算MOV芯片非平衡状态下瞬时热阻抗值,分析得到各参量对MOV芯片散热能力的影响。
3.1片径对散热能力的影响
此前研究者多认为,MOV芯片散热能力大小可直接根据片径大小判别[15-16],但均未能用具体的参数说明不同片径的芯片散热量随时间和温度的变化关系。定量研究片径不同MOV散热能力,可利用式(6)进行计算。
在瞬态热阻抗模型中,温差是影响热阻值大小的关键因素,故要求计算MOV瞬态热阻抗值时,应按照相同的时间间隔截取温度及功率值。图4和图5 中A、B组的MOV试样分别通过大小相等的恒定电流,以保证在随时间的变化过程中,热量的累积量是大小相等恒定不变的。相同温度下,芯片势垒高度相同,非线性相当,其瞬态热阻抗与温度的变化关系即能代表试样瞬时散热能力的变化过程。图中,A、B组MOV试样的瞬态热阻抗值并非一恒定值,而是随着温度的升高呈递减下降,相同的温度值下,A组试样热阻值大于B组试样,说明MOV芯片的散热能力随温度的升高而增大,并且相同温度下,小片径芯片的散热能力小于大片径。
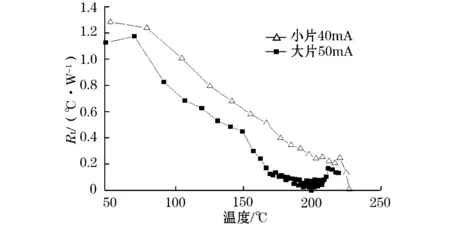
图4 A1、B1组MOV通过40 mA电流时瞬态热阻抗随温度变化曲线

图5 A2、B2组MOV通过50 mA电流时瞬态热阻抗随温度变化曲线
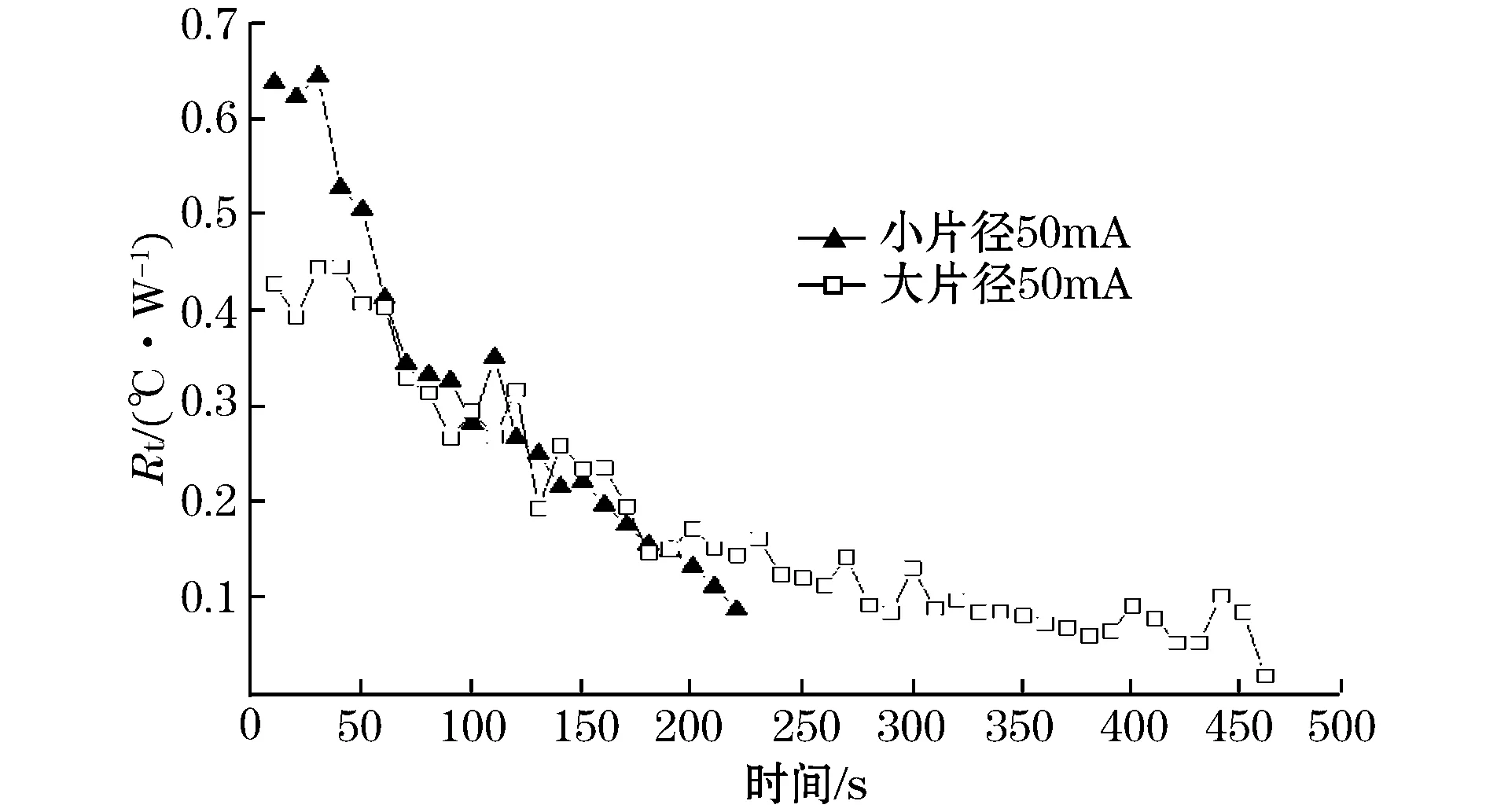
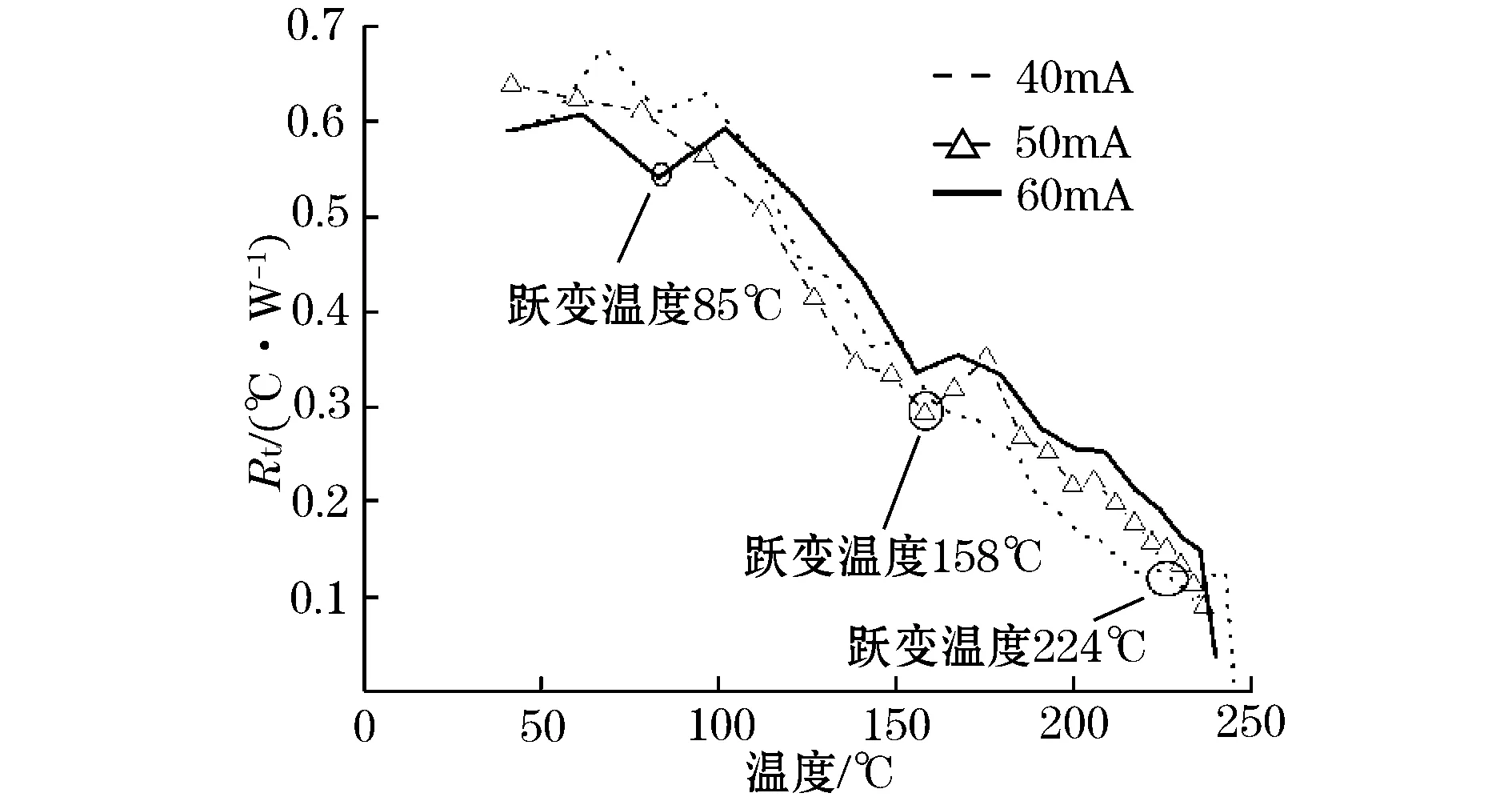
在热熔穿先期阶段,因散热量增大值不足以抵消热量累积的递增量,Q累积>Q散热,Δt>0,温度升高;当热阻值增大至散热量等于热量累积量时,Q累积=Q散热,Δt=0,温度不再上升,试样进入热平衡状态,如图2、图3中B组试样所示。通电电流对试样继续保持热劣化作用,持续高温将导致晶界层耗散,散热量加大,Q累积>Q散热,Δt>0,温度升高;当热阻值增大至散热量等于热量累积量时,Q累积=Q散热,Δt=0,温度不再上升,试样进入热平衡状态,如图2、图3中B组试样所示。Q累积 以上结论同样证明此前研究者得出的MOV芯片片径大小正相关其散热能力大小的结论,由此验证了所建立的适用于MOV的瞬态热阻抗模型的正确性。 MOV芯片通过大小相同的恒定电流时瞬态热阻抗是随时间变化的值,如图6、图7所示。A组试样热阻值下降速率大于B组,可知试样温度升高较B组快,其散热能力低于B组。由此可知,片径不同的MOV芯片,热阻值下降速率与热熔穿时间呈反比,间接证明MOV芯片片径与热熔穿时间成正比。 图6 A1、B1组MOV通过40 mA电流时瞬态热阻抗变化曲线 图7 A2、B2组MOV通过50 mA电流时瞬态热阻抗变化曲线 3.2热熔穿电流对散热能力的影响 针对通电电流值不同引起的MOV芯片热量累积,此前多数研究者做了大量试验分析[14,16-18],但均未提及在不同通电电流值下,热量消散对温升的影响。基于瞬态热阻抗模型,分析相同片径MOV试样通过不同电流值时瞬态热阻抗值随温度的变化关系,以A组试样为例,得到关系曲线如图8所示。 图8 A组MOV通过不同电流时瞬态热阻抗随温度变化曲线 图8中,瞬态热阻抗值随温度上升呈递减下降,温度在85 ℃左右之前,瞬态热阻抗值与通过电流值呈反比关系,85 ℃时,通以60 mA电流试样的瞬态热阻抗值发生大幅跃变,由0.54 ℃/W跃变至0.59 ℃/W,大于通电40 mA和50 mA试样的热阻值。而通以50 mA电流试样的瞬态热阻抗值在温度达到158 ℃左右也发生相同的跃变现象,热阻值由0.29 ℃/W跃变至0.31 ℃/W,之后相同温度下热阻值处于通电40 mA试样和通电60 mA试样之间。直至温度达到224 ℃,通以40 mA电流试样的瞬态热阻抗值发生跃变,大于通电50 mA和60 mA试样的热阻值。由此可见,相同片径的MOV芯片,通以不同电流,散热能力在达到某一“跃变温度”时会由原先的随温度上升而升高跃变为随温度上升而降低,致使温度较低时试样散热能力与通电电流值呈反比关系,跃变为温度升高后的正比关系。且不同的通电电流下,该“跃变温度”不同。B组试样亦如此。 由此可知,相同片径MOV芯片通过不同大小电流时,芯片的瞬态热阻抗值经历下降-增大-下降的过程,芯片散热能力并非单向变化,且通过电流越大,瞬态热阻抗跃变温度越低。 图9是A组试样通过不同电流值时热阻值随时间变化的曲线。图中,热阻值下降的速率呈正比关系,以此证明片径相同的MOV芯片,热熔穿时间与电流值呈反比。 图9 A组MOV通过不同电流时瞬态热阻抗变化 (1)在热阻概念的基础上,建立适用于表征MOV散热能力的瞬态热阻值模型。 (2)利用此模型,研究MOV芯片片径和热熔穿电流值对其散热能力的影响,定量计算了MOV散热能力。 (3)试验结果表明MOV芯片热阻值为一随时间变化的量,即热熔穿过程中,MOV芯片的散热能力是随时间延长其势垒高度降低同时散热能力增强。 (4)利用瞬态热阻抗模型计算得到,通过相同电流值,温度相同时,片径与瞬态热阻抗呈反比,即相同热熔穿电流作用下,同温度,MOV芯片片径越大,瞬时散热能力越好。 (5)片径相同的MOV芯片,热熔穿初期,瞬态热阻抗与通过电流值呈反比,随着温度升高,热熔穿过程中存在一个“跃变温度”,在此温度之后瞬态热阻抗值与通电电流跃变为呈正比,且“跃变温度”值与通电电流大小呈反比。 参考文献: [1]MANSOOR A,MARTAZLOFF F.The effect of neutral earthing practices on lightning current dispersion in a low-voltage installation.Power Delivery,IEEE Transactions on,1998,13(3):783-792. [2]AMICUCCI G L,FIAMINGO F,FLISOWSKI Z,et al.Surge protective devices for low voltage systems:practical approach for the protection distance evaluation.Power Tech,2007 IEEE Lausanne.Lausanne,2007. [3]DRABKIN M M.Surge protection of low-voltage AC power by MOV-based SPDs.Harmonics and Quality of Power,2002.10th International Conference on.Rio?de?Janeir,Brazil,2002. [4]HE J,CHEN S,ZENG R,et al.Electrical parameter statistic analysis and parallel coordination of ZnO varistors in low-voltage protection devices.Power Delivery,IEEE Transactions on,2005,20(1):131-137. [5]胡军,龙望成,何金良,等.ZnO压敏电阻残压比的影响因素分析.高电压技术,2011,37(3):555-561. [6]陈水明,魏旭.氧化锌压敏电阻电气参数分散性试验研究.高电压技术,1996,22(4):70-72. [7]章天金,周东祥,龚树萍.低压 ZnO压敏陶瓷冲击老化特性.电子元件与材料,1999,18(4):18-19. [8]杨仲江,张枨,柴健,等.氧化锌压敏电阻老化过程中非线性系数变化的研究.电子元件与材料,2011(9):27-30. [9]方义治.配网中MOA承受操作过电压的分析.高电压技术.2002,28(4):45-46. [10]王雪,莫娟,张冠军,等.MOA新在线检测系统及其仿真研究.高电压技术,2003,29(7):37-39. [11]陈青恒,何金良,谈克雄,等.氧化锌非线性电阻片微观结构及特性对电流分布的影响.中国电机工程学报,2002,22(8):62-66. [12]盛财旺,张小青.压敏电阻在雷电过电压作用下的可靠性.高电压技术,2013,39(2):437-442. [13]何金良,刘俊,胡军,等.电力系统避雷器用 ZnO压敏电阻研究进展.高电压技术,2011,37(3):634-643. [14]陈琳.MOV 型 SPD 测试及老化分析:[学位论文].南京:南京信息工程大学,2011. [15]郭洁.怎样提高 ZnO 电阻片的能量吸收能力.高压电器,2001(3):36-37. [16]杨仲江,李强,张枨,等.MOV 在交直流电压下耐受能力的试验研究.电瓷避雷器,2013(6):42-47. [17]应达,肖稳安,赵军,等.工频过电压对压敏电阻影响的实验研究.电瓷避雷器,2012(12):71-75. [18]杨天琦,王振会,朱传林,等.MOV型 SPD 在交直流电压下的热量累积对比分析.电瓷避雷器,2011(5):81-89. [19]秦贤满.热阻的概念和测试方法.半导体技术,1999(6):32-36 [20]宋晓兰.ZnO 压敏陶瓷中的次晶界、主晶界及其对电性能的作用:[学位论文].西安:西安交通大学,1993. [21]禹争光,杨邦朝.ZnO压敏电阻界面导电特性研究.功能材料,2005,35(6):709-710. [22]张郴莉.双脉冲电流作用下氧化锌电阻冲击老化破坏机理的研究:[学位论文].北京:中国科学院电工研究所,2001. [23]WOKTERS D R,SEHOOT J V.Kinetics of charge trapping in duekeetries.J Appl Phys,1985,58(2):831-837. [24]龚李伟,文远芳,孟毅.不同介质中MOV小电流区特性研究.高电压技术.2007,33(5):83-86. [25]陈新岗,李凡,桑建平,等.氧化锌压敏陶瓷伏安特性的微观解析.高电压技术,2007(4):33-37. [26]尹桂来,李建英,尧广,等.ZnO 压敏陶瓷冲击老化的电子陷阱过程研究.物理学报,2010,59(9):6345-635. [27]张美蓉.ZnO 压敏陶瓷老化机理的研究:[学位论文].西安:西安交通大学,1991. 行鸿彦(1962-),教授,博士生导师,主要从事智能化气象仪器设计与研究、计量技术与标准,微弱信号检测与处理,雷电防护技术与仪器等方面的研究。 E-mail:.edu.cn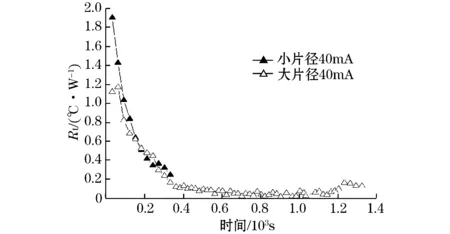
4 结论
