基于TSVD和Hilbert变换的相位差测量方法及应用

王国富，吕晓凡，高平东，张法全

(桂林电子科技大学信息与通信学院，广西桂林　541004)

0　引言

相位差的传统测量方法有基于模拟器件的脉冲计数法、矢量法等，电路本身的温漂等因素会使测量结果产生较大的偏差，抗干扰能力略显不足，且后续功能的可扩展性受限，测量准确度也很难提高。目前广泛采用的是将数据采集技术与信号处理相结合的方法，首先通过高速数据采集板卡或示波器同步采集2路信号，数字离散化后送至信号处理模块计算相位差。常用的信号处理方法有过零点法[1]、相关分析法[2-3]、频谱分析法[4-5]等。过零点法的本质是将时间差转换为相位差，为提高相位差的计算精度，在零点附近采用最小二乘法寻找最佳的拟合零点时刻。此方法原理简单，易实现，不足是检测交流信号时存在一定的失真，且在采样频率高，信号幅值较大时才能获得很好的测量效果。相关分析法通过2路信号的相互运算计算相位差，频谱分析法通过离散傅里叶变换将信号从时域变换到频域，通过分析相频特性计算相位差。两种方法都具有较强的抗干扰能力，且都利用三角函数的正交性，具有较高的准确度。相关分析法要求严格的整周期采样，而频谱分析法计算量大，存在频谱泄漏和栅栏效应，一般也要求整周期采样。文献[4]采用窗函数选择准则，克服了这些限制并取得了较好的效果。总体而言，每种方法各有优缺点。而希尔伯特变换在很早就应用于瞬时频率的测量，且结合经验模态分解(Empirical Mode Decomposition，EMD)实现了对多分量信号的分析处理，已取得较多研究成果，但在相位差测量方面研究较少[6-9]。文中在总结以往瞬时参数计算方法的研究基础上，提出了截断奇异值分解(TSVD)与Hilbert变换相结合的方法计算相位差，实现了对相位差的高精度测量，取得了较好的效果。

1　相位差测量方法

1．1TSVD降噪

对于mxn维的实矩阵，都可分解为3个矩阵Umxl、Λlxl和Vnxl，使得：

Amxn=UmxlΛlxlVnxlT

(1)

式中Λlxl是对角矩阵，对角元素λi(i=1，2，…l)为该矩阵的非负奇异值，且按降序排列。

保留前r个反映信号能量的主要奇异值，将剩余的奇异值置零得到新的对角矩阵Λlxl。用Λlxl替换原对角矩阵，通过式(1)得到重构矩阵Amxn，即可实现降噪。

假设其中一路受噪声影响的信号向量为X，其长度为N，使用TSVD对其降噪处理前，首先将其转换为m行n列的矩阵形式Amxn，形如

(2)

(3)

式中ΔEi表示奇异熵在截断数r处的增量。

其计算公式为：

(4)

信号的奇异熵反映了信息量饱和度，未受噪声干扰的信号在较低的重构阶次即可得到信息量的饱和，使奇异熵趋于一个稳定值；对于受噪声干扰的信号，随着重构阶次的增大，信号的奇异熵对应的信息量饱和度逐渐增大；当得到某一重构阶次后，信号奇异熵变换缓慢，若继续增大重构阶次，会引入噪声，此时奇异熵变化快慢的拐点对应理想的重构阶次，即为TSVD所需要的截断数。利用式(1)及重构方法得到重构矩阵Amax，从而得到降噪后信号向量X。

形如x(t)=0.01×(sin(4πft+π/4)+cos(2πft))的信号，频率为100 Hz，采集4个周期信号，分别加入SNR为9，6，3的高斯随机噪声，如图1所示。

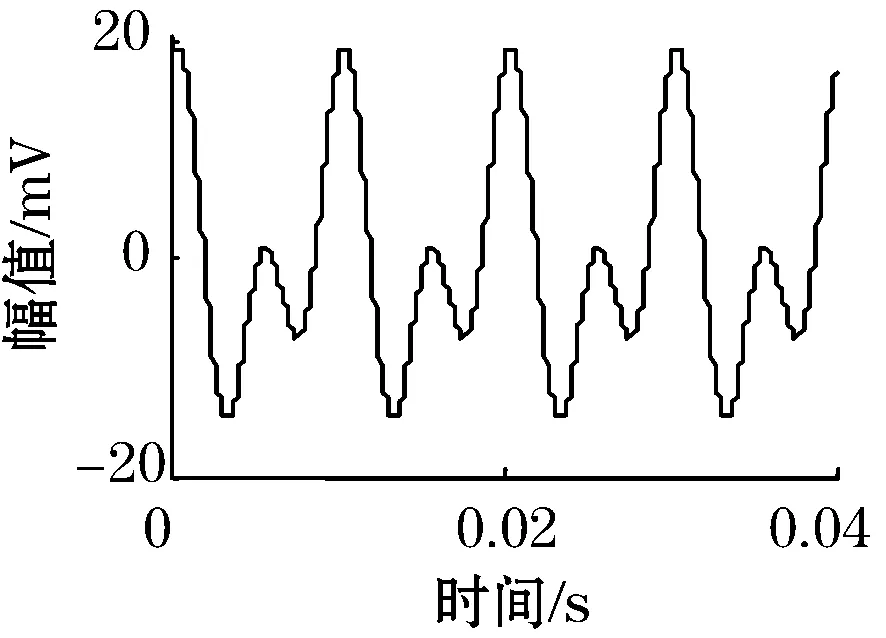
(a)

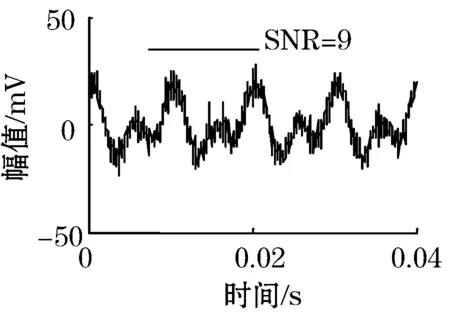
(b)

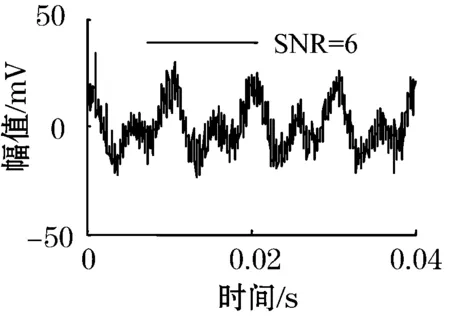
(c)

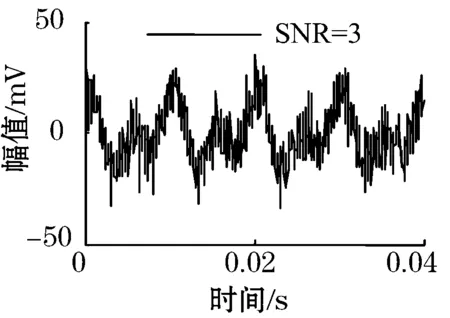
(d)

图2为奇异熵变化量随奇异谱阶次的变化曲线，从图2可发现，同一信号的最佳奇异谱阶次是一定的，该阶次不随信噪比的变化而变化。当有效信息量基本达到饱和状态后，奇异熵变化量变得很小，若再继续叠加更多信息量，可能会将噪声引入，反而不利于降噪。

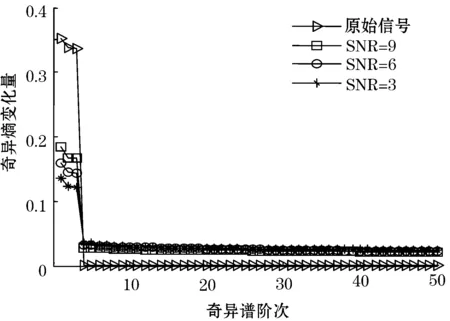
图2　奇异熵随奇异谱阶次增大的变化量

图3是根据TSVD降噪方法将信噪比为3的信号重构，得到与原始不含噪声信号的对比图，结论是通过奇异熵变化量的变化趋势确定最佳的奇异谱阶次，即TSVD截断数，应用TSVD降噪方法重构得到的信号与原始信号基本吻合。

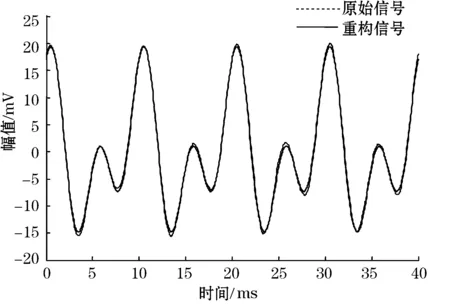
图3　原始信号与重构信号对比图

1．2Hilbert变换

希尔伯特变换可看作信号通过希尔伯特滤波器的输出，该滤波器的单位冲击响应为：

(5)

对希尔伯特变换作傅里叶变换，分析其幅频和相频特性可知，希尔伯特滤波器是幅频特性为1的全通滤波器，且具有相移90°的特点。信号X通过希尔伯特滤波器，负频率信号分量作+90°相移，正频率信号分量作-90°相移。

假定信号1和信号2分别为：

(6)

信号1与信号2的希尔伯特变换为：

(7)

作如下组合计算：

(8)

根据三角函数的和差化积性质得到式(9)：

(9)

显然，2路信号的相位差可由反正切得到式(10)：

Δθ(t)=arctan(za/zb)

(10)

从以上推导过程可知，整个过程不需计算频率值，幅值乘积分别处于分子分母中相互抵消，原始信号与Hilbert变换后的信号进行运算，仅发生相移，这为相位差计算提供了便利。

2　仿真分析

为了考察TSVD结合Hilbert变换的联合方法计算相位差的有效性，现分别分析信噪比、采样率两种不同条件下的计算效果。数值模拟的是核磁共振发射机与接收机信号相位差计算。

2．1信噪比分析

假设发射机激发信号的频率为1 987 Hz，发射包含10个周期的长度，接收机接收的信号幅值随时间变化指数衰减，采样频率为30 kHz，相位差为π/4，加入信噪比为2～70的高斯随机噪声。图4、图5分别是联合方法计算的相位差及相位差的绝对误差。

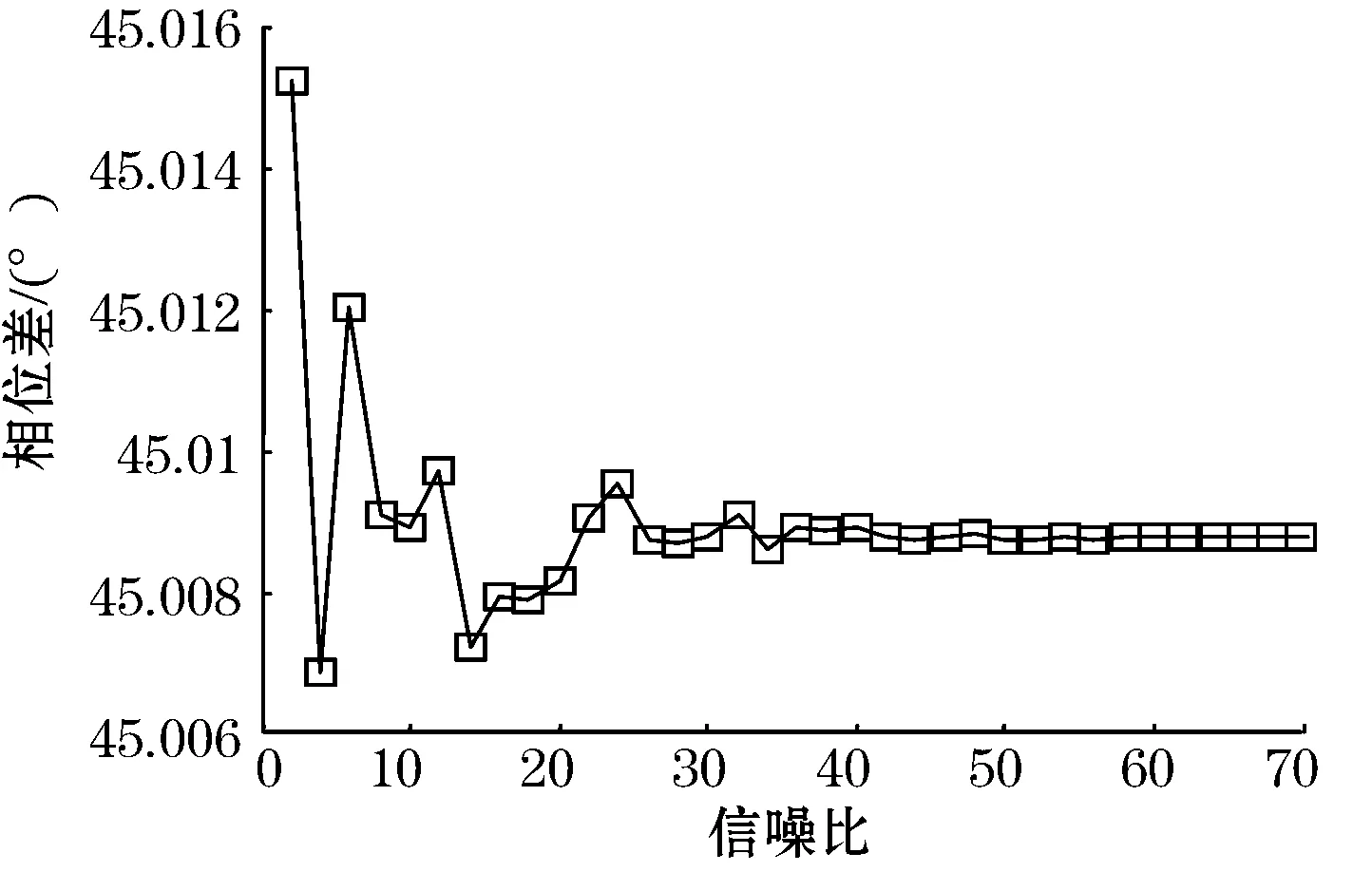
图4　不同信噪比条件下的相位差

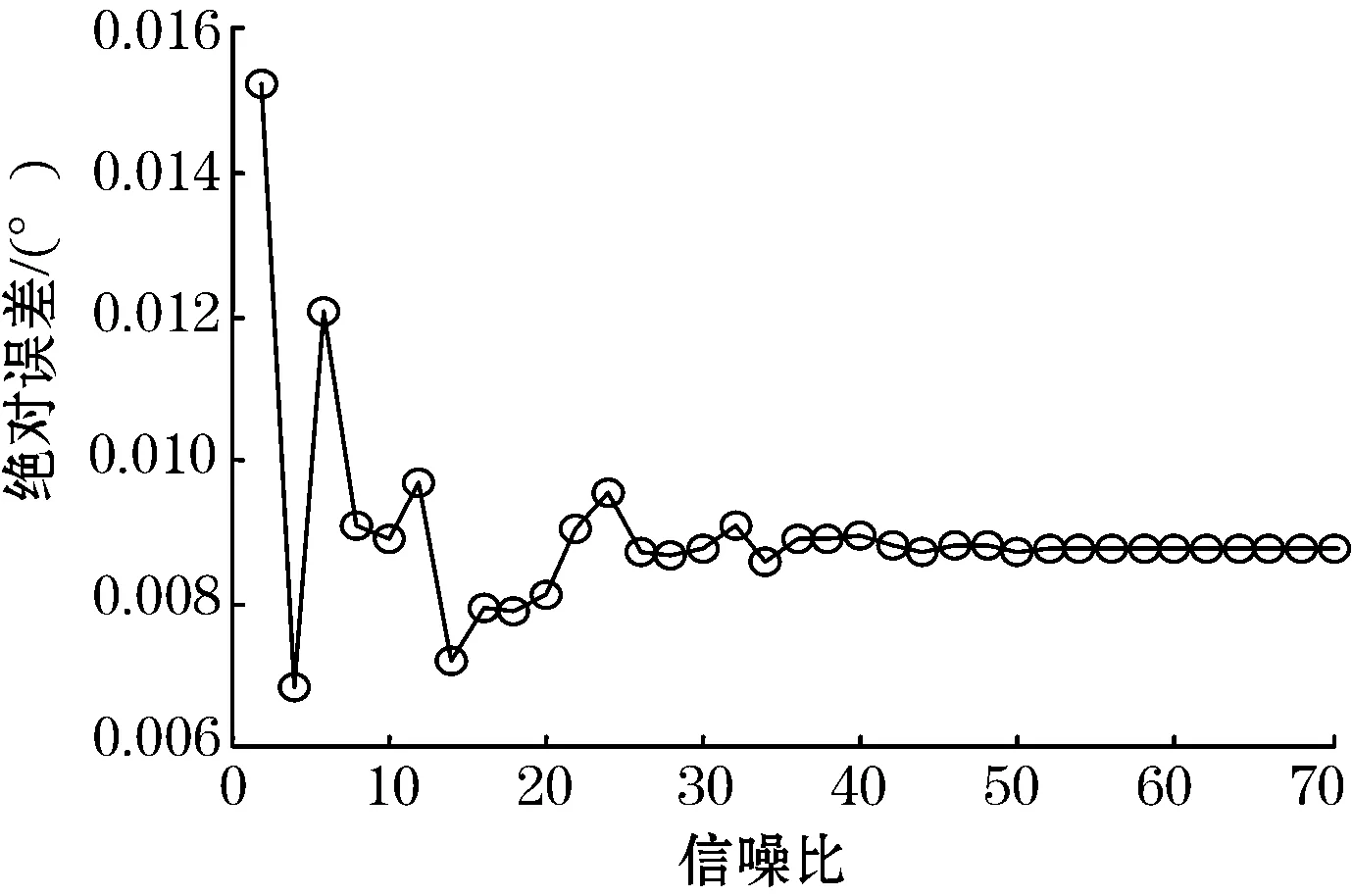
图5　不同信噪比条件下的相位差绝对误差

信噪比较低时也能够得到较好的相位差值，随着信噪比提高，相位差会动态调整并最终稳定在理论值附近。绝对误差显示了相位差计算过程中的偏差，联合计算方法优势明显。

2．2采样率分析

高于激发周期信号频率数倍的采样速率显然有利于相位差分析。为此，这里仅取原始激发信号频率的1～30倍采样速率进行分析。图6、图7 分别是联合方法计算的相位差及相位差的绝对误差。图6中，由于前两个采样率值分别是原始信号频率的1倍和2倍，不满足奎斯特采样定理，因此计算得到的两个相位差值错误。分析图6和7可知，经过10倍以上的采样率采集信号，采用TSVD结合Hilbert变换计算所得的相位差基本稳定，也就是说当采样率高于原始信号最高频率数倍时，相位差计算结果基本不受采样率的影响。

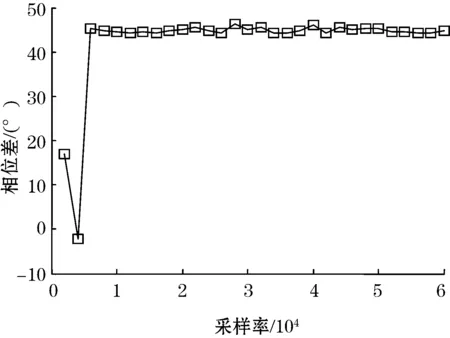
图6　不同采样率条件下的相位差

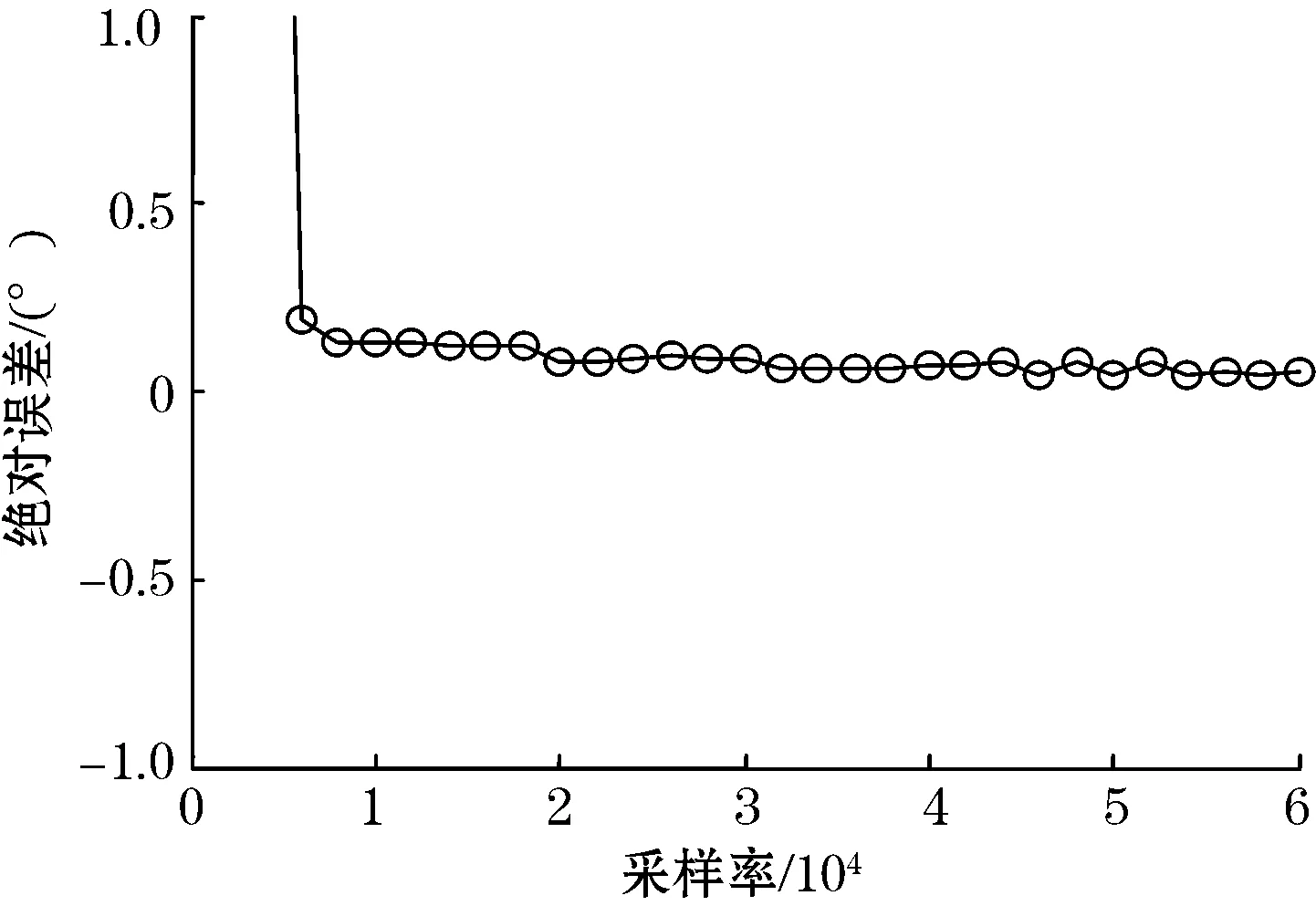
图7　不同采样率条件下的相位差绝对误差

3　实测数据验证

实际需求是测试发射信号与采集的弛豫衰减信号相位差。原始发射信号是正弦信号，接收的弛豫衰减信号是频率几乎不变，幅值呈指数衰减变化且含有干扰噪声的正弦信号。数据是4月下旬在广西百色那坡镇测得的野外实测数据。野外探测时采用了12个脉冲矩探测浅层含水量信息，计算每个脉冲矩对应的相位差，得到的12个相位差值可为后续的地球物理反演工作提供参考。采用LabVIEW软件开发平台设计相位差分析算法。根据1．2节的分析，相位差的联合计算方法不受幅值变化的影响，为了方便比较，在计算相位差之前，可先将衰减信号的幅值放大到原始激发信号的同一数量级。另外，由于采集时间长于发射时间，为便于计算，仅取与发射信号时间长度一致的信号段。以计算第3个脉冲矩采集的弛豫衰减信号为例计算相位差，计算结果如图8所示。受其他未知噪声干扰的影响，用实测数据计算的相位差没有仿真分析精确度高，但仍然稳定地测得了相位差，反映了脉冲矩对应的含水层导电性地质参数，这为后续反演工作提供了重要参考，满足实际应用需求。

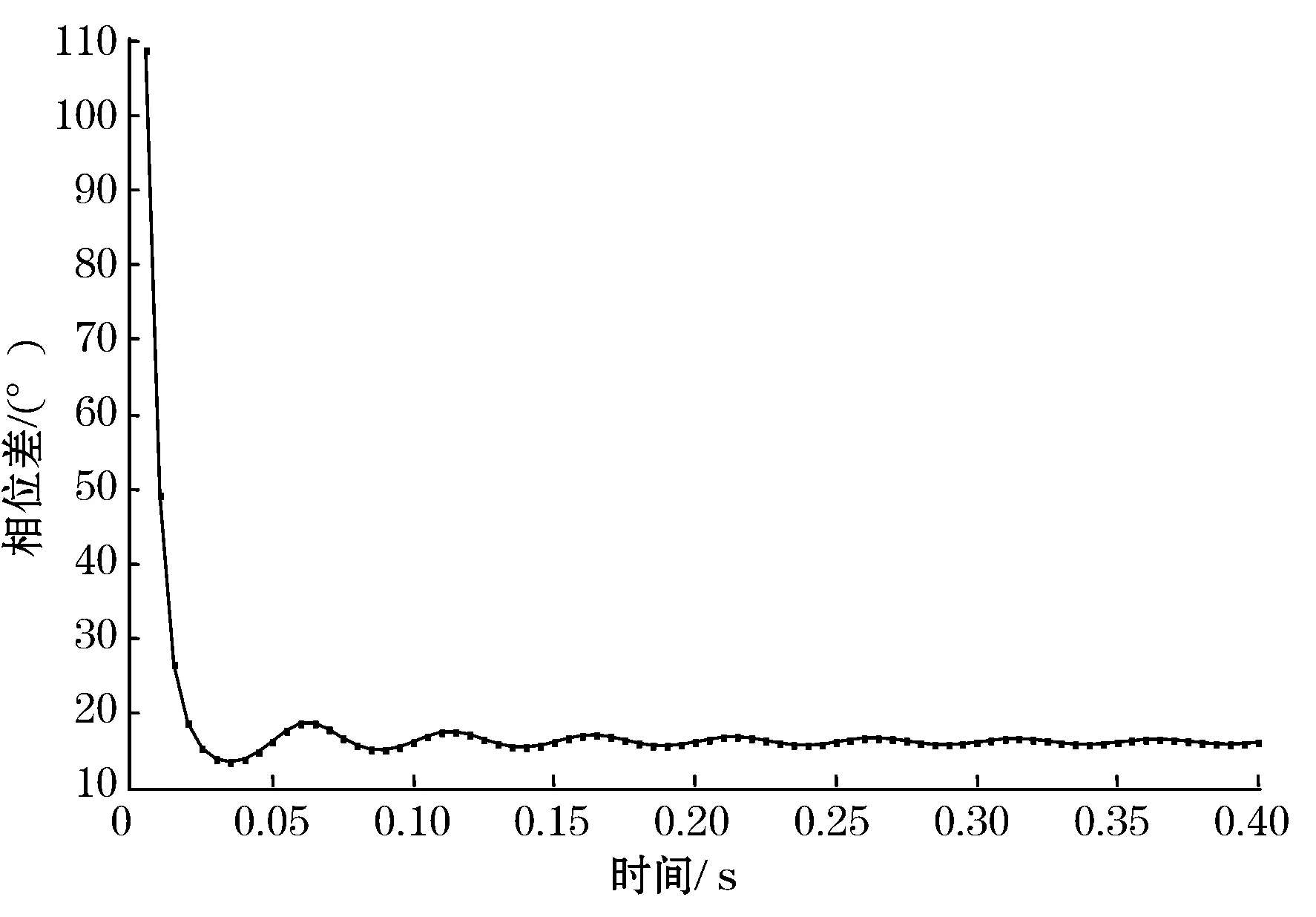
图8　弛豫信号与原始信号的相位差

4　结束语

TSVD降噪和Hilbert变换相结合的方法，很好地实现了相位差测量的工程应用，关键的一步是确定最佳的奇异谱阶次，尽可能地包含有效信息量且避免引入不必要的随机噪声信息。此联合方法属于一种较通用的计算方法，不需预知瞬时频率，不需迭代计算。因此速度较快，能检测微小相位差。需要说明的是，当信噪比极低时，任何一种方法均不能非常精确地计算相位差。对于更加复杂的信号，若不满足Hilbert变换的条件，可先通过EMD分解得到一系列的(IMF)固有模态函数，从中挑选有用的分量并重构，再用TSVD和Hilbert变换的联合方法求解相关联的两路信号相位差。

参考文献：

[1]吴俊清．基于虚拟仪器的相位差测量研究．北京理工大学学报，2005，25(5)：435-438．

[2]张毅刚，付平，王丽．采用数字相关法测量相位差．计量学报，2000，21(3)：216-221．

[3]桂任舟．基于虚拟仪器技术和互相关原理的相位测量仪．仪表技术与传感器，2004(5)：8-10．

[4]汪亚群，何怡刚．周期信号相位差的高精度数字测量．电工技术学报，2006，21(11)：117-126．

[5]吴俊清．相位差的数字化测量研究．应用基础与工程科学学报，2005，13(1)：99-104．

[6]陈平，李庆民，赵彤．瞬时频率估计算法研究进展综述．电测与仪表，2006，43(7)：1-7．

[8]SUNG N H，TA H C．A novel amplitude-only method of phase difference measurement between two signals by using 90° Hybrid．Proceedings of the Asia-Pacific Microwave Conference．2011：1806-1809．

[9]TU Y Q，ZHANG H T．Method for CMF signal processing based on the recursive DTFT algorithm with negative fre- quency contribution．IEEE Transactions on Instrument- ation and Measurement，2008，57(11)：2647-2653．

[10]杨文献，任兴民，姜节胜．基于奇异熵的信号降噪技术研究．西北工业大学学报，2001，19(3)：368-371．