熔融沉积快速成型零件成型方向的多目标优化

袁贝贝， 姜兆亮

（山东大学机械工程学院高效洁净机械制造教育部重点实验室，山东 济南 250061）

熔融沉积快速成型零件成型方向的多目标优化

袁贝贝， 姜兆亮

（山东大学机械工程学院高效洁净机械制造教育部重点实验室，山东 济南 250061）

为了实现熔融沉积快速成型（FDM）中零件成型精度和成型效率的协同优化，基于零件成型方向对成型精度和成型效率的影响进行分析，以体积误差最小、零件成型方向上高度最低以及所需支撑体积最小为目标，建立了零件成型方向的多目标优化模型。设计了基于非支配排序遗传算法的智能求解算法，通过对模型的优化计算得到零件成型方向的 Pareto解集，实现了 FDM 零件成型方向的智能优化。最后通过实例验证了所建模型的正确性与算法的有效性。

快速成型；成型方向；遗传算法；多目标优化

熔融沉积快速成型(fused deposition modeling, FDM)制造的零件具有成本低、强度高等优点，但其精度和成型效率之间的矛盾显著。影响FDM精度和效率的主要因素有零件的成型方向和分层厚度，其中，成型方向的选择会直接影响零件的表面质量、成型高度、支撑结构、成型效率以及强度等方面。因此，合理选择零件的成型方向可以实现成型精度与成型效率的协同优化。

目前，FDM中零件的成型方向主要依靠人工确定，对结构复杂的零件难以选出最优的成型方向。所以，国内外学者对快速成型方向的优化做了很多研究，Rattanawong等[1]将台阶效应量化成体积误差，以体积误差最小为目标优化零件的成型方向；刘厚才和储爱民[2]用遗传算法优化三维打印(3DP)的成型方向，以提高零件的表面质量；文献[3-5]建立了以支撑面积最小、制作时间最短以及零件表面质量最优为目标的数学模型，用遗传算法求解零件的成型方向；Thrimurthulu等[6]以平均表面粗糙度和成型时间为目标，用遗传算法优化FDM工艺的成型方向，得到针对不同的加权系数所对应的最优解；洪军等[7]以光固化快速成型中的悬臂变形、台阶效应、过固化及制作时间为目标，分别构造了子目标函数，利用评价函数法，把制作方向优化的多个目标函数转化为一个数值目标的评价函数来进行优化。上述研究主要以单一的优化目标或者以线性加权法将多个目标转化为一个目标进行研究，难以找到多个目标综合最优的成型方向，而且线性加权法中加权系数的确定需要人为做出选择，客观性较差。文献[8-9]以体积误差和零件高度为目标，用遗传算法得到两个目标的 Pareto解集；刘厚才和廖艳春[10]采用基于 Pareto最优解的多目标优化遗传算法对零件的成型方向进行优化，将优化结果与单目标优化方法进行比较。但是，上述研究很少考虑支撑体积对成型时间的影响，而且用支撑面积评价零件表面质量的方法对水溶性支撑材料不再适用。因此，本文对FDM零件成型方向的优化模型进行了补充和修改，并采用基于 Pareto解集的方法优化零件的成型方向。

1 分层方向多目标优化模型的建立

1.1 表面质量的优化模型

FDM制造过程中，随着成型截面的不断变化，会在零件的倾斜表面上产生台阶效应。比如，当图1(a)中的模型沿Z方向成型时，模型的光滑倾斜表面上会出现台阶效应，使表面变得粗糙，如图1(c)所示。台阶效应是快速成型的原理性误差，但是合理选择零件的成型方向可以使其显著降低。例如，当图 1(a)中的模型沿 Y向成型时，则不会产生台阶效应，这时零件的表面质量最好，如图1(b)所示。

图1 台阶效应

当台阶效应无法完全避免时，可以减小实际成型的零件和设计模型之间的体积误差以提高零件的表面质量。计算零件每一成型层上的体积误差，将各层体积误差相加得到整个零件的体积误差，并将其转化为 STL(stereo lithography)模型上各个三角面片引起的体积误差之和[5]，体积误差 f1如式(1)所示：

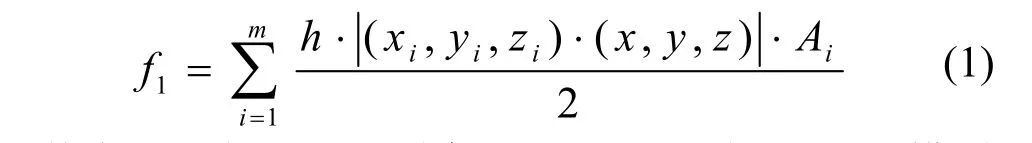
其中，h表示分层厚度， (xi, yi,zi)表示STL模型中第 i个三角面片的法向量， (x , y,z)表示零件的成型方向的单位向量， Ai是第 i个三角面片的面积， (xi, yi,zi)和 (x , y,z)均为单位向量。

快速成型中，分层方向的选择应该在分层厚度确定之前进行，FDM分层厚度一般取值范围为0.15～0.30 mm[11]，式(1)中的分层厚度 h取为0.20 mm。而且，当三角面片的法向量和成型方向的方向向量平行时，在该三角面片上不会产生台阶，因此，采用阈值函数 ε1将满足上述条件的三角面片从式(1)中排除，则台阶效应引起的体积误差 f1如式(2)所示：

1.2成型时间的优化模型

FDM中，零件的成型时间包括零件本身的成型时间Tm、辅助成型时间Ta以及支撑的成型时间Ts。零件成型时间[3]T，如式(3)所示：

其中，Vm为零件的体积，Vs为支撑材料的体积，vm为成型零件时的平均速度，vs为成型支撑时的平均速度，Ta(i)为第i层的辅助成型时间。

(1) 成型方向上零件高度的优化模型：零件每一层的成型时间包括喷嘴匀速运动的时间以及喷嘴加减速时间，零件分层数目越多，成型时喷嘴加减速的时间相对较长，零件成型的平均速度也就越低。另外，零件在进入下一层成型时，喷头需要沿z轴方向运动一个层厚的距离，分层数目越多，层与层之间运动的辅助时间就越长。可见，零件的成型时间和辅助时间都与零件的分层数目密切相关，而目前大多数的FDM成型工艺都是固定层厚的，因此零件的成型时间和辅助时间与零件在成型方向的高度有关，高度越小，成型辅助时间越短。零件在成型方向上的高度f2可以用式(4)表示：

其中，(xij, yij, zij）表示第i个三角面片的第j个顶点的坐标组成的向量。

(2) 支撑体积的优化模型：FDM 中，零件在成型时需要添加支撑，零件沿不同的方向成型所需的支撑体积不同，由式(3)可见，支撑体积越大，成型时间相应越长。支撑体积用需要添加支撑的三角面片在工作台上的投影面积和支撑高度的乘积表示，支撑高度用三角面片 3个顶点相对于工作台高度的平均值来近似表示，因此支撑体积的表达式f3如式(5)所示：

其中，ε2是判断三角面片是否需要添加支撑的阈值函数。

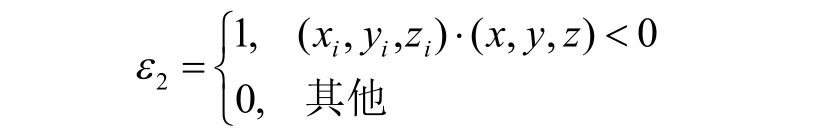
Zi1、Zi2和Zi3分别表示STL模型中第i个三角面片的3个顶点在成型方向上相对于工作台的高度。

2 分层方向多目标优化模型的求解

2.1成型方向的表示

上述优化模型中的向量(x, y, z)表示零件的成型方向，为单位向量，因此用单位球上的一点来表示零件的成型方向，如图2所示，其中x, y, z的数值都是在生成初始种群时随机产生的，因此向量(x, y, z)可能是空间中的任意向量。

图2 单位球

2.2 算法流程及参数选用

(1) 非支配排序遗传算法流程：遗传算法是一种模拟自然界生物进化过程和机制的智能优化算法，是求解多目标优化问题的有效方法。非支配排序遗传算法[12-13]是一种将 Pareto最优原理与遗传算法相结合形成的新型多目标遗传算法，可以在一个进化代中得到多个不同的 Pareto优化解，本文采用该算法对FDM成型方向的多目标优化问题进行求解，可实现FDM零件成型方向的智能优化，流程如图3所示。

图3 非支配排序遗传算法流程图

(2) 染色体编码方式：变量的编码方式选用二进制编码，方向向量的每个坐标值用十位二进制数表示，因此整个染色体用一个30位的二进制数表示，如图4所示。

图4 染色体的编码

(3) 遗传算子的选择：遗传算子对遗传算法的收敛性、收敛速度等都有影响，本文参照文献[14]并结合问题本身的特点设定表1所示的遗传算子。

表1 遗传算子

3 实例验证

为了证明上述模型的正确性和算法的有效性，从文献[15-16]中选择了如图 5所示的两个模型对该优化方法进行验证。

文献[15]模型由600个三角面片组成，用上述优化算法对其成型方向进行优化求解，求解结果如表2所示。

该模型的 Pareto解集中只包含一个解，它对应的成型方向为x轴方向，在该方向下3个目标均取得最优值，因此该模型最优的成型方向即为 x轴方向。3个目标的进化曲线如图6所示，从进化曲线中可以看到，在43代左右各目标收敛。根据所求成型方向的坐标值算出旋转角度α和β，本实例求得α约为0°，β约为90°，和文献[15]中的结果吻合。

文献[16]模型由 60个三角面片组成，同样的方法对其成型方向进行优化，结果如表3所示。

图5 成型方向优化模型

表2 文献[15]模型的优化结果

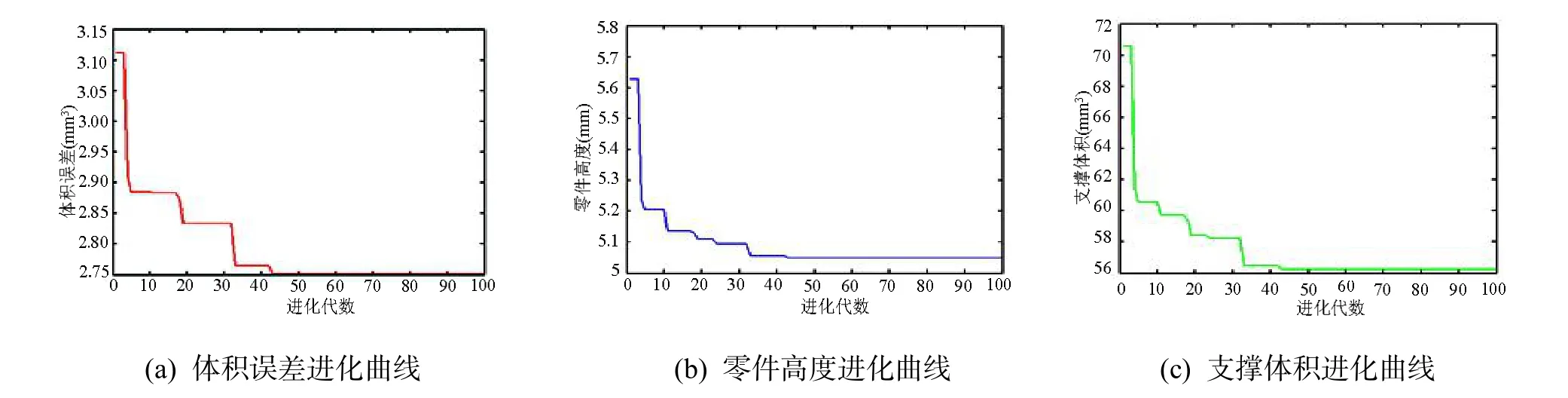
图6 进化曲线

表3 文献[16]模型的优化结果

从表 3可以看出，该模型的 Pareto解集由 3个解组成，其中，方向 1是零件成型高度最小的成型方向，方向 2是体积误差最小的成型方向，方向3是支撑体积最小的成型方向。与方向2相比，方向 1的零件高度和支撑体积明显较优，而且两个方向的体积误差相差不大，因此，总体上方向1优于方向2。方向1与方向3相比，方向1的体积误差较小，成型精度高，方向 1的零件高度小于方向3，但是方向1的支撑体积大于方向3，因此，两个方向成型时间的多少关系不能确定，可直接选择成型精度较高的方向1。上述3个方向分别对应文献[16]中的目标3、目标1和目标2，求解结果与文献[16]基本吻合。

以上两个模型的求解结果和文献中的结果相吻合，证明了模型的正确性和算法的有效性。而且该方法不必提前确定模型可能的最优成型方向，只需在整个单位球空间上进行一次优化计算即可找到全部的较优成型方向，用户可根据各自的偏好从中选择合适的成型方向。

4 结 论

结合水溶性支撑材料和FDM工艺的特点分别以体积误差最小、成型方向上零件的高度最低以及支撑体积最小为目标建立了FDM零件成型方向的优化数学模型，采用非支配排序遗传算法对其进行优化求解，得到Pareto解集，为用户提供多种可供选择的成型方向，用户可以从中选择合适的成型方向以满足成型精度和成型效率的最优组合。

[1] Rattanawong W, Masood S H, Iovenitti P. A volumetric approach to part-build orientations in rapid prototyping [J]. Journal of Materials Processing Technology, 2001, 119(1-3): 348-353.

[2] 刘厚才, 储爱民. 三维打印快速成型零件制作方向的优化研究[J]. 工程图学学报, 2009, 30(3): 41-45.

[3] 张卓辉, 李爱军, 杨金勇, 郝国丹, 王 欢. 基于遗传算法的快速成型零件分层方向优化方法[J]. 东华大学学报, 2010, 36(4): 376-380.

[4] 董 涛, 章维一, 王春晖, 王 伟. 快速成型制造中的零件分层方向优化新技术[J]. 计算机工程与应用, 2003, 39(1): 45-48.

[5] 赵吉宾, 何利英, 刘伟军, 卞宏友. 快速成型制造中零件制作方向的优化方法[J]. 计算机辅助设计与图形学学报, 2006, 18(3): 456-463.

[6] Thrimurthulu K, Pandey P M, Venkata Reddy N. Optimum part deposition orientation in fused deposition modeling [J]. International Journal of Machine Tool &Manufacture, 2004, 44(6): 585-594.

[7] 洪 军, 武殿梁, 李涤尘, 卢秉恒. 光固化快速成型中零件制作方向的多目标优化问题研究[J]. 西安交通大学学报, 2001, 35(5): 506-509.

[8] Zhang Jian, Li Ye. A unit sphere discretization and search approach to optimize building direction with minimized volumetric error for rapid prototyping [J]. The International Journal of Advanced Manufacturing Technology, 2013, 67(1-4): 733-743.

[9] Li Ye, Zhang Jian. Multi-criteria GA-based Pareto optimization of building direction for rapid prototyping [J]. The International Journal of Advanced Manufacturing Technology, 2013, 69(5-8): 1819-1831.

[10] 刘厚才, 廖艳春. 基于Pareto最优解的零件制作方向优化研究[J]. 工程图学学报, 2011, 32(1): 157-162.

[11] 张 媛. 熔融沉积快速成型精度及工艺研究[D]. 大连: 大连理工大学, 2009.

[12] 冯士刚, 艾 芊. 带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J]. 电工技术学报, 2007, 22(12): 146-151.

[13] 吴中元, 关志华, 李光泉. 一种改进的非支配排序遗传算法[J]. 北京科技大学学报, 2002, 24(6): 679-682.

[14] 关志华. 非支配排序遗传算法(NSGA)算子分析[J].管理工程学报, 2004, 18(1): 56-60.

[15] Cheng W, Fuh J Y H, Nee A Y C, Wong Y S, Loh H T, Miyazawa T. Multi-objective optimization of part building orientation in stereo lithography [J]. Rapid Prototyping Journal, 1995, 1(4):12-23.

[16] Lan Poting, Chou Shuoyan, Chen Linlin, Gemmill D. Determining fabrication orientations for rapid prototyping with stereo lithography apparatus [J]. Computer Aided Design, 1997, 29(1): 53-62.

Multi-objective Optimization of the Part Building Orientation in Fused Deposition Molding

Yuan Beibei, Jiang Zhaoliang
(Key Laboratory of High Efficiency and Clean Mechanical Manufacture of Ministry of Education, School of Mechanical Engineering, Shandong University, Jinan Shandong 250061, China)

In order to optimize accuracy and efficiency in fused deposition modeling (FDM), effect of the building orientation on part′s accuracy and efficiency is analyzed; meanwhile, three optimization models of part′s building orientation, i.e. volume error, height of parts in its building orientation, and support volume are established. A non dominated sorting genetic algorithm is designed to seek the Pareto optimal solutions of any complex model intelligently. Finally, the correctness of the proposed model and the efficiency of the algorithm are carried out based on two instances case study.

rapid prototyping; building orientation; genetic algorithm; multi-objective optimization

TP 391

A

2095-302X(2014)06-0835-05

2014-06-12；定稿日期：2014-07-02

国家自然基金资助项目(51175304)

袁贝贝(1988-)，男，山东潍坊人，硕士研究生。主要研究方向为快速成型。E-mail：792516984@qq.com