LFM信号参数估计误差分析及改进算法∗

孙文磊,常文革,闫飞飞

(国防科技大学电子科学与工程学院，湖南长沙410073)

0 引言

线性调频(LFM)信号因其大时宽带宽积的特性，可同时获得远的作用距离和高的距离分辨率，广泛应用于雷达、声纳、通信和电子侦察等领域[1-2]，其检测与参数估计是一个重要的研究课题。

目前，针对LFM信号检测与参数估计的算法，主要围绕估计性能或计算量两者之一，很少能兼顾两个方面。基于时频分析的方法中，短时傅里叶变换(STFT)计算量较小，但由于不确定性原理的制约，分辨率受限[3];LFM信号的 Wigner-Ville分布(WVD)为时频平面上一条直线，可利用Radon或Hough变换检测直线的特性估计参数(Radon-Wigner变换[4]、Radon-Ambiguity变换[5]和Wigner-Hough变换[6])，但其在信号的时频分布上作进一步处理，计算量仍然较大;分数阶傅里叶变换(FRFT)因其对LFM信号良好的聚集特性且其离散算法的计算量与FFT相当，广泛应用于对LFM信号的检测和分析[7-8]，然而其二维峰值的搜索过程导致计算量大，检测耗时长。为了提高算法的实时性，Peleg提出了离散多项式相位变换法(DPT算法)[9]，估计过程仅需两次FFT和两次一维搜索，运算量较小，但其在低信噪比条件下估计精度不高，而且当信号到达时间未知时，无法估计初始频率。

针对上述问题，本文采用DPT算法结合FRFT离散并行快速算法，实现LFM信号的实时高精度参数估计;深入研究了FRFT参数估计的误差来源，并提出了相应的改进算法;为进一步提高估计精度，对参数估计结果进行谱校正。仿真结果表明，本文算法对LFM信号参数估计精度高，性能接近CRLB，基本能够实现实时应用。

1 DFRFT的并行快速实现

信号x(t)旋转角度为α的FRFT定义为

式中，旋转角度α=pπ/2，p为FRFT的阶次，可为任意实数;F p[·]为FRFT算子符号;为FRFT的核函数。

实际工程应用中，信号均为离散值，故需要计算离散形式的FRFT(DFRFT)。文献[10]提出的分解型快速算法将FRFT分解为信号的卷积形式，其计算结果与连续FRFT输出接近，可利用FFT来实现，计算复杂度为O(NlogN)，得到了广泛使用。

其离散形式的表达式为[10]

由于处理过程中对输入信号进行两倍的内插，对输出结果也要进行两倍的抽取，所以，可以计算真正的输出值Xα(m/Δx)=Xα(2m/(2Δx))， 并 行 实 现 FRFT 的 快 速计算[10]。

文献[11]在分解型快速算法的基础上提出了一种并行快速算法(记为FRFT2)，算法效率加快了2～4倍，其离散表达式为

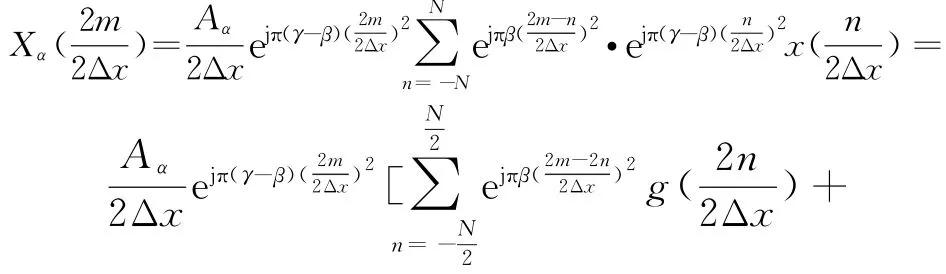
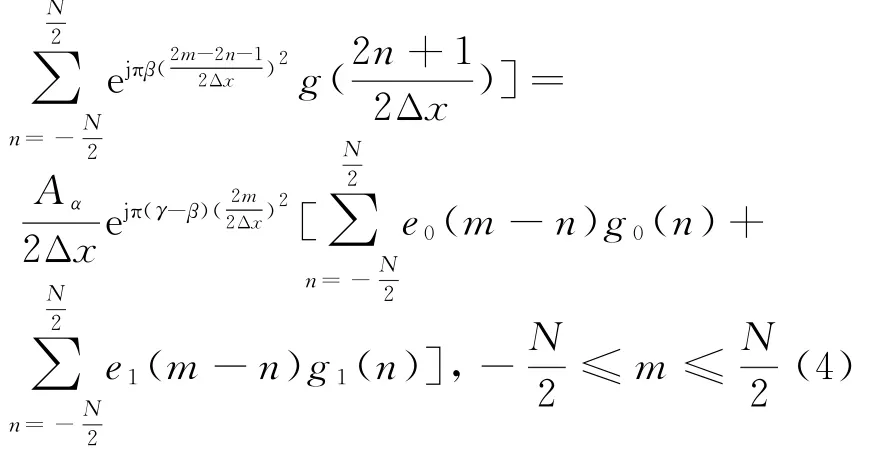
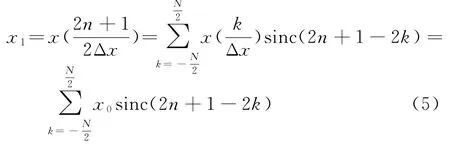
计算流程如图1所示。

图1 DFRFT的并行快速实现

2 基于FRFT的估计误差分析

2.1 FRFT域LFM信号的参数估计

含噪声的单分量LFM信号可表示为

式中，a0，φ0，f0，μ为未知参数;w(t)是方差为σ2w的加性高斯白噪声。

LFM信号检测估计过程可描述为[7]

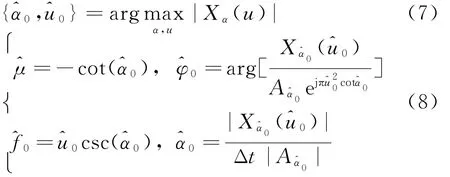
式(8)是对信号经过离散尺度化进行量纲归一化处理后得到的估计公式，实际工程应用中是对采样后的离散数据进行参数估计，中心频率和调频率的计算公式如式(9)所示:

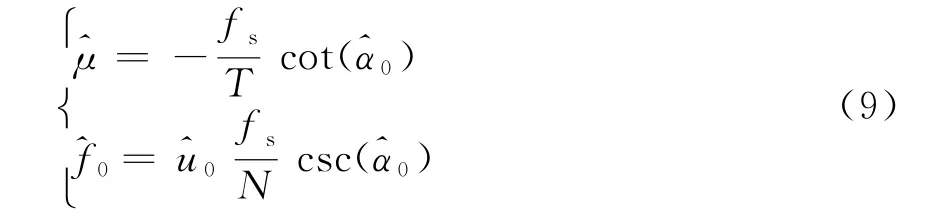
2.2 基于FRFT的估计误差分析

由2.1节可知，信号参数估计过程就是在(α，u)二维离散平面搜索峰值点，所得到的峰值点与真实峰值点之间存在的偏差即为参数估计误差。峰值点偏差是由信号噪声和离散分辨率两个因素造成的。由于噪声在(α，u)平面均匀分布，故(α，u)平面离散化是产生峰值点偏差的主要原因。

下面，从参数估计公式出发推导离散化对峰值点偏差的影响。(α，u)平面的离散变量为旋转角度α和FRFT域u，离散值分别由旋转角度搜索间隔π/m(m为搜索次数)和信号采样点数N决定。

当α0，u0为理论值时，满足

令Δf0和Δμ分别表示中心频率和调频率估计误差，则

(α，u)平面离散化引入的误差为

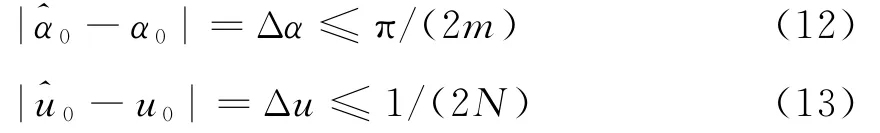
对于调频率误差Δμ，当Δα很小时

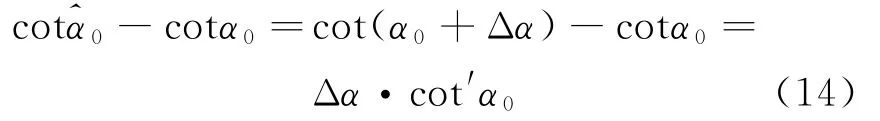
则调频率估计误差为

对于中心频率误差Δf0，当Δα很小时

As为内参物对照品s的峰面积，Cs为内参物对照品s的质量浓度，Ai为某待测成分对照品i的峰面积，Ci为某待测成分对照品i的质量浓度

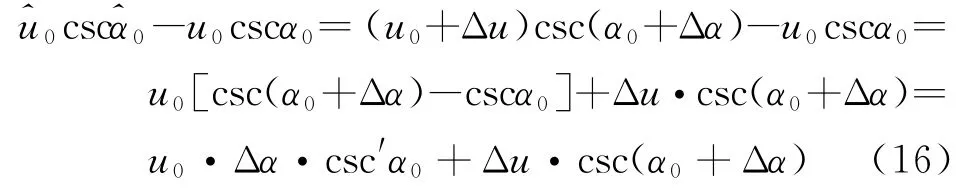
故中心频率估计误差为

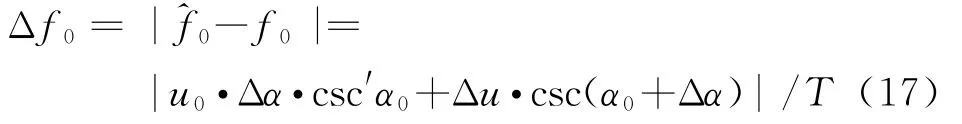
3 LFM快速估计改进算法

令Δμ1，Δμ2分别代表搜索间隔和采样率改变前后的调频率误差，分析它们对估计误差的影响。

① 当Δα减小n倍，N不变时

调频率误差减小n倍。

② 当N减小n倍，Δα不变时

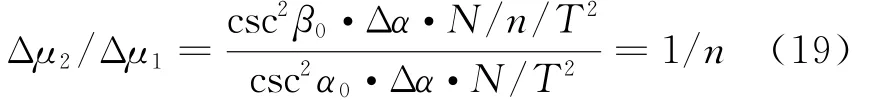
式中，β0为N改变后的最佳旋转角度，满足cotβ0=ncotα0，cotβ0斜 率 满 足 csc2β0≈n·α0/β0csc2α0。

由于α0=arccot(-μ·T2/N)，β0=arccot(-μ·T2/(N/n))，可得到-π/2＜α0＜β0＜0，又arccotx斜率为arc cot′(x)=-1/(1+x2)∈(-1，0)，则

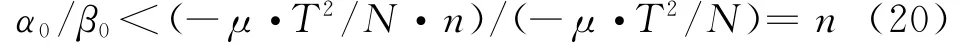
调频率误差增大，但增大倍数小于n倍。

③ 当Δα与N同时减小n倍时

综合①、②可知，

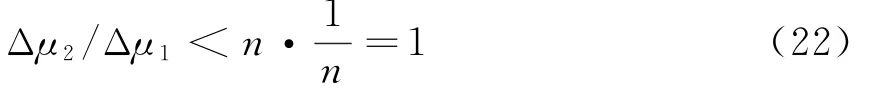
调频率误差始终是减小的。

计算量分析:

由上述分析可知，N的减小对计算量的减小的影响大于搜索间隔减小对计算量的增加，而搜索间隔减小对误差的影响大于N减小对误差的增加，所以选择减小采样点数N即欠采样[13]的同时减小相应搜索间隔来改进调频率估计的误差。这样，在减小计算量的同时也减小了误差。

对于中心频率误差Δf0，由于Δα很小且在接近π/2时斜率几乎为0(通常LFM信号的调频率很大，对应的旋转角度接近π/2)，中心频率误差可简化为

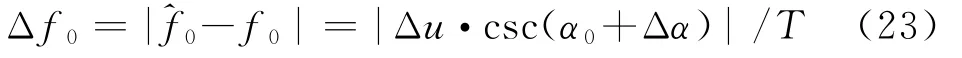
令Δf01，Δf02分别代表搜索间隔和采样率改变前后的中心频率误差，分析它们对估计误差的影响。

① 当Δα减小n倍，N不变时

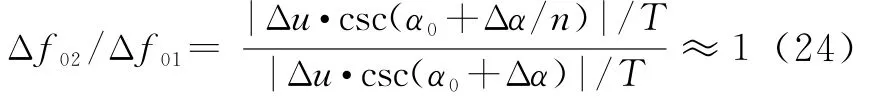
中心频率误差基本不变，计算量为O(mn/Nlog(N))，计算量增加n倍。

② 当N增大n倍，Δα不变时

中心频率误差减小n倍，但计算量为O(mn Nlog(nN))，计算量大大增加。

由上述分析可知，Δα的改变对中心频率误差影响不大;N的增加会减小Δu，从而减小中心频率误差，但两者都会大大增加计算量。所以，采用一种FRFT高分辨快速计算方法——Zoom-FRFT算法[14]，这种方法可在保持计算量不变的条件下，得到局部谱的精细结构，在N不变时，减小Δu，提高信号中心频率的估计精度。

与此同时，还可以先利用DPT算法[8]求出调频率的粗估值，确定调频率的搜索区间，保证搜索间隔不变的情况下，减小搜索次数，从而减小计算量;在每次FRFT计算中，采用FRFT并行快速算法FRFT2，提高搜索的效率;最后，对调频率和中心频率的估计值，还可以利用谱校正技术(能量重心法)[15]进一步提高估计的精度。

将本文参数估计算法主要步骤归纳如下:

步骤1 首先，采用DPT算法对LFM信号调频率μ进行粗估。

DPT算法[9]是将LFM信号序列进行延时相关运算

式中，φ=π(f0+μN/2)N-πμN2/4;ω′(n)，n=0，1，…，N/2为噪声。

由式(26)可知，y(n)是一个频率为μN/2的正弦波序列，对该序列作正弦波频率估计，求得估计频率，即可计算出调频率的粗估值

步骤2 利用FRFT2算法在DPT算法确定的搜索区间内对欠采样信号进行峰值点的搜索。

DPT算法进行FFT后最大谱线处对应的频率为，假设左右次谱线处对应的频率分别为f1，f2，真实频率f∈(f1，f2)，从而可得出，即实际调频率由得

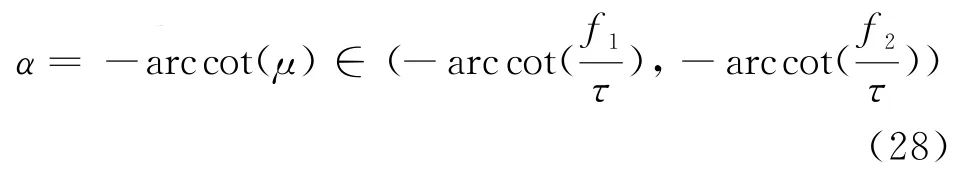
求二维平面峰值点的过程转化为在式(28)确定的区间内搜索最大值的过程:首先对信号进行欠采样处理(要求信号SNR＞-7 d B，欠采样倍数n≤6[14])，再采用FRFT2对欠采样的信号进行搜索。

步骤3 利用能量重心法精确估计调频率，得到最优旋转角度。

能量重心法是利用窗谱函数的能量重心位于坐标原点的原理对估计进行校正，频谱能量比较集中时，可以用主瓣内功率谱值较大的几条谱线作近似计算[15]，校正公式为

故对步骤2中欠采样信号在旋转角度区间内的FRFT2变换结果进行谱校正即可得到最优旋转角度，并计算出调频率估计值

步骤4 找到最优旋转角度后，对原始采样信号进行旋转角度为的Zoom-FRFT运算，得到FRFT域主瓣内谱线并进行谱校正，求出谱峰处的频率，最后根据

即可估计出中心频率。

4 仿真结果

为验证误差分析结论和改进算法性能，令信号样本长度N=1 000，信号参数分别为:幅度α0=1.0 V，初始相位φ0=0 rad，中心频率f0=0.09/TsHz，调频率μ=0.000 8/T2sHz/s，其中，Ts为采样间隔。

为验证利用DPT算法预估调频率再利用FRFT细搜和直接利用FRFT进行二维搜索的效率，在同等估计精度下所耗时间如表1所示。

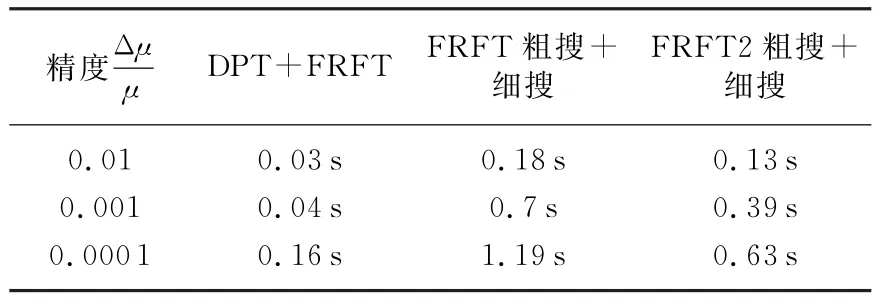
表1 不同算法在同等精度下耗时

表1说明采用DPT预估大大加快了参数估计的运算，且并行算法FRFT2的耗时优于FRFT，DPT+FRFT2算法基本能够实现参数的实时估计。

图2表示采样点数N和旋转角度搜索间隔π/m两个离散量对调频率估计误差的影响。从图2可以看出，只对信号进行欠采样而不改变搜索间隔会增加参数估计的误差;而在欠采样的同时减小相应搜索间隔就可以减小误差。

在上述仿真参数条件下，欠采样倍数为5时，欠采样前，估计耗时为0.15 s，欠采样后搜索间隔不变与搜索间隔减小两种情况下耗时分别为0.04 s和0.09 s，说明欠采样后减小相应搜索间隔在提高估计精度的同时也减小了计算量。

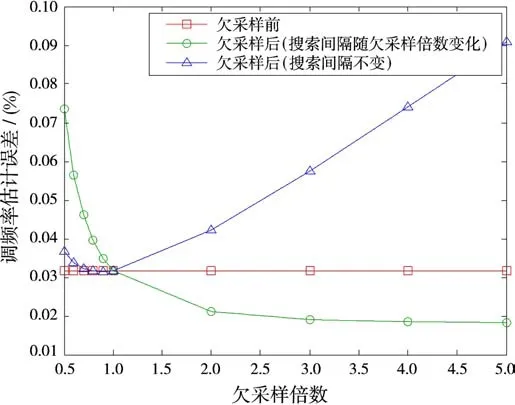
图2 调频率误差变化曲线

图3表示FRFT算法下采样点数N和旋转角度搜索间隔π/m两个离散量改变与Zoom-FRFT算法下离散量不变，中心频率估计误差的变化。从图3可以看出，对于中心频率，增加采样点数N相对于减小搜索间隔π/m对提高估计精度更为有效;而采用Zoom-FRFT算法，可以在离散量不变的同时提高中心频率估计精度，解决了计算量与精度的矛盾。

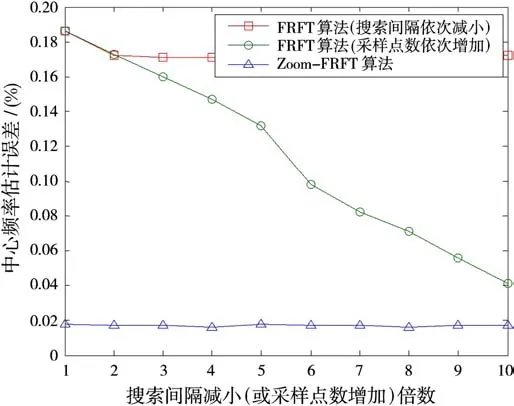
图3 中心频率误差变化曲线

图4显示了上述仿真参数下进行100次蒙特卡洛仿真，得到的在不同信噪比下，三种算法(FRFT[7]、FRFT谱校正[5]、本文算法)对信号中心频率以及调频率的均方误差(MSE)及其与CRLB的比较。

由图4可知，本文算法优于直接利用FRFT搜索的算法和一般的FRFT谱校正算法，其均方根误差非常接近CRLB，对调频率和中心频率改进的措施是有效的。同时，由表1可知，本文算法的估计耗时远小于FRFT的估计耗时，大大提高了算法的实时性，基本可以实现LFM信号参数的实时估计。但由于利用DPT算法进行预估，故本文算法只适合SNR大于-6 d B的情形。

图4 参数估计的均方误差随信噪比的变化曲线

5 结束语

本文通过分析研究调频率和中心频率的参数估计公式，得到采样点数N和旋转角度搜索间隔π/m对信号参数估计精度的不同影响，并根据结论提出了相应的改进算法:对于调频率的改进，提出了欠采样的同时减小相应搜索间隔的方法进行调频率的估计;对于中心频率的改进，采用Zoom-FRFT高分辨快速算法进行中心频率的估计。同时，为减小搜索的次数，采用DPT算法进行预估，为减小每次FRFT搜索的运算量，采用FRFT并行快速算法。最后，为进一步提高估计精度，对参数估计结果进行谱校正。仿真结果表明，此算法对LFM信号各项参数估计精度高，性能优于FRFT的谱校正算法，同时能够实现实时估计。然而本文算法只适用于单分量的LFM信号，多分量的LFM混合信号的实时高精度算法还需进一步研究。

[1]CHAN Y K，KOO V C.An Introduction to Synthetic Aperture Radar(SAR)[J].Progress in Electromagnetics Research B，2008(2):27-60.

[2]GUDRA T，HERMAN K.Some Problems of Analyzing Bio-Sonar Echolocation Signals Generated by Echolocating Animals Living in the Water and in the Air[J].Journal of the Acoustical Society of America，2008，123(5):3778-3783.

[3]YIN Qingbo，SHEN Liran，LU Mingyu，et al.Selection of Optimal Window Length Using STFT for Quantitative SNR Analysis of LFM Signal[J].Journal of Systems Engineering and Electronics，2013，24(1):26-35.

[4]许建忠，孙红伟，孙业岐，等.利用Radon-Wigner变换的LFM信号检测性能分析[J].河北大学学报(自然科学版)，2013，33(1):90-95.

[5]罗蓬，刘开华，黄翔东，等.高精度LFM信号参数估计的谱校正方法[J].系统工程与电子技术，2011，33(6):1237-1242.LUO Peng，LIU Kai-hua，HUANG Xiang-dong，et al.High-Accuracy Parameter Estimation for LFM Signals Based on Spectrum Correction[J].Systems Engineering and Electronics，2011，33(6):1237-1242.(in Chinese)

[6]张静，赵平平，贾佳，等.基于相对判决准则的LFM信号Wigner-Hough变换检测方法研究[J].西华大学学报(自然科学版)，2013，32(4):67-70.

[7]QI Lin，TAO Ran，ZHOU Siyong，et al.Detection and Parameter Estimation of Multicomponent LFM Signal Based on the Fractional Fourier Transform[J].Science in China Scr.F，2004，47(2):184-198.

[8]陈蓉，汪一鸣.基于FRFT的LFM脉压雷达移频干扰辨识[J].雷达科学与技术，2013，11(2):192-196.CHEN Rong，WANG Yi-ming.Detection of Frequency-Shifting Jamming to LFM Pulse-Compression Radar Based on FRFT[J].Radar Science and Technology，2013，11(2):192-196.(in Chinese)

[9]庞存锁.基于离散多项式相位变换和分数阶傅里叶变换的加速目标检测算法[J].电子学报，2012，40(1):184-188.PANG Cun-suo.An Accelerating Target Detection Algorithm Based on DPT and Fractional Fourier Transform[J].Acta Electronica Sinica，2012，40(1):184-188.(in Chinese)

[10]OZAKTAS H M，ARIKAN O，KUTAY M A，et al.Digital Computation of the Fractional Fourier Transform[J].IEEE Trans on Signal Processing，1996，44(9):2141-2150.

[11]TAO R，LIANG G，ZHAO X H.An Efficient FPGA-Based Implementation of Fractional Fourier Transform Algorithm[J].Journal of Signal Processing Systems，2010，60(1):47-58.

[12]卢慧英.分数阶傅里叶变换在信号分离及参数估计中的应用[D].苏州大学，2012.

[13]仇兆炀，陈蓉，汪一鸣.基于FRFT的线性调频信号欠采样快速检测方法[J].电子学报，2012，40(11):2165-2170.QIU Zhao-yang，CHEN Rong，WANG Yi-ming.Fast Detection of LFM Signal Based on FRFT and Sub-Nyquist Sampling[J].Acta Electronica Sinica，2012，40(11):2165-2170.(in Chinese)

[14]赵兴浩，陶然，邓兵，等.分数阶傅里叶变换的快速计算新方法[J].电子学报，2007，35(6):1089-1093.ZHAO Xing-hao，TAO Ran，DENG Bing，et al.New Methods for Fast Computation of Fractional Fourier Transform[J].Acta Electronica Sinica，2007，35(6):1089-1093.(in Chinese)

[15]丁康，郑春松，杨志坚.离散频谱能量重心法频率校正精度分析及改进[J].机械工程学报，2010，46(5):43-48.