正交频分LFM信号MIMO雷达的距离维高分辨∗

胡蜀徽,唐 佳,王志华,冉财章

(中国电子科技集团公司第二十九研究所,四川成都610036)

0 引言

MIMO雷达各天线阵元发射相互正交的线性调频信号,在空间叠加不能形成高增益波束,而是宽波束覆盖[1],在接收端通过匹配滤波处理来恢复发射信号分量,并通过DBF来形成同时数字多波束,覆盖发射波束区域。它具有抗截获性能高、弱目标检测能力强、距离分辨率高和空间搜索效率高[2]等特点,其信号模型及处理方式类似于步进频率雷达。步进频率雷达在不增加单通道发射带宽的前提下,通过脉冲间信号的合成来获得距离上的高分辨。MIMO雷达在兼顾前者优点的同时还能完成测速和相参积累功能。

步进频率雷达发射一串载频跳变的线性调频脉冲信号,然后再通过对脉冲回波进行匹配滤波和IFFT处理获得合成距离高分辨的效果。不同步进频率信号的参数选取会影响信号处理的方法,使得IFFT合成处理结果有一定冗余,从而造成目标距离走动并产生虚假目标。

MIMO雷达的处理方式是在数字下变频和匹配滤波后将各个发射信号分量进行相参合成,其信号处理过程包含了频谱拼接和相位补偿。合成后的一维距离像非常清晰,且副瓣很低,不会因为冗余造虚假目标,也不需要在距离上进行裁剪拼接。

1 MIMO雷达的信号模型及距离维高分辨合成方法

1.1 MIMO雷达的信号模型

设发射脉冲串数目为N,天线个数为M,各天线发射频率分量满足正交关系[3],间隔为fΔ,子脉冲宽度为Tp,脉冲重复周期为Tr,调频斜率μ=B/Tp,单个频点带宽为B,则接收到第i个重频的线性调频信号模型为

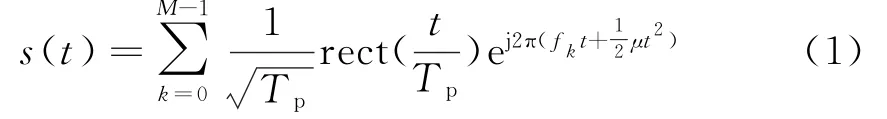
式中,rect(t/Tp)是宽度为Tp的矩形脉冲;f k是第k个信号分量的载频,f k=f0+kfΔ,f0为中频频率,两个不同频率的信号分量之间呈正交关系[4]。总带宽为Bs=B+(M-1)fp,信号的采样率为

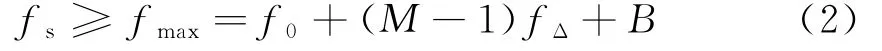
静止目标的雷达回波信号模型为

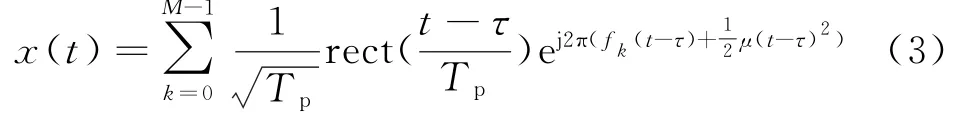
式中,τ=2R0/c,R0为该目标离雷达的视线距离。

1.2 匹配滤波处理

经过低通滤波器将全部频谱分量提取出来,然后进行数字下变频,得到

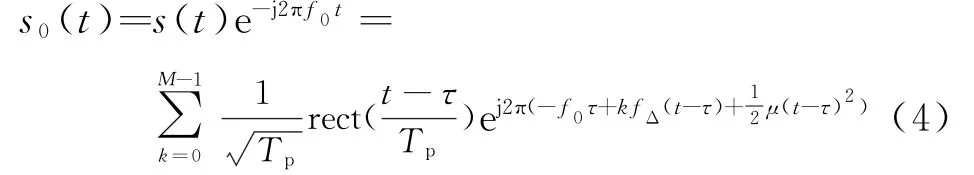
不同频率的匹配滤波信号模型为

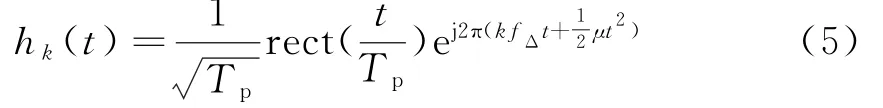
将数字下变频后的信号分别与不同频率的匹配滤波信号进行卷积,得到匹配滤波结果[5]。

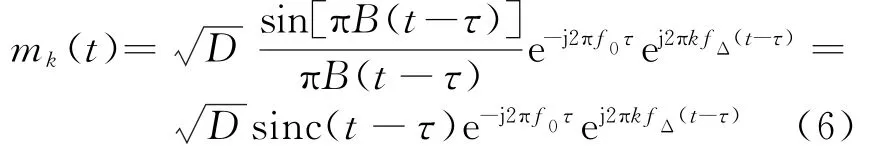
式中,D=BTp为时宽带宽积。

1.3 距离维高分辨合成处理

将不同频率的匹配滤波的信号直接相参合成[6],得到的信号为

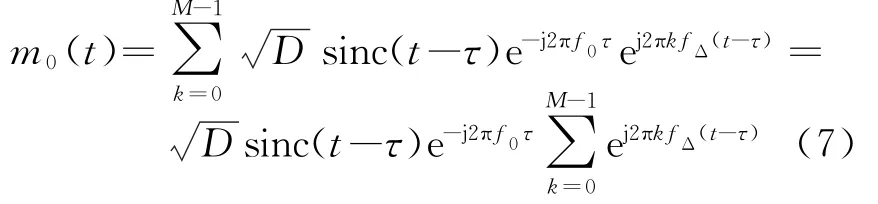
输出信号的带宽与匹配滤波器输入信号的带宽相等,为(M-1)fΔ+B。

利用等比数列求和公式：

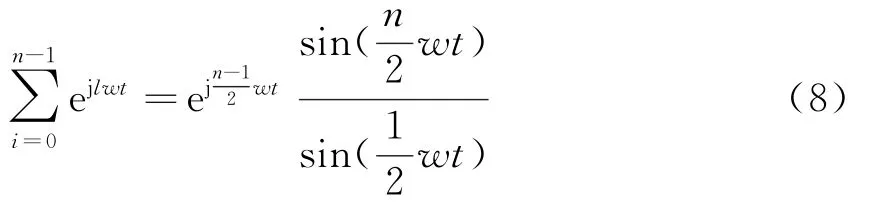
得到合成后的信号包络为

输出信号包络具有周期sinc函数的形式,输出脉冲宽度近似为发射信号带宽的倒数,即T o=1/[(M-1)fΔ+B]。因此,合成后的最小可分辨距离为

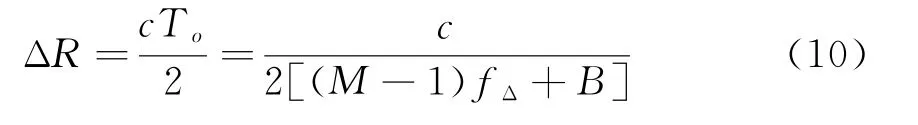
如果取fΔ=B,则距离分辨率为ΔR=c/(2MB),相对于单个频率的信号提高了M倍。

1.4 速度影响及消除方法

目标相对于雷达的径向速度是影响正交线性调频信号合成效果的一个重要因素,会引起目标峰值幅度降低,包络走动,旁瓣幅度升高,虚假目标出现,从而导致距离维高分辨效果变差[7]。

设目标的径向速度为v,则雷达回波的信号模型为

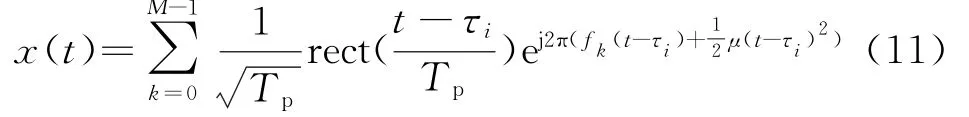
式中,τi=2(R0-iv Tr)/c,R0为该目标离雷达视线的距离,i为重频序号,fr为射频频率,fd为多普勒频率。

匹配滤波后信号的频域表达式为

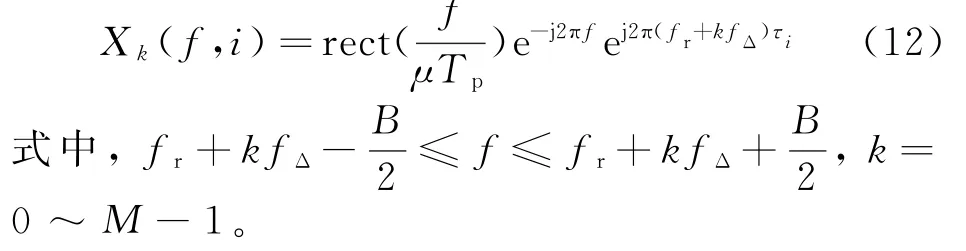
提取出对应的相位项,可以得到

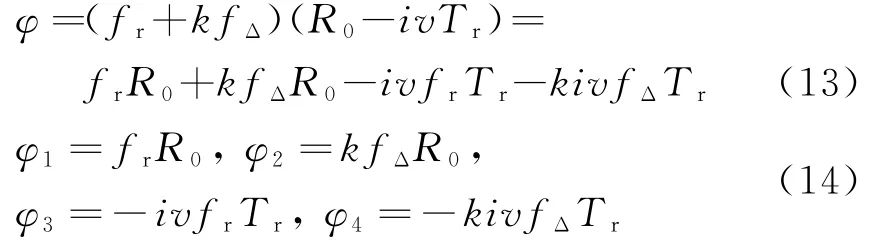
式中,φ1项为常数项,不会造成影响;φ2项为形成距离高分辨项的相位项;φ3项为各子脉冲间的多普勒项,在进行距离合成时,会降低目标的峰值,提高旁瓣的幅度,引起包络的走动,当运动参数较大时,将直接影响距离高分辨合成的效果;φ4项则会导致合成过后主瓣展宽。

因此,必须尽可能精确补偿速度,才能保证合成的效果。步进频率测速方法有频域互相关法、最小脉组误差法、最小脉组相位差分法和正负频率步进信号组合法等[8],但大多计算量过大,测速精度不高。而MIMO雷达不需要精确测速,只需对每个正交信号的脉冲串进行MTD处理,就可以补偿速度带来的相位项,然后再合成距离高分辨。

经过数字下变频和匹配滤波的结果为

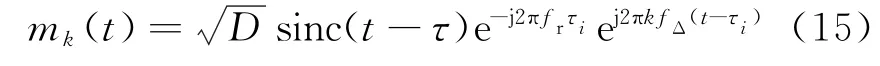
当积累时间不长的情况下,脉冲串之间的包络走动可以忽略,则可以得到

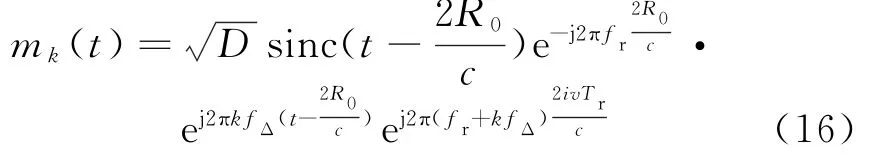
对每一个频率的脉冲信号进行MTD处理,重排后对距离单元作FFT变换,可得

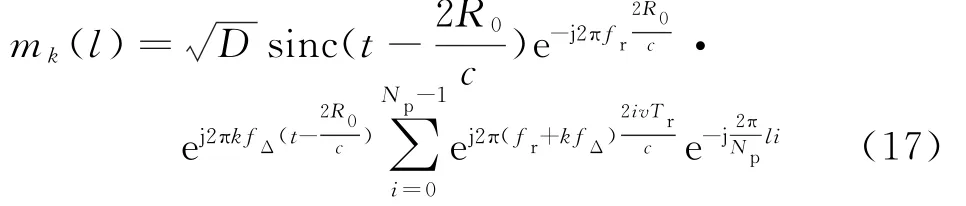
式中,Np为脉冲串个数,多普勒频率为fdk=2(fr+kfΔ)v/c。当合成后的相对带宽为窄带时,可以认为fdk相等。

当fdk=fr/Npl时,获得最大输出,为

速度引起的相位项被补偿,然后再进行相参合成,就可以实现距离维的高分辨。

MIMO雷达距离高分辨合成的信号处理流程如图1所示。

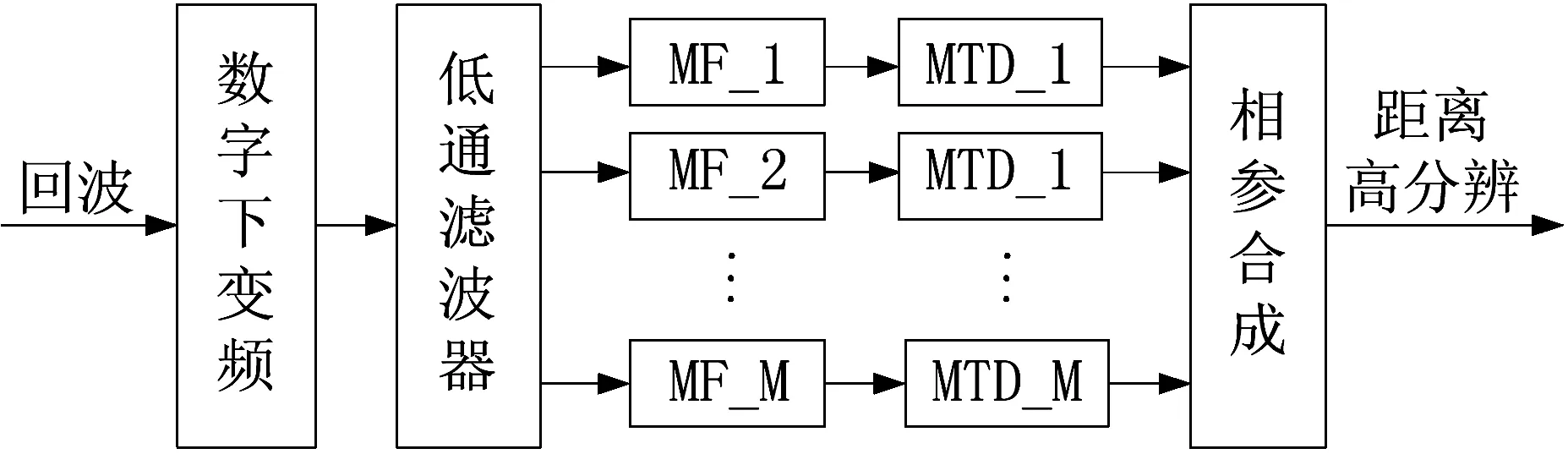
图1 距离高分辨信号处理流程图

2 仿真分析

根据上述理论分析,对基于4发4收的MIMO雷达进行仿真。仿真参数如下：设正交线性调频信号的起点频率f0=10 MHz,射频频率fr=10 GHz,采样频率fs=100 MHz,调频带宽B=3 MHz,频率间隔fΔ=3 MHz,脉冲宽度Tp=10μs,脉冲重复周期为100μs,脉冲个数为128。自相关结果如图2所示,不同频率信号之间的互相关结果如图3所示。

从图2可以得出,自相关的旁瓣电平为-13.7 dB。从图3可以看出,相邻两个信号存在一定互相关分量[9],互相关峰值幅度大小如表1所示。图3(a)、(d)及(f)中峰值约为-21 dB,其原因在于sinc函数旁瓣的影响[10]。

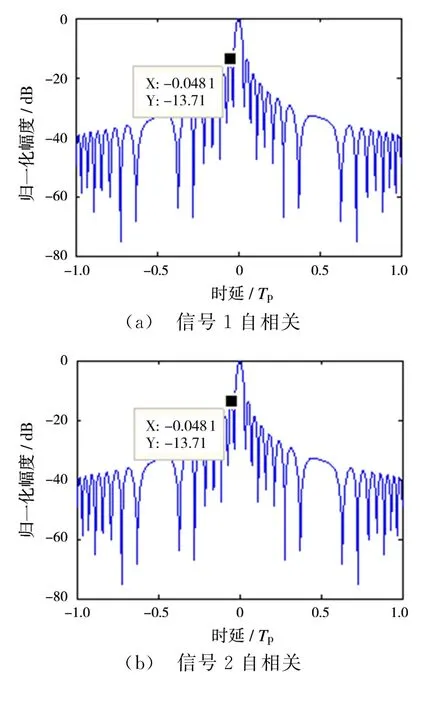
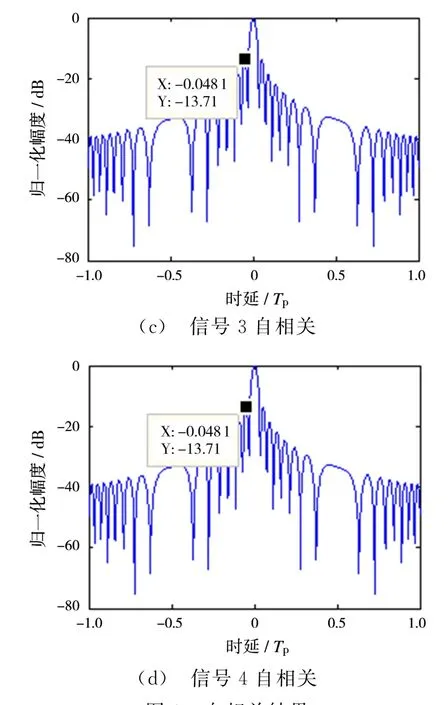
图2 自相关结果

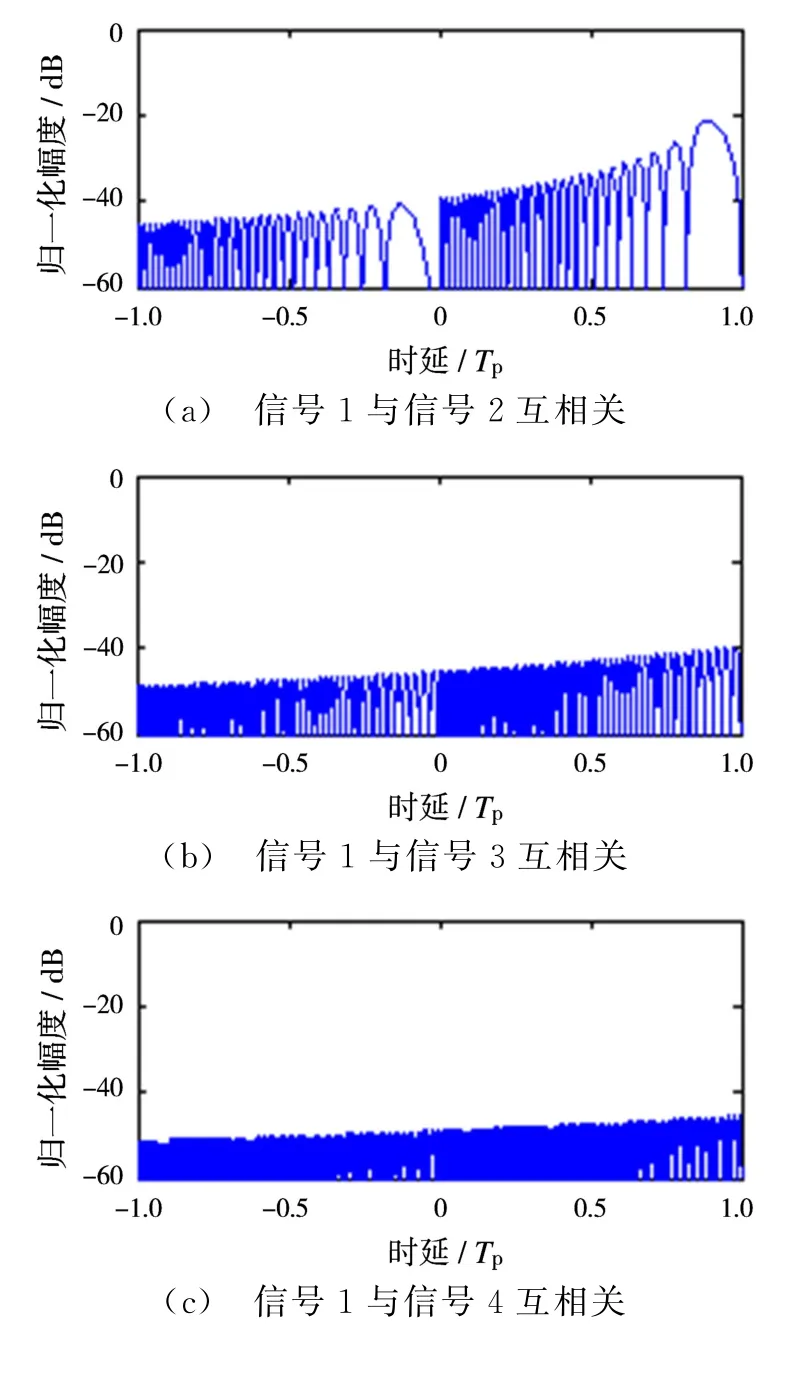
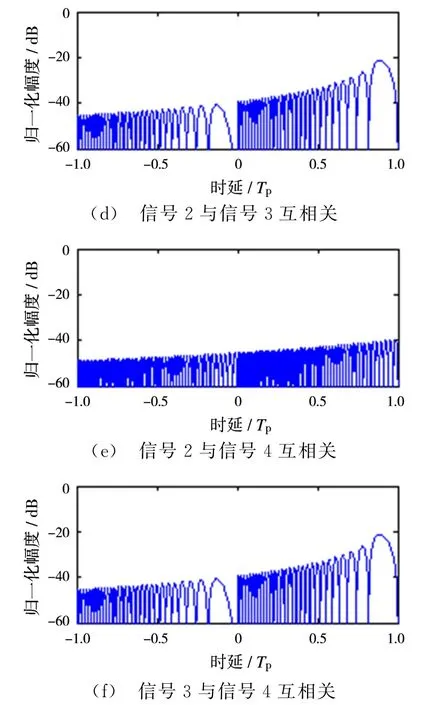
图3 不同频率信号间互相关结果

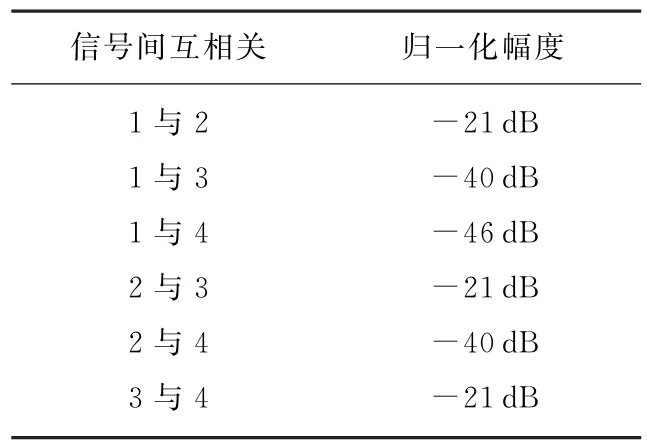
表1 信号互相关峰值幅度

设一目标距离为16 km,回波信号为所有发射信号分量之和。对接收信号进行匹配滤波的结果如图4所示。从图4可以看出,自相关旁瓣电平小于-13 dB,而互相关电平峰值小于-20 d B,互相关峰值的影响低于自相关峰值旁瓣,通过匹配滤波就可以分离出不同频率的线性调频信号。

设一目标距离为16 km,另一目标距离为16.035 km,合成处理前后的对比结果如图5所示。根据仿真参数,单个频率的线性调频信号的距离分辨率为50 m,合成后的距离分辨率为12.5 m,两个目标相差35m时,单个线性调频信号的距离分辨率无法分辨,而合成后两目标凹点的幅度为-16.94 dB,低于旁瓣峰值-13.7 dB,能够清晰地分辨出两个目标。

图4 不同频率的匹配滤波输出

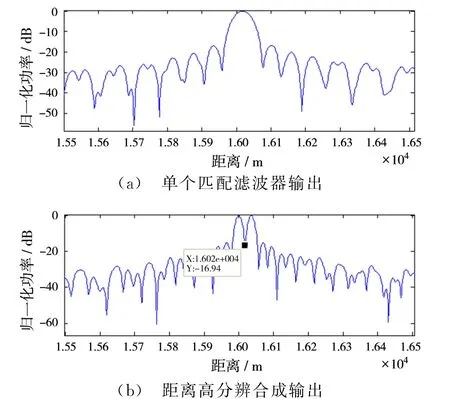
图5 合成前后匹配滤波器输出

不同速度条件下的合成处理结果如图6所示,随着速度的增加,旁瓣峰值升高,目标峰值降低。当速度从200 m/s增加到800 m/s时,旁瓣峰值从-12.38 dB上升到-4.93 dB,目标峰值从-1.22 dB下降到-5.88 dB,目标已经不能正确检测,而且还会出现虚假目标,距离维上目标峰值所在位置也出现了走动。

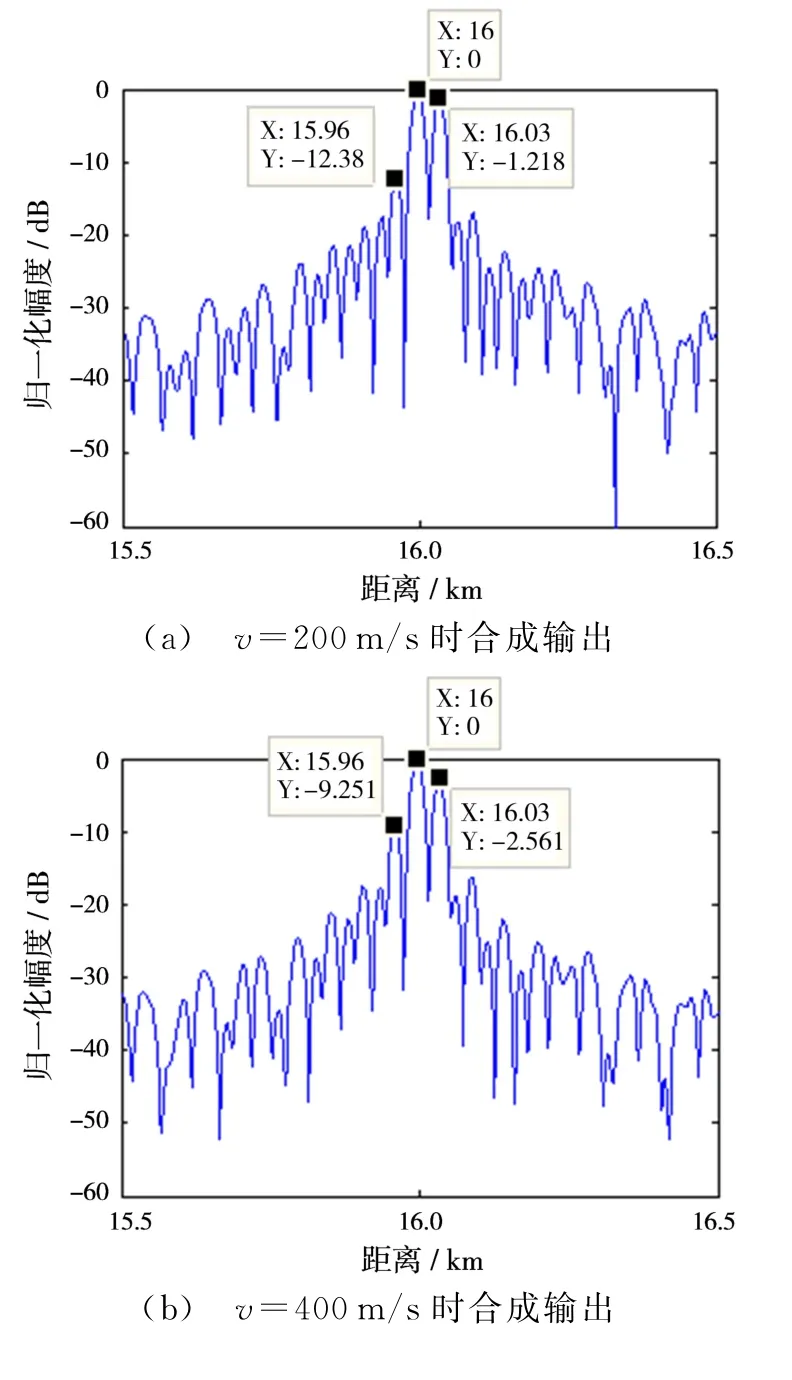
图6 速度对合成效果的影响

对不同速度条件下的线性调频脉冲串进行MTD处理,补偿速度引起的相位项,然后再进行相参合成处理,距离高分辨的合成结果如图7所示。可以看出,速度引起的相位项的影响已经消除,不同速度条件下旁瓣和目标峰值与速度为0时一致,能够正确检测出两个目标。

3 结束语

首先给出了MIMO雷达的信号模型和处理方法,分析了OFD-LFM信号的自相关函数和互相关函数,其特点是利用频率之间的正交特性,通过匹配滤波分离出不同频率的信号分量,然后相参合成实现距离维的高分辨。同时还分析了速度对合成效果的影响,以及通过MTD处理补偿速度引起的相位项消除速度影响的方法。该合成方法计算量较小、易实现,相比步进频率雷达需在距离上去冗余和测得速度后进行速度补偿的处理方式更具优势,有利于工程应用。

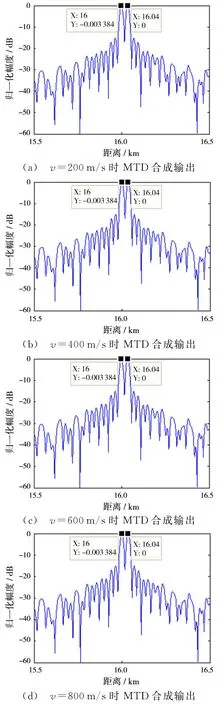
图7 MTD后的合成效果

[1]FISHLER E,HAIMOVICH A,BLUM R,et al.MIMO Radar：an Idea Whose Time Has Come[C]∥Pro-ceedings of the IEEE International Conference on Radar,Philadelphia：IEEE Signal Processing Society,2004：71-78.

[2]何子述,韩春林,刘波.MIMO雷达概念及其技术特点分析[J].电子学报,2005,33(12A)：2441-2445.

[3]李宏伟.MIMO雷达波形设计方法综述[J].现代雷达,2013,35(6)：12-14.

[4]陈正辉,严济鸿,何子述.MIMO雷达OFDM-LFM波形设计与实现[J].雷达科学与技术,2013,11(1)：77-81,86.CHEN Zheng-hui,YAN Ji-hong,HE Zi-shu.Design for MIMO Radar and Implementation of OFDM-LFM Waveform[J].Radar Science and Technology,2013,11(1)：77-81,86.(in Chinese)

[5]陈正中,李小波,梁浩,等.正交频分LFM信号的MIMO雷达的匹配滤波技术[J].雷达科学与技术,2013,11(2)：197-202.CHEN Zheng-zhong,LI Xiao-bo,LIANG Hao,et al.Matched Filtering Technology for MIMO Radar with OFD-LFM Signal[J].Radar Science and Technology,2013,11(2)：197-202.(in Chinese)

[6]裴英,肖文书.相干MIMO雷达关键技术研究[J].现代雷达,2013,35(3)：9-12.

[7]丁海林,李亚超,高昭昭,等.线性调频步进信号的三种合成方法的对比与分析[J].火控雷达技术,2007,36(4)：10-16.

[8]曹宇飞,屈晓光,黄培康.一种快速有效的步进频率测速方法[J].现代防御技术,2009,37(1)：80-82.

[9]刘波,何子述,王海江.MIMO雷达中的DFCW设计及性能分析[J].电子科技大学学报,2010,39(5)：688-691.

[10]施祥同,王虎,陈建军,等.OFDM雷达信号的宽带模糊函数性能分析[J].雷达科学与技术,2010,8(6)：554-558.SHI Xiang-tong,WANG Hu,CHEN Jian-jun,et al.Wideband Ambiguity Function of OFDM Radar Signal[J].Radar Science and Technology,2010,8(6)：554-558.(in Chinese)