一种改进的天波雷达海杂波循环对消算法∗

林志榕,胡进峰,李 强,李会勇,李 军

(1.电子科技大学电子工程学院,四川成都611731;2.九江职业技术学院,江西九江332007)

0 引言

天波超视距(over-the-horizon,OTH)雷达工作于高频段(3～30 MHz),利用电离层的反射对目标进行下视探测,不受地球曲率影响,探测范围达到数千公里,能够对弹道导弹、大型海面目标和隐身飞机实现早期预警,具有重要的战略意义[1-6]。

舰船等慢速目标的检测一直是天波雷达的难点之一。由于舰船航速较慢,其多普勒频率靠近强大的海杂波,目标频谱容易被掩盖,因此检测起来十分困难[3-4]。而且,为了增加雷达的重访率,提高数据率,降低电离层扰动等因素的影响,一般需要在短相干积累条件下检测舰船目标[4],然而短相干积累会导致雷达回波频谱的多普勒分辨率降低,进一步增加了目标检测的难度。

实现短相干积累条件下的舰船检测,目前主要方法是美国天波雷达中实际使用的海杂波循环对消法[7],该方法是在舰船检测前,直接利用傅里叶谱分析估计杂波分量的参数,然后重构杂波信号,通过循环迭代的方法在时域上依次将海杂波的峰值减去。此外还有子空间投影算法[6,8-9],该方法根据海杂波和舰船目标在子空间的聚集特性来进行杂波抑制,然而短相干积累条件下,有限的数据会导致子空间估计精度不高,导致海杂波泄露到目标子空间,从而降低海杂波抑制性能。而且,海态情况不平稳时,相邻距离单元和方位单元之间的相关性会降低,严重影响舰船目标的检测[6]。因此,短相干积累条件下,一般采用海杂波循环对消法来进行杂波抑制。

本文注意到,传统的循环对消法通常会有较强的海杂波残留,其原因在于短相干积累条件下,序列的长度很短,仅利用傅里叶谱分析不能够提供足够高的多普勒分辨率,使得传统的循环对消方法难以准确估计海杂波的频率,因而不能有效抑制海杂波。文献[7]所提的海杂波循环对消法通过搜索频谱最大峰值来估计杂波参数,但由于短相干积累和栅栏效应,海杂波信号真实频率的位置可能落于主瓣内2根谱线之间,导致估计精度不高,进一步影响相位和幅度等参数的估计精度。

基于上述考虑,本文提出一种改进的循环对消海杂波抑制算法。该算法首先在短相干积累条件下,利用最大的3根谱线来估计海杂波信号的频偏,然后用估计的频偏来对粗估计得到的频率进行校正,提高了海杂波频率的估计精度。在此基础上,对时域的海杂波信号进行精确估计,并从原始回波信号中减去,从而抑制杂波;此外,本文注意到天波雷达海杂波频率通常只在一定的范围内变化,因此本文进一步给出了海杂波频率变化的界限,在该界限内对海杂波进行估计和消除,可以避免目标信号被误认为剩余杂波而被对消掉。仿真结果表明,在同样的海杂波背景下,与传统的海杂波循环对消法相比,本文算法能够用更少的对消次数得到更优的效果,剩余杂波能量更低,具有更加良好的杂波对消性能。

1 天波雷达回波信号模型

OTHR的回波信号x(t)如下：

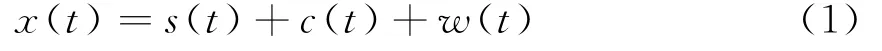
式中,s(t)为目标的回波信号,c(t)为海杂波信号,w(t)为加性的高斯白噪声信号。

海杂波信号c(t)由海面回波多普勒谱中的一阶谱和高阶谱构成,一般只考虑一阶谱和二阶谱,其中一阶谱在频谱中体现为两个关于零频率点对称的尖峰,即Bragg峰,Bragg峰对应的多普勒频率称之为Bragg频率,它与雷达工作频率的关系[1-2]为

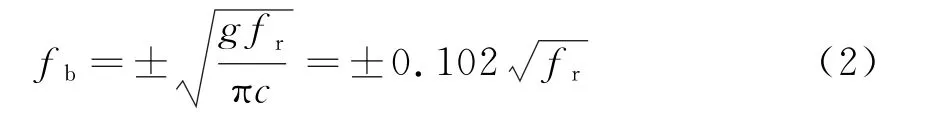
式中,fb为Bragg频率,±分别表示海浪运动方向朝向或背离雷达,fr为雷达的工作频率,g为重力加速度,c为光速。两个Bragg峰附近一定范围的海洋回波多普勒谱为二阶谱,相对于Bragg峰来说,能量较低,可以建模为高斯白噪声。因此,可以得到杂波分量的模型为

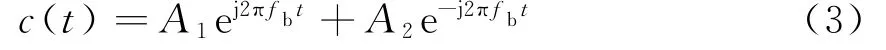
式中,A i(i=1,2)表示Bragg峰的幅度。

一般来说,舰船的运动速度比较慢,在短相干积累时间内可以看作保持匀速运动,因此舰船的雷达回波信号可以建模成正弦信号。舰船速度一般低于20 m/s,其产生的多普勒频率靠近强大的海杂波Bragg峰,舰船目标容易被掩盖,给目标检测带来不利影响[2,4]。因此,在进行慢速舰船目标检测前,必须先抑制一阶海杂波。

2 所提改进的循环对消海杂波抑制算法

本文注意到,文献[7]所提的海杂波循环对消法的性能取决于杂波参数的估计精度,但实战要求天波雷达工作于短相干积累条件,在短相干积累下,短时间序列的频率分辨率较低,利用传统的Fourier谱来估计杂波参数无法满足精度要求,杂波剩余在回波多普勒频谱中比较严重,会造成虚警概率的增加,而且随着对消次数的增加,算法实时性也会受到影响,不利于舰船目标的检测。

针对上述问题,本节给出了一种改进的循环对消海杂波抑制算法,该方法首先利用傅里叶变换后最大谱线位置得到海杂波频率的粗估计,然后用最大的3根谱线进行插值估计频偏,从而利用频偏来对粗估计得到的频率进行校正,得到海杂波频率的高精度估计。该算法计算量小,估计精度高,能够对杂波参数进行精确估计,在此基础上对时域的海杂波信号进行精确估计,并从原始回波信号中减去,实现杂波抑制。

2.1 海杂波频率的粗估计

在式(1)中,海杂波c(t)通常很强,相比之下,目标信号s(t)能量很弱,而且目标信号和海杂波信号的主要成分都是复正弦信号,可以将目标信号合并写成海杂波信号c(t)。因此,式(1)的离散形式可以近似写成

式中,强的海杂波信号c(n)的主要成分是复正弦信号,海杂波的二阶谱和高阶谱成分可近似成白噪声,因此式(4)可以近似写成

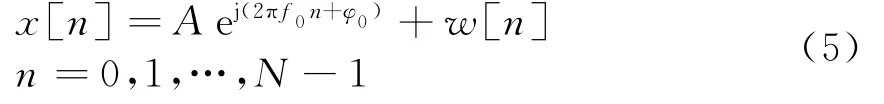
式中,A,f0,φ0分别为强海杂波分量的幅度、频率和初相,N为样本数,w[n]为零均值复高斯白噪声,方差为σ2。

对x(n)进行离散傅里叶变换,可得

式中,W(k)为高斯白噪声w(n)的DFT。傅里叶变换后最大谱线对应的频率即粗估计得到的频率。

文献[7]就是用这种方法进行频率估计的,该方法估计得到的频率与实际频率之间存在偏差,造成参数估计精度不高,影响杂波对消性能。

2.2 海杂波频偏的估计

由于离散谱存在“栅栏”效应,实际的频率中心与最大谱线位置对应的频率是有偏差的,文献[7]中没有考虑这种偏差,导致海杂波频率估计不准确,进一步影响幅度和相位的估计精度,从而造成杂波对消性能下降,残留杂波严重。考虑到这一点,本节给出了一种估计频偏的方法,然后利用频偏对频率进行校正。

这里我们用k p表示最大谱线在频谱中对应的位置,可得到粗估计的频率f p=k p/N,δ代表信号真实频率与粗估计得到的频率的相对偏差,变化范围为|δ|＜0.5,于是式(5)中海杂波信号的真实频率可表示为

这样,信号的真实频率估计就转换为δ的估计问题了。

最大谱线位置k p与其左右相邻谱线位置k p-1、k p+1处的离散傅里叶变换可表示为

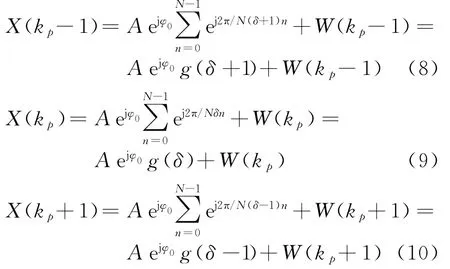
式中,函数g(·)定义如下：

对g(δ)进行泰勒展开,只保留δ的一次项,可得

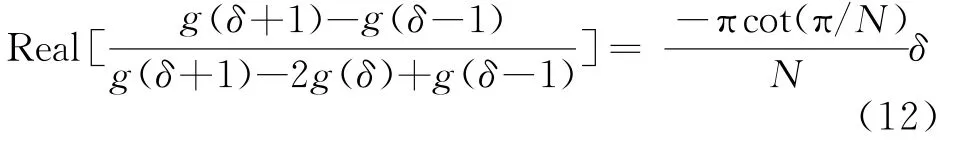
当信噪比较高时,分别用X(k p-1)、X(k p)、X(k p+1)代 替Aejφ0g(δ+1)、Aejφ0g(δ)、Aejφ0g(δ-1),从而得到δ的估计值：

2.3 频率校正与时域海杂波估计

为了提高估计精度,通过一个简单的误差消除函数,可以得到误差消除后的估计值：

因此,通过式(7)可以得到信号频率的估计值0：

通过以上推导,便可以精确估计杂波分量的频率,幅度则从频谱峰值得到,初始相位则通过最小化剩余能量来求得,即

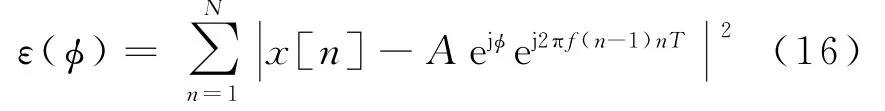
式中,x[n]为回波信号,N为回波序列的长度,f,A,φ分别为该分量的多普勒频率、幅度和初始相位,T为脉冲重复周期。

2.4 海杂波频率界限与算法流程

该算法需要循环迭代地进行,通过海杂波频率的高精度估计算法获得最强分量的参数后,重构出该分量的时域信号,然后从剩余回波中减去。

一般来说,海杂波的一阶谱和二阶谱的频率变化范围为-2fb～2fb,在此范围之内的杂波信号能量比较强,因此,可以通过设置一个杂波界限来定义需要对消的杂波,从而便于程序自动搜索和识别舰船目标。

迭代次数通过设置的杂波界限来确定,在循环过程中,在Bragg峰周围定义一个杂波界限,在该范围之内的峰值信号视为杂波,算法只在该范围内进行,只要估计得到的频率跳出该杂波界限,算法终止,从而避免将范围之外的舰船目标误认为剩余杂波而一起对消掉。具体算法流程如图1所示。

设原始回波信号为x[n],n=1,2,…,N,经过循环对消后的信号为x k(n),k是循环对消的次数。算法的具体步骤如下：

(1)初始化,令k=0,x k(n)=x(n)。

(2)对剩余回波信号x k(n)作FFT,如果是第一次循环,则该回波信号为该距离单元的原始回波。

图1 本文所提海杂波抑制算法流程

(3)采用海杂波频率的高精度估计算法,估计当前最强的杂波分量对应的多普勒频率f t,信号幅度A则可以通过搜索频谱峰值得到。

(4)通过式(16)最小化剩余功率,估计该分量的初始相位φ,从而该分量信号可以重构为

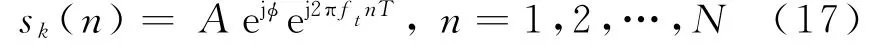
式中,T为脉冲重复周期,N为积累的脉冲数。

(5)将该重构的最强杂波分量从时域回波信号中减去,得到了第k+1次对消的剩余回波,剩余回波可以写为

(6)判断步骤(3)估计的频率是否在杂波界限内,如果是,继续从步骤(2)执行,如果不是,则算法停止迭代,输出处理后回波的频谱,此时频谱中的明显尖峰便是舰船目标。

3 仿真结果与分析

本节将分别给出本文所提改进的循环对消海杂波抑制算法和文献[7]所提海杂波循环对消法对天波雷达回波信号的仿真结果,对比分析仿真性能,并对实测数据进行处理,处理结果表明,本文所提算法能用更少的对消次数凸显出舰船目标,而且残留杂波能量更低。

3.1 模拟数据仿真结果与分析

仿真条件：雷达工作频率为10 M Hz,以低入射角照射在海面上(θ→0),则Bragg频率为fb=0.322 6 Hz,正负Bragg峰的幅度之比为3∶2。脉冲重复频率为40 Hz,发射256个脉冲,则其相干积累时间为6.4 s,属于短相干积累范畴,杂噪比为30 dB。设只有一个慢速舰船目标,信噪比为-5 d B,速度v=12 m/s,对应的多普勒频率fd=0.8 Hz。

仿真结果如图2～4所示。其中图2给出了添加目标的天波雷达回波谱,目标位置已在频谱中标记出来,可以看出,慢速舰船目标淹没在强大的海杂波一阶谱峰中。

图2 天波雷达回波谱

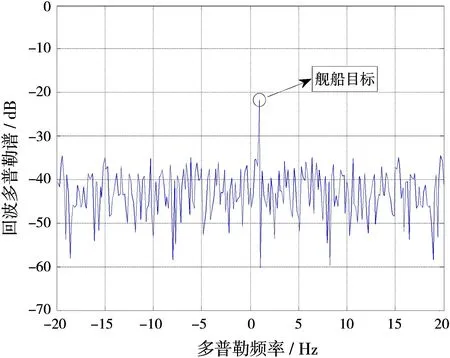
图3 本文算法2次对消后的结果

图4 两种算法经过2次对消后的结果

为了方便目标检测,用本文算法进行杂波对消处理,提高信杂比。图3给出了本文算法进行2次杂波对消后的频谱。可以看出,两个Bragg峰均被对消掉了,几乎没有剩余杂波,目标被分离出来,频谱上有一个明显的尖峰,这便是舰船目标。该结果证明算法具有很好的杂波对消性能。在对消过程中,使用杂波界限来控制对消次数,杂波对消只在所定义的杂波界限中进行,但是界限的选择需要谨慎,一般通过经验选取。

为了和文献[7]所提的海杂波循环对消法进行对比,图4给出了两种算法经过2次杂波对消后的频谱。可以看出,经文献[7]提出的循环对消算法处理后,海杂波剩余较为严重,目标并没有分离出来,仍然被海杂波一阶谱所掩盖;相比之下,本文算法由于参数估计更为精确,处理之后,杂波几乎没有剩余,目标在频谱中清晰可见,出现明显尖峰。因此,本文算法具有更良好的杂波对消性能。

3.2 实测数据验证

实测数据长度为512个点,CIT约为6.14 s,雷达工作频率为18.3 MHz。由于目前实测的舰船数据较少,在实测海杂波背景下,添加一个慢速舰船目标,其速度v=12 m/s,对应多普勒频率为0.8 Hz。原始回波信号多普勒谱如图5所示,目标被强大的一阶海杂波所遮盖,难以进行检测。本文算法处理结果如图6(a)所示,图6(b)是算法有效部分的局部放大图。在实测数据的处理中,同样使用杂波界限,杂波对消只在所定义的范围中进行,避免舰船目标被误认为剩余杂波而被对消掉。从图中可以发现,经过本文算法对消后,杂波得到一定的抑制,幅度下降约20 dB,虽然杂波还有部分剩余,不过慢速目标已经分离出来,可以对其进行检测。为了对比本文算法和文献[7]的海杂波循环对消法的性能,图7(a)给出了两种算法经过11次对消后的频谱,图7(b)是其在[-1,+1]Hz频率之间的局部放大图。从图中可以看出,本文算法对于杂波的对消性能要优于文献[7]所提算法,剩余杂波能量较低,慢速目标可以分离出来,提高目标检测效能。

图5 天波雷达回波谱

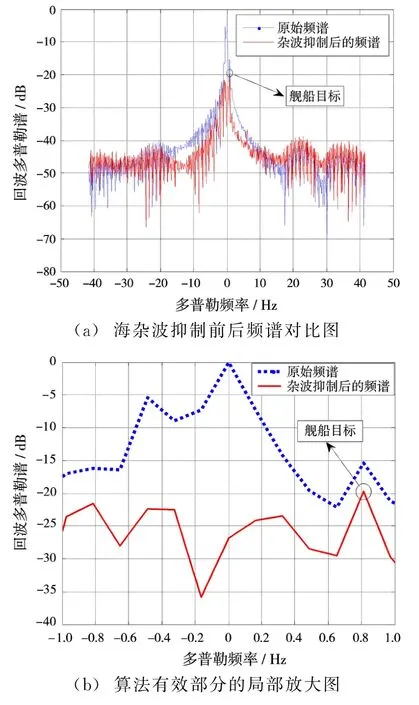
图6 采用本文海杂波抑制算法前后频谱对比图

图7 传统算法和本文算法杂波抑制效果对比

4 结束语

针对传统循环对消法对海杂波参数估计精度不高这个问题,本文提出了一种改进的循环对消海杂波抑制算法,该方法利用最大的3根谱线来估计频率,计算简单,估计精度高,能够对回波中各个正弦分量的频率、幅度、初相位进行精确估计,从而降低了剩余杂波能量。此外,使用杂波界限可以避免目标信号被误认为剩余杂波而被对消掉,进一步提高了目标检测性能。由仿真结果可以得到,本文算法能够用更少的对消次数凸显出舰船目标,而且剩余杂波能量更低,具有更良好的杂波对消性能。最后,实测数据的处理结果也检验了该算法的有效性。

[1]许丁文,李会勇,胡进峰,等.天波雷达电离层污染校正与海杂波抑制[J].雷达科学与技术,2012,10(6)：639-644.

[2]戴文娟,胡进峰,肖赛军,等.基于遗传算法的OTHR机动弱目标检测[J].雷达科学与技术,2013,11(1)：59-64.

[3]罗欢,陈建文,赵志国,等.基于信号阻塞矩阵检测OTHR舰船目标[J].雷达科学与技术,2011,9(2)：160-165.

[4]郭欣,倪晋麟,刘国岁.短相干积累条件下天波超视距雷达的舰船检测[J].电子与信息学报,2004,26(4)：613-618.

[5]赵志国,陈建文,鲍拯.一种改进的OTHR自适应海杂波抑制方法[J].系统工程与电子技术,2012,34(5)：909-914.

[6]赵志国,陈建文,鲍拯,等.OTHR海杂波抑制典型方法综合性能评估[J].武汉理工大学学报(交通科学与工程版),2012,36(6)：1270-1274.

[7]ROOT B T.HF-Over-the-Horizon Radar Ship Detection with Short Dwells Using Clutter Cancellation[J].Radio Science,1998,33(4)：1095-1111.

[8]WANG G,XIA X G,ROOT B T,et al.Manoeuvring Target Detection in Over-the-Horizon Radar Using Adaptive Clutter Rejection and Adaptive Chirplet Transform[J].IEE Radar,Sonar,and Navigation,2003,150(4)：292-298.

[9]MARTIN W Y,KHAN R,SON L N.A Singular Value Decomposition(SVD)Based Method for Suppressing Ocean Clutter in High Frequency Radar[J].IEEE Trans on Signal Processing,1993,41(3)：1421-1425.

[10]CANDAN C.A Method for Fine Resolution Frequency Estimation from Three DFT Samples[J].IEEE Signal Processing Letters,2011,18(6)：351-354.

[11]CANDAN C.Analysis and Further Improvement of Fine Resolution Frequency Estimation Method from Three DFT Samples[J].IEEE Signal Processing Letters,2013,20(9)：913-916.