股指期货套期保值效率比较研究——基于沪深300股指期货与新华富时A5指数期货

范泰奇，韩复龄

（中央财经大学金融学院，北京 100081）

股指期货套期保值效率比较研究
——基于沪深300股指期货与新华富时A5指数期货

范泰奇，韩复龄

（中央财经大学金融学院，北京 100081）

文章基于我国股票型基金十大重仓股构建投资组合，并利用沪深300股指期货与新华富时A50指数期货的日数据对这两种股指期货的套期保值效率进行比较研究，以探究两者在套期保值效率上的差异和造成差异产生的原因。在利用OLS、VECM和ECM-BGRACH等静态和动态套期保值模型和基于风险最小化的套期保值绩效指标对沪深300股指期货与新华富时A50指数期货的套期保值效率进行研究后发现，在静态最优套保比、时变最优套保比和套期保值绩效指标的比较中，新华富时A50指数期货都要优于沪深300股指期货。这种套期保值效率上的差异主要来自于两个金融工具间的合约与交易规则的差别。建议通过设立适当时间的晚间电子盘交易，并允许金融机构在规定的份额内进行期指套利交易，以提升沪深300股指期货在套期保值市场功能上的效率。

股指期货；套期保值；金融工具；金融投资

一、引言

沪深300股指期货和新华富时A50指数期货是目前全球市场上仅有的两只跟踪中国A股市场的金融衍生产品。前者成立于2010年4月16日，而后者的成立时间更早，自2006年9月5日开始已经在新加坡证券交易所上市交易。在沪深300股指期货成立之前，新华富时A50指数期货是全球市场上仅有的可以通过套期保值的操作方式对冲A股市场系统性风险的金融工具。但由于交易规则缺陷以及后来沪深300股指期货上市的替代效用影响，新华富时A50指数期货便日渐遭遇冷遇，成交量不断萎缩，作为风险对冲工具的作用也日渐式微。相反日渐成熟且具有期限价格拟合度较好、基差较小、交割日市场波动正常等良好特征的沪深300股指期货作为套期保值工具对冲A股市场系统性风险的效果越来越好。但在交易规则上沪深300股指期货也存在局限性，例如对于QFII的股指期货额度限制，只允许金融机构利用股指期货进行套期保值即卖空股指期货而不能进行套利等买入股指期货的操作等。这些局限性限制随着股指期货的不断发展开始逐渐影响了沪深300股指期货同沪深300指数间的拟合效果，间接影响了沪深300股指期货作为套期保值工具的效用。而新华富时A50指数期货确没有这些限制，且从2010年8月23日开始改革了合约规则，新的规则显著缩小了合约规模，延长了交易时间，降低了保证金要求。这些变革近两年来发挥了显著的作用，新华富时A50指数期货的成交量迅猛增长，目前已经达到了日均成交7万手的规模。这些新的变化使得该指数期货重新得到了需要进行套期保值的投资者以及金融机构的青睐。

文章主要通过套期保值理论对沪深300股指期货和新华富时A50指数期货的套期保值效率进行研究，分析目前阶段两者间套期保值的效率哪个更好，并尝试解释造成这种结果的原因，为沪深300股指期货交易规则的完善提出合理的建议。

二、文献综述

研究套期保值的效率落脚点在于研究套期保值中的最关键因素，即期货相对于现货的最优套期保值比。而最优套期保值比理论最早具有代表性的提出者是Johnson(1960)&Stein(1961)，这两位学者都是以Markowitz的均值方差框架为分析基础。他们认为交易者进行套期保值实际上是对现货和期货的资产进行组合投资，套期保值者需要对投资组合的方差即投资风险进行量化，在使其投资组合方差最小化来确定现货和期货间进行套期保值的最优套期保值比率以使其投资风险最小。而最优套期保值比的估计方法主要分为静态估计和动态估计两类。

在静态估计方法中通常假定最优套期保值比率为常数不随时间变化。Ederington(1979)将OLS方法应用到了金融期货市场并提出了度量套期保值有效性的方法及具体的度量指标。但在OLS方法中存在大量与实际情况不相符的假设，例如期现货的价格分布不随时间变化，序列无自相关性、无异方差及协整关系的存在等，在许多研究中也都得到了证实。Bell&krasker (1986)的研究发现用OLS方法得到的最优套期保值比率是有偏的。Herbst(1989)&Myers(1989)等的研究发现从OLS回归方程中得到的最优套期保值比率会受到残差序列的自相关性影响。为此他们利用双变量向量自回归模型(Bivariate Vector Autoregression，BVAR)来增加模型的信息量解决估计方程残差序列的自相关问题。但是VAR模型并不完美，同样也存在缺陷。在VAR模型中并没有考虑现货价格和期货价格中间存在的协整关系对最优套期保值比的影响，这种影响也会导致由模型得到的最优套期保值比有偏，进而导致套期保值比率过低，影响最终套期保值操作的风险控制效果。Lien(1993)&Sim(2001)[1]等的研究表明利用误差修正模型(Error Correction Model，ECM)，Ghosh(1993)[2]等的研究发现利用向量误差修正模型(Vector Error Correction Model，VECM)都可以很好地解决上述问题。同样，误差修正模型也存在问题，主要表现在不能处理平稳的时间序列数据，另外由该方法得到的最优套期保值比率仍然是静态的，不能随时间发生变化。而现实中现货和期货间的联动关系是随着市场环境的改变而不断变化的，静态最优套期保值比无法满足长期、动态条件下套期保值的需要。

由于金融时间序列存在条件异方差，即具有时变的二阶矩，因此最先由Bollerslev在Engle提出的自回归条件异方差(ARCH)基础上提出的广义自回归条件异方差模型，(GRACH)的引入为研究动态最优套期保值比奠定了基础。随后Bollerslev等(1988)提出的多元GARCH模型，以及后来出现的CCC-GARCH (Constant Conditional Correlation GARCH)模型、BEKK-GARCH (Baba Engle Kraft Kroner，GARCH)模型都较好地解决了条件异方差和时变的问题。此后被Park(1995)[3]&Chou等(1997)[4]众多学者应用于期货最优套期保值比率的计算中。另外，同时考虑套期保值比率的时变性以及期现货价格之间的协整关系对套期保值比率的影响，Kroner&Sultan(1993)[5]将ECM与GARCH类模型结合在一起提出了ECM-BGARCH模型。

国外学者对最优套期保值比的研究大体上多认为动态模型优于静态模型，如Allen(2005)[6]&Lee(2009)[7]等。也有部分学者，如Thomas&Brooks(2001)[8]的研究表明利用动态模型得到的最优套期保值比并没有明显优于静态模型。国内学者对期现货间最优套期保值比率的研究也有很多，就股指期货而言，研究的对象与方法随着时间和市场的变化而不断演变。早期由于国内没有股指期货推出，研究多是利用国外股指期货数据，如徐国祥和檀向球(2004)[9]利用香港股市和恒生指数期货作为期现货组合，对最优套期保值率进行了实证研究，发现系统性风险越高的样本股，套期保值的效果越好。之后随着国内股指期货仿真交易系统的推出，高辉和赵进文(2007)[10]利用OLS模型、双变量自回归模型和误差修正模型等方法，对沪深300股指和沪深300股指期货仿真数据进行了最优套期保值比的实证研究。王晓琴(2007)等选出20只沪深300指数样本股，使用沪深300股指期货仿真数据进行了最优套期保值比的实证研究。梁斌等(2009)[11]运用多种静态和动态模型，通过沪深300股指期货仿真数据研究最优套期保值比，发现动态套期保值模型优于静态套期保值模型。在沪深300股指期货正式推出后，佟孟华(2011)[12]采用OLS、ECM-BGARCH等模型对沪深300指数和沪深300股指期货进行了套期保值比的实证研究，结果也表明动态模型的套期保值比要优于静态模型。

但现有研究对于在国内A股市场中运用股指期货进行套期保值的研究并不全面，因为目前的研究只涉及沪深300股指期货与A股现货间的套期保值，但当前可以用来对国内A股进行套期保值的期货工具除了沪深300股指期货以外还有在新加坡交易所已经上市多年的新华富时A50指数期货。而国内对于该工具套期保值效率的研究还是空白。由于该指数期货相对于限制较多的沪深300股指期货的诸多优点，已成为许多以QFII为代表的海外机构进行A股现货套期保值对冲风险的首选工具。新华富时A50指数期货套期保值的效果究竟如何？与沪深300指数期货相比，哪个效果更好？文章运行沪深300股指期货和新华富时A50指数期货的真实交易数据，并利用2012年3季度基金十大重仓股构建现货投资组合，通过套期保值比的静态和动态模型的实证研究来比较沪深300股指期货与新华富时A50指数期货间的套期保值效率并试图回答上述的问题。

三、研究方法与模型

1.最优套期保值比的确定

最早提出利用Markowitz的投资组合理论来解释套期保值的是Johnson(1960)等。在投资组合理论中，套期保值的交易者实际上是对现货和期货的资产进行组合投资，期货市场和现货市场交易头寸的配比取决于套期保值者对投资组合的预期收益率和方差，最优的交易头寸配比应该能使得收益风险最小化或者投资组合的效用函数最大化。

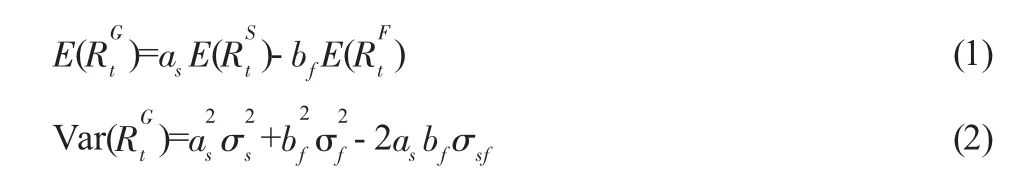
为使投资组合的风险最小化，可对(2)式的右端关于bf求一阶偏导数，由以下条件，可求得时点t投资组合风险最小化的套期保值比率h*为：

除了动态模型的时变方差与协方差以外，公式(3)的结果与由普通的OLS模型得到的套期保值比类似。因为当新息开始影响市场时，条件方差与协方差会改变并促使最优套期保值比发生改变。

2.套期保值理论模型

（1）OLS模型。假设一定阶段内，投资组合现货的收益率与期货的收益率呈线性关系，那么通过建立二者间的线性关系就可以估计最优套期保值比，具体如下式所示：

（2）向量误差修正模型(VECM)。由于金融时间序列大多是非平稳的，且在投资组合与股指期货的价格序列之间通常存在长期的协整关系，另外短期两者之间也存在动态的相互影响关系，向量误差修正模型恰好可以满足上述条件，投资组合与股指期货的VECM模型具体如下式所示：

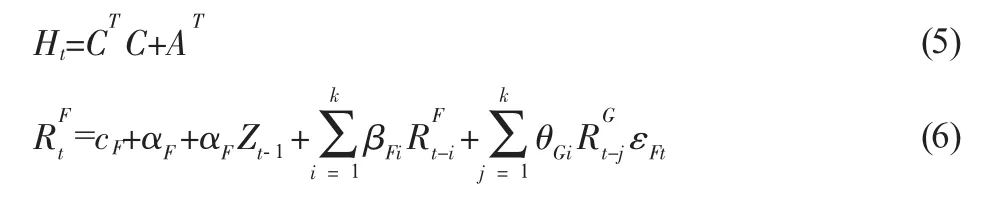
其中，Zt-1=lnGt-1-(a+blnFt-1)为代表投资组合与期货对数价格序列间长期协整关系的误差修正项，αβθ为常数项，α、β与θ为变量系数，εGt与εFt独立同分布，因此最优套期保值比h*为Cov(εGt，εFt)/Var(εFt)。VECM模型的不足之处在于，由它得到的套期保值比依然是静态的，无法反映时变的新息对最优套保比值的影响。

（3）ECM-BGRACH模型。OLS和VECM模型得到的都是静态最优套期保值比，为了考量市场时变的新息对套期保值效率的影响，GARCH类能反映时变新息影响的动态模型越来越多地被应用。为了既考量现货价格与期货价格间的协整关系，又考量残差项的时变异方差性。Kroner(1993)等提出了ECM-BGARCH模型。Lien等(2006)也提出了类似的模型，并指出基差效应对套期保值效果存在重要影响。基差在ECM模型中体现为期现货价格之间存在的长期协整关系，可以用误差修正项来表示。因此，均值模型如下式所示：

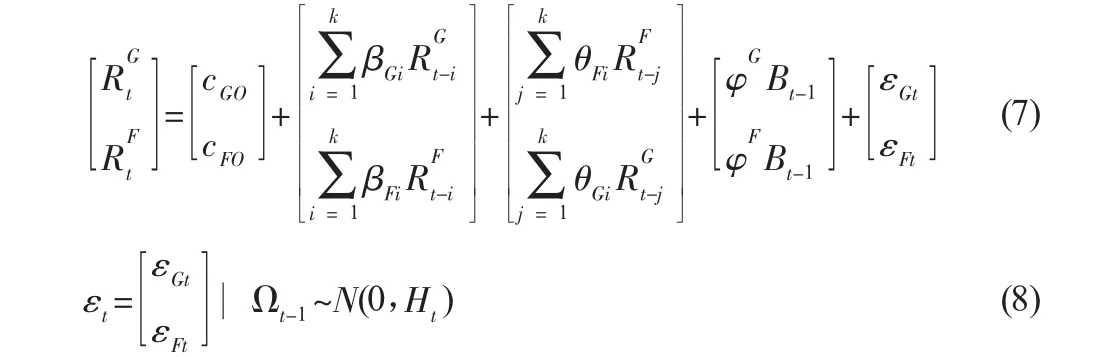
其中Bt-1为反应长期均衡关系的误差修正项，表示为：，它是来自OLS回归方程的误差项。残差项服从GARCH过程，Ωt-1是在时刻t-1的信息。文章选用的条件方差模型为GARCH(1，1)-BEKK模型，模型的具体形式如下式：

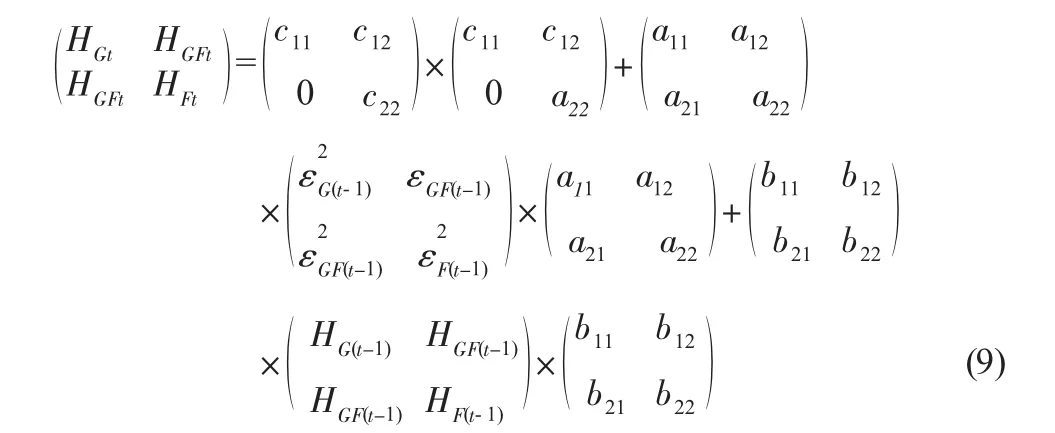
假设在该模型形式中系数矩阵Ai和Bj为对角矩阵，则条件方差协方差方程简化为：

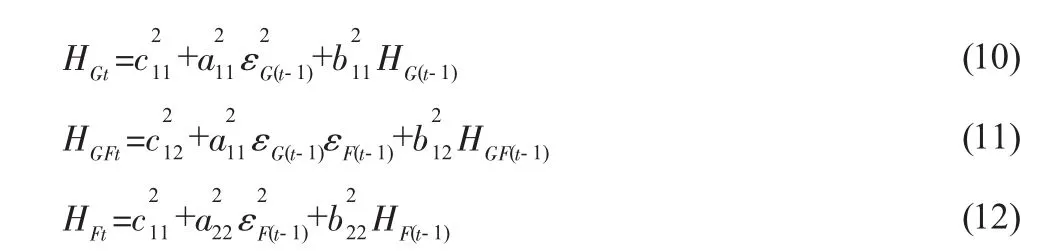
GARCH(1，1)-BEKK模型的优点在于矩阵Ht满足了的正定性且与普通形式相比模型具有较少参数。利用该模型估计时变套期保值比h*，需要首先估计条件方差协方差方程的参数，之后通过估计式预测每个时点的条件方差和协方差。在根据预测值，计算时变最优套期保值比率，具体的表达式如下：

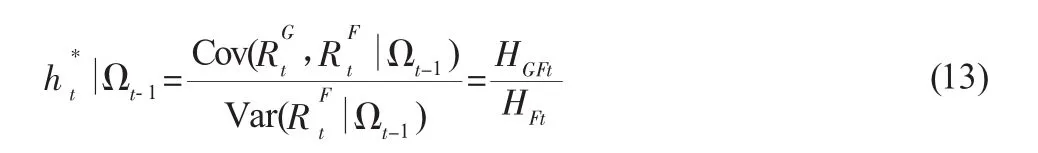
在实证的过程中，为了较好的捕捉序列的非正态性，文章假定条件残差向量服从二元t分布。

3.套期保值绩效的度量

套期保值绩效度度量较常用的是基于风险最小化的传统套期保值绩效指标方法，该方法由Ederington(1973)提出。具体形式如下：

其中，Var(RU)表示为进行套期保值的投资组合收益率方差，Var(RH)表示为进行套期保值后投资组合收益率方差。通过上式可知，套期保值绩效指标HE越大，则套期保值效果越好。

四、实证检验

1.数据说明与变量定义

文章选择2012年第三季度披露的偏股型基金10大重仓股作为构建投资组合的成分股，假设投资组合的规模为5000万元，每只成分股日均投资500万元。并以各成分股的日收盘价格按上述假设构造投资组合的收盘价格，各成分股的具体信息详见表1。选择沪深300股指期货当月连续合约的日收盘价数据，新华富时A50指数期货交易所交易（非电子盘交易）当月连续合约的日收盘价格。数据选择期间为2012年8月1日至2012年11月30日，共83个观测值。数据来源为Wind& Bloomberg金融数据终端。各数据定义变量为，以GPt代表构建的投资组合在第t日的收盘价，FPt代表沪深300股指期货在第t日的收盘价，APt代表新华富时A50指数期货在第t日的收盘价。因此投资组合的日收益率、沪深300股指期货的日收益率和新华富时A50指数期货的日收益率分表表示为：

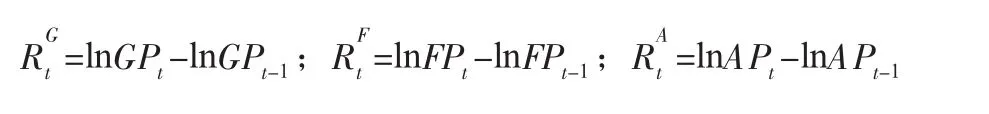
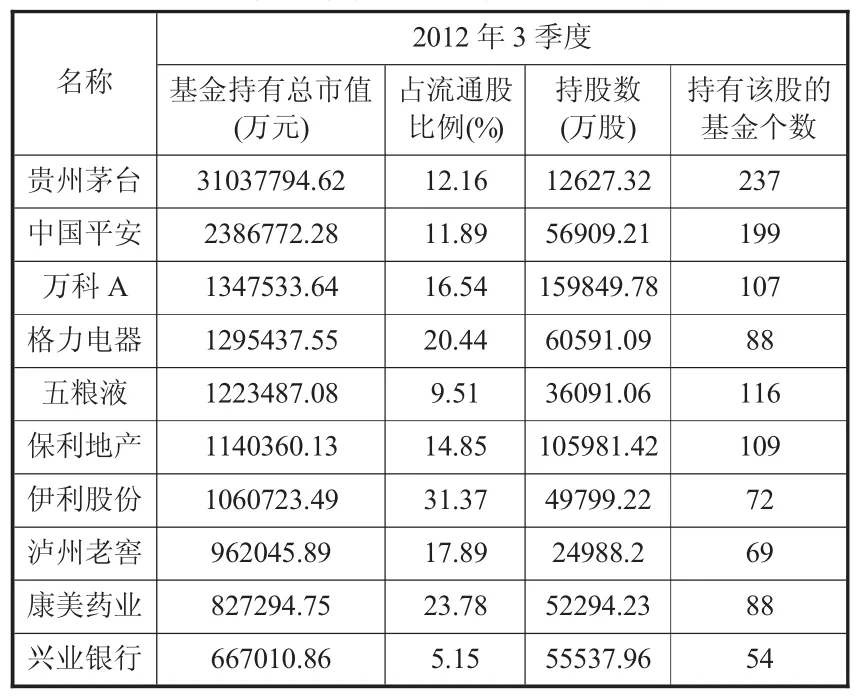
表1 2012年3季度A股市场基金十大重仓股

2.数据的基本统计分析

现货投资组合价格与期货价格序列的走势越趋于一致、相关性越高则套期保值的效果越好。因此首先利用EViews软件分析现货投资组合与沪深300股指期货和新华富时A50指数期货的对数价格序列走势图，如图1所示。

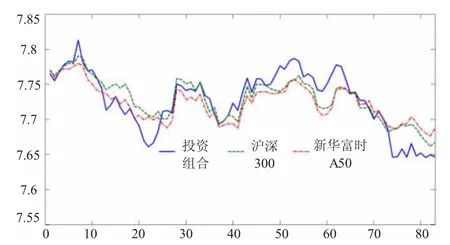
图1 投资组合、沪深300股指期货、新华富时A50指数期货对数价格序列走势图

从图1可以看出，现货投资组合与沪深300股指期货和新华富时A50指数期货的对数价格走势基本趋同，相关程度非常高，符合构建套期保值组合的基本要求。在计算现货投资组合与沪深300股指期货对数价格序列的相关系数和现货投资组合与新华富时A50指数期货对数价格序列的相关系数后，可以知道投资组合与沪深300股指期货和新华富时A50指数期货的相关系数都较高，均超过0.86。且投资组合与新华富时A50指数期货的相关系数要略高于与沪深300股指期货的相关系数。在对投资组合、沪深300股指期货与新华富时A50指数期货收益率序列进行基本统计性分析后可以发现，三个收益率序列的峰度都大于3，偏度均小于0，三个收益率序列均有尖峰、左偏的特征。三个收益率序列的JB统计量均大于20，因此显著拒绝三个收益率序列符合正态分布。三个序列的自相关滞后36期的Q统计量均超过40，这表明这三个数据序列都存在自相关且有显著的条件异方差。

为保证建立数据模型的有效性，需要对数据序列进行平稳性检验，并对由投资组合分别与沪深300股指期货和新华富时A50指数期货组成的数据序列组进行协整检验。文章采用ADF单位根检验，检验数据序列的平稳性，使用Johansen协整检验，检验数据序列组之间是否存在长期的协整关系。检验结果如表2所示。由表2的ADF单位根检验结果可知，投资组合、沪深300股指期货和新华富时A50股指期货的对数价格序列在5%的显著性水平下不能拒绝有一个单位根的原假设，因此均为不平稳的数据序列。而三者经过一阶差分后的收益率序列则在5%的显著性水平下可以拒绝有一个单位根的原假设，均为平稳的数据序列，可以利用Johansen协整检验来分别检验投资组合与沪深300股指期货和新华富时A50指数期货对数价格序列间的协整关系。

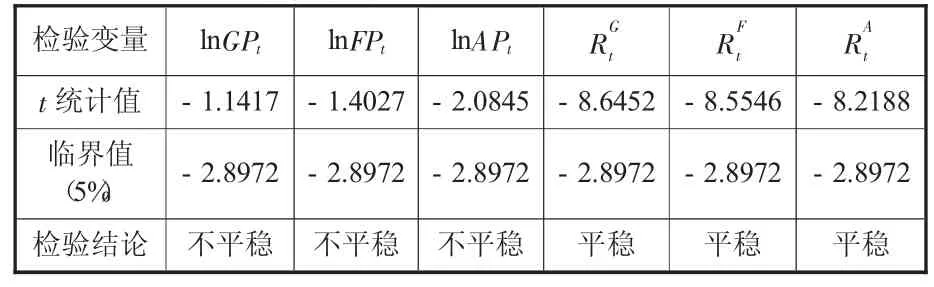
表2 投资组合与两种期货对数价格和收益率序列ADF单位根检验

再对两组对数价格序列组合进行Johansen协整检验，并同时采用特征根和最大特征值方法进行协整检验后，结果如表3所示。由表3可以看出，在5%的显著性水平下，两组组合的特征根迹检验和最大特征跟检验都拒绝了没有协整向量的原假设而没有拒绝至少有一个协整向量的原假设。因此该结果表明在投资组合与沪深300股指期货和新华富时A50指数期货的对数价格序列间存在协整关系。

3.利用模型估计最优套保比

（1）利用OLS估计最优套保比。以投资组合现货的收益率作为被解释变量，分别以沪深300股指期货收益率和新华富时A50指数期货收益率作为解释变量，利用回归方程分别得到两组不同的结果。结果显示两组的解释变量的估计系数均显著，投资组合与沪深300股指期货间的最优套保比为0.8802，而投资组合与新华富时A50指数期货间的最优套保比为0.9093。

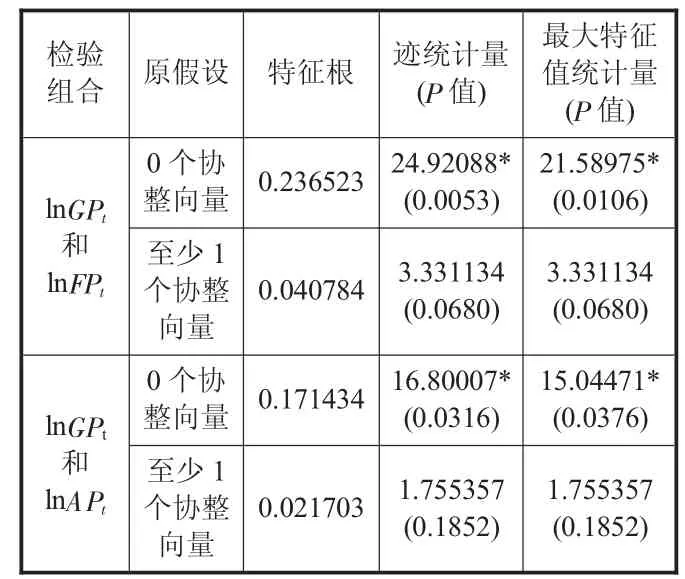
表3 投资组合与两种期货收益率序列JJ协整关系检验

（2）利用向量误差修正模型(VECM)估计最优套期保值比。表3的Johansen协整检验表明投资组合对数价格序列分别与沪深300股指期货价格序列和新华富时A50指数期货价格序列间存在协整关系。因此文章分别对三个对数价格序列的一阶差分和建立向量误差修正模型。根据AIC和SC信息准则，确定由两组分别建立的滞后一期的VECM模型，从估计结果中分别求出残差的相关系数矩阵，表4分别给出了两组模型的估计结果，其中包括第一组模型中的的方差的方差以及两者的协方差和最优套保比，第二组模型中的方差的方差以及两者的协方差和最优套保比

由表4可以看出，两组从两组VECM估计模型计算出的最优套保比分别为0.8953和0.9103，均大于由OLS估计模型计算出的最优套保比。这是由于VECM模型相比OLS模型考虑了变量间滞后项的相互影响和变量间的协整长期均衡关系。且由投资组合与新华富时A50指数期货计算出的最优套保比也略大于由投资组合与沪深300股指期货计算出的最优套保比。

（3）利用ECM-BGARCH(1,1)模型估计最优套保比。由于从投资组合、沪深300股指期货和新华富时A50指数期货的收益率序列存在“尖峰”和左偏的非正态特征，因此文章以VECM(1)构建两组不同组合的均值方程，以BGARCH(1，1)针对两组不同的残差组合构建条件方差方程。通过最大似然估计估计模型参数，并利用估计的结果分别计算两组不同的时变条件方差与时变条件协方差。再利用时变条件方差和时变条件协方差分别计算出两组不同的动态时变最优套保比。时变条件方差方程的估价结果如表5所示。

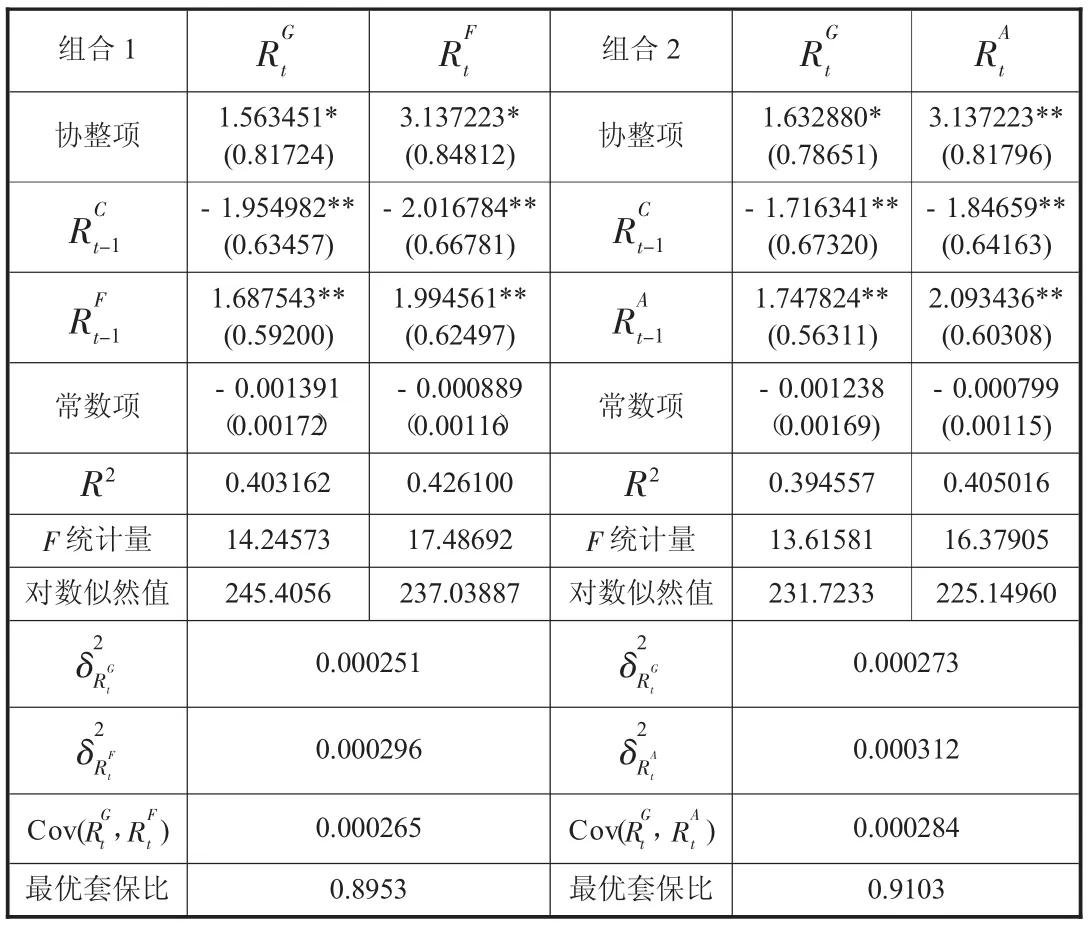
表4 VECM模型估计结果

表5 ECM-BGARCH模型估计结果

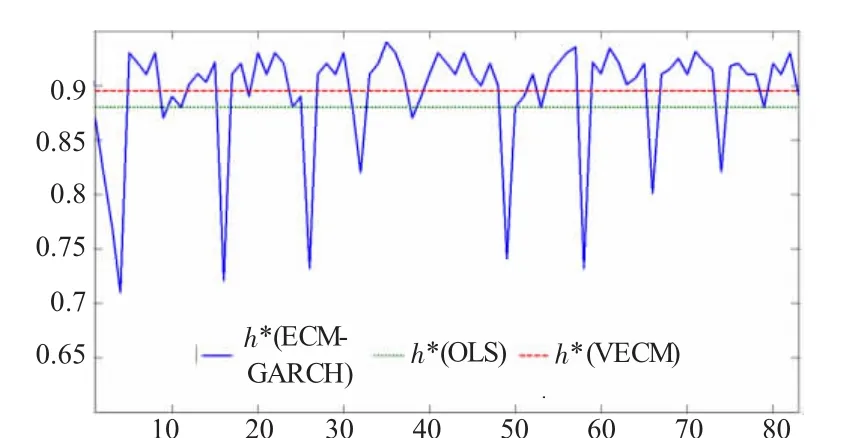
图2 投资组合与沪深300股指期货不同模型最优套保比率比较

图3 投资组合与新华富时A50指数期货不同模型最优套保比率比较

由于时变条件方差和时变条件协方差是动态变化的，因此根据以上估计结果计算得到的最优套期保值比也是动态的变化的，且具有一定的波动性。按照最优套保比计算公式经计算后得到投资组合与沪深300股指期货间的动态最优套保比均值为0.9116。投资组合与新华富时A50指数期货间的动态最优套保比均值为0.9142。

4.不同模型的套期保值比与套期保值绩效比较

利用上述计算结果，针对OLS模型和VECM模型的静态最优套保率和ECM-BGARCH模型的时变动态最优套保率分别对投资组合与沪深300股指期货和投资组合与新华富时A50指数期货建立走势图如图2、3所示。

从图中可看出，在两组数据构成的图中由ECM-BGARCH模型得到的动态最优套期保值比时变序列在大多数时候都大于由OLS和VECM模型得到的静态套期保值比常数序列。因此可以表明静态模型普遍会低估套期保值中投资组合价格所需对应的期货合约数量，而如ECM-BGARCH这样的动态模型在套期保值操作中可以更有效的降低投资组合风险。另外从两组图形的对比中可以看到，无论是OLS和VECM等静态模型还是ECM-BGARCH这样的动态模型，新华富时A50指数期货对应的最优套保比均大于沪深300股指期货对应的最优套保比。

最后，按照“风险最小化”原则和式(14)对投资组合与沪深300股指期货和投资组合与新华富时A50指数期货利用三种不同估计模型计算得到的套期保值绩效指标进行比较分析，结果如表6所示。针对两个组合分别对比三种不同模型的套期保值绩效，投资组合与新华富时A50指数期货的套期保值绩效均略大于投资组合与沪深300股指期货的套期保值绩效。可见，从套期保值绩效上看，新华富时A50指数期货要好于沪深300股指期货。即通过新华富时A50指数期货进行套期保值相比于沪深300股指期货能更有效地规避市场的系统性风险。

五、结论

针对国内A股市场同时存在的两种不同套期保值金融工具沪深300股指期货和新华富时A50指数期货，文章通过基金十大重仓股构建投资组合，并分别与上述两种不同的套期保值工具配对进行套期保值效率的研究，实证检验的结论主要有，从收益率序列的相关程度来看，新华富时A50指数期货与投资组合的相关系数要高于沪深300股指期货。从利用包括OLS和VECM在内的静态套期保值模型的估计结果计算得到的静态最优套期保值比上看，新华富时A50指数期货与投资组合件的最优套保比要高于沪深300股指期货。同样从利用ECM-BGARCH (1，1)这样的具有时变条件方差和协方差的动态套保模型得到的时变最优套保比上看，新华富时A50指数期货也要好于沪深300股指期货。最后，在基于最小风险原则的套期保值绩效指标的比较中，无论是静态模型或是动态模型得到的结果也都显示新华富时A50指数期货要优于沪深300股指期货。因此现阶段新华富时A50指数期货的套期保值效率要优于沪深300股指期货。之所以会有上述结果，可能的原因主要有以下两点：首先，超出沪深300股指期货9个小时，使其可以充分提前反映A股收盘后下午和晚间出现的新息对市场的影响；其次，新华富时A50的合约交易规则中并没有向沪深300股指期货一样限制如公募基金和QFII等金融机构只能利用期指进行套期保值而不能进行套期。这样在有“坏”的新息使市场出现超跌后，新华富时A50指数期货就会立刻有金融机构的大量买盘纠正市场的非理性行为。综上可知，文章建议沪深300股指期货可以进行适当的改革，包括设立适当时间的晚间电子盘交易并允许金融机构在一定份额内进行期指套利交易以提升其市场功能发挥的效率。

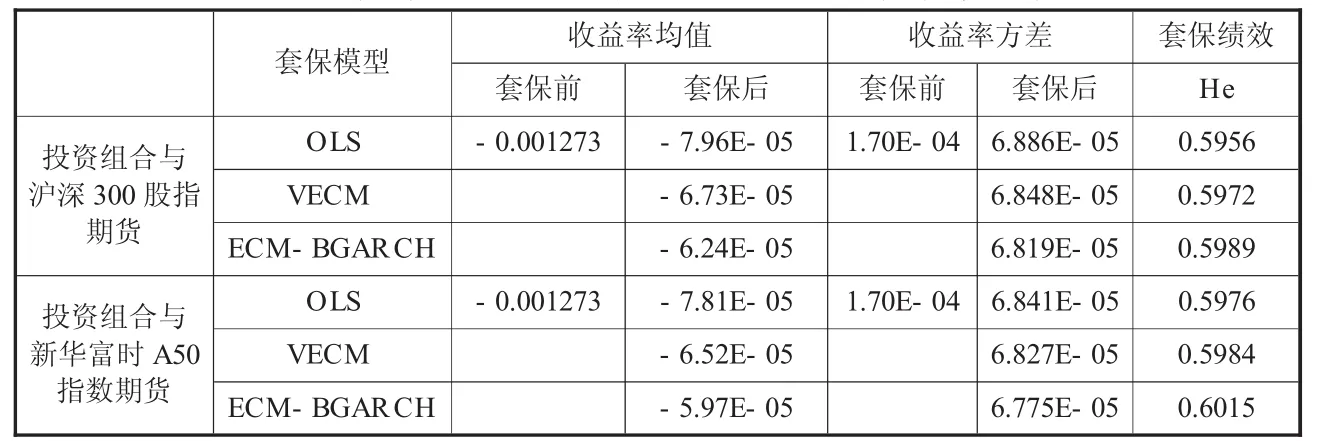
表6 沪深300与新华富时A50套期保值绩效比较

[1]Sim A B，Zurbruegg R.Optimal hedge ratios and alternative hedging strategies in the presence ofcointegrated time-varyingrisks[J].The European Journal ofFinance，2001，7(3):269-283.

[2]Ghosh A.Hedgingwith stock indexfutures:Estimation and forecastingwith errorcorrectionmodel[J].JournalofFuturesMarkets，1993，13(7):743-752.

[3]Chou W L，Denis K K，Lee C F.Hedging with the Nikkei index futures: The convential model versus the error correction model [J].The Quarterly ReviewofEconomics and Finance，1997，36(4):495-505.

[4]Park，T.H，L.NSwitzer.Bivariate GARCH Estimation of the Optimal Hed -ge Ratios for Stock IndexFutures：ANote[J].Journal ofFutures Markets，1995.

[5]Kroner KF，Sultan J.Time-varyingdistributions and dynamic hedgingwith foreign currencyfutures[J].Journal of Financial and Quantitative Analysis，1993，28(4).

[6]Yang W，Allen D E.Multivariate GARCH hedge ratios and hedging effectiveness in Australian futures markets[J].Accounting&Finance，2005，45(2):301-321.

[7]Lee H T.Acopula based regime switchingGARCH model for optimal futures hedging[J].Journal offutures markets，2009，29(10):946-972.

[8]Thomas S，Brooks R.GARCH based hedge ratios for Australian share price index futures:does asymmetry matter[J].Accounting，Accountability and Performance，2001，7(1):61-76.

[9]徐国祥，檀向球.指数期货套期保值实证研究—以香港恒生指数期货为例 [J].统计研究，2004(4):49-52.

[10]高辉，赵进文.沪深300股指套期保值及投资组合实证研究 [J].管理科学，2007，20(2):80-90.

[11]梁斌，陈敏，缪柏其，吴武清.我国股指期货的套期保值比率研究 [J].数理统计与管理，2009(1):143-151.

[12]佟孟华.沪深300股指期货动态套期保值比率模型估计及比较—基于修正的ECM-BGARCH(1，1)模型的实证研究 [J].数量经济技术经济研究，2011(04).

（责任编辑：HLT）

The Comparative Study of Stock Index Future Hedging Efficiency——Based on CSI 300 Stock Index Futures and FTES Xinhua A50 Index Futures

FAN Tai-qi，HAN Fu-ling
（School of Management and Economics，Beijing Institute of Technology，Beijing 100081，China）

Through constructing portfolio with the ten great overweight held stocks by funds，the paper makes comparative research for the CSI 300 stock index futures and the FTES Xinhua A50 index futures by using daily data of them to find the hedging efficiency difference between them and the reasons that cause the difference.Based on OLS，VECM and ECM-GRACH static and dynamic hedging model and the minimum risk hedging performance indicators，the author finds that the FTES Xinhua A50 index futures are better than the CSI 300 index futures in the static optimal hedge ratio，time-varying optimal hedge ratio and hedging performance indicators.According to the results，it can be found that the difference results from the different contract and trading rules between the two financial instruments The author suggests that building up the evening electronic trading market in appropriate time and allow financial institutions to arbitrage by using stipulated quota for enhancing hedging efficiency of market function of CSI 300 stock index futures.

Stock index futures；Hedging；Financial instruments；Financial investment

F724.5

A

1004-292X（2014）10-0096-06

2014-05-29

范泰奇（1980-），男，江西瑞昌人，博士研究生，研究方向：金融机构与金融市场；韩复龄（1964-），男，河北正定人，教授，博士生导师，主要从事金融机构与金融市场研究。