基于担保方信用风险的可转债定价问题研究

傅 毅,张寄洲,仇亚尊

(1.上海师范大学 商学院, 上海 200234; 2.上海师范大学 数理学院, 上海 200234)

0 引 言

随着债券市场的发展,债券市场上出现了多种债券衍生产品,如可转换债券等.可转换债券是20世纪7,80年代兴起的一种混合金融产品,目前,已成为中国证券市场研究的热点之一.可转换债券是指持有者可以在一定时期内按一定比例或价格转换成一定数量的另一种证券的债券,通常转换为发行公司的普通股票,一般具有较低的票面利率.从本质上讲是在发行公司债券的基础上,附加了一份期权,并允许购买人在规定的时间范围内将其购买的债券转换成指定公司的股票.可转债具有债权和期权的双重特征,并具有如下性质: (1) 债权性: 与其他债券一样,可转债也有利率和期限,投资者持有到期可以收取本息.(2) 股权性: 可转债转换成股票后,原债券持有人变为公司的股东,可参与公司的经营与红利分配.(3) 可转换性: 债券持有人可以按约定的条件将债券转换成公司股票,如果债券持有人不想转换,则可以继续持有直到期满收取本息,或者在流通市场出售变现.如果持有人看好发债公司股票的增值潜力,则可按约定的条件转换成股票,发债公司不得拒绝.

近年来,许多学者主要从以下几个方面研究了可转债的定价等相关问题.

随着Black-Scholes-Merton期权定价的模型的建立,一些学者在期权定价模型的基础上对可转债进行定价.Ingersoll(1977)[1]、Brennan和Schwartz(1977)[2]最早对可转债的定价问题进行了理论研究,他们通过对公司的市值所满足的随机过程来研究可转债的定价.不同于前面两篇文章,Brennan和Schwartz(1980)[3]将利率的波动性考虑进了可转债的定价中,并利用数值计算得出了可转债的定价.Barone(2003)[4]等人又在以上模型的基础上建立了关于标的资产和利率的双因素模型.Toshikazu(2006)[5]等从另一个角度对可转债进行了定价,将可转债分解成两部分,一部分是纯债券价值,另一部分是转换的期权价值,把未来的债券利息和本金的现值以及认股权证的现值相加得到可转债的理论价值,并用Monte Carlo方法给出了带有重置条款的可转债的定价.

由于发行公司存在信用风险,所以把信用风险考虑进债券的定价中更贴近于现实.目前,研究信用风险主要有两种方法：结构化方法和约化方法.结构化方法是把债券看成关于公司资产的看跌期权,但通常公司的资产情况并不能准确得到.而约化方法则是把公司的破产事件看成是一个外在的泊松过程,用第一次发生跳的时间作为公司的破产时间,其中泊松过程的强度可以从市场相关的数据推得.Kostas(1998)[6]等对带有信用风险的可转债进行了定价.Ayache(2003)[7]等利用对冲的思想通过构造投资组合对带有信用风险的可转债进行了定价.Wang(2010)[8]等人对带有信用风险的永久可转债进行了定价.

为了吸引投资者,发行公司在发行可转债时往往设计一些附加条款.Kyoko(2010)[9]等分析了带有可赎回和可回售条款的可转债的定价,探索了赎回和回售的实施边界,并研究了可赎回和回售条款对可转债的价值和最优策略的影响,Fahuai(2011)[10]等对可转债定价的自由边界问题进行了研究,证明了变分不等式的解的存在性和唯一性,并且得到了自由边界的单调性、有界性和光滑性等性质.Toshikazu(2006)[5]等研究了带有重置条款的可转债定价.熊思灿(2010)[11]等给出了附有巴黎期权特性的重置条款的可转债定价模型,并采用有限差分方法求解模型.

另外,由于发行债券的公司都存在潜在的违约风险,而公司的信用等级对可转债的价格有着重要的影响,所以发行公司往往通过信用增级的方式来提高可转债的价格,其中信用增级方式中第三方担保得到了广泛的应用.任学敏(2009)[12]等用约化方法对有第三方担保的企业债券进行了定价,得到了在担保的情形下企业债券满足的微分方程.刘易(2013)[13]等人在结构化模型的框架下,考虑了担保公司和被担保公司之间的相关性,得到了具有相关性的第三方担保的公司债券所满足的偏微分方程.

如上所述,考虑带有担保的可转债的定价问题具有重要的现实意义.本文作者在约化模型的框架下对可转债进行了定价,并考虑了可转债的担保方可能违约的情况,运用偏微分方程的方法得到了有担保的可转债的定价公式.文章的第一部分对模型做了一些假设，第二部分利用对冲技巧分别就担保公司是否违约两种情况建立了可转债的数学定价模型，并在文章的第三部分对模型求解,最终得到可转债的显式解，第四部分对模型的参数进行了分析.

1 基本假设

假设1A公司发行了零息票可转换债券,到期日为T,公司B为其作担保.

假设2若发行公司A破产,其可转债投资人的损失将由担保公司B承担.但如果担保公司先于发行公司破产,则担保失效.

假设3发行公司和担保公司的破产是由不可预料事件引发的,违约强度分别为λ1,λ2,违约时间分别记为τ1,τ2.

假设4用Poisson过程的第一次跳来刻画违约,Poisson过程在时间段[s,t]发生k次跳的概率为:

设τ为第一次跳的时刻,则公司在[0,T]时间段内的违约概率为:

P(τ≤T)=1-P(τ>T)=1-e-λT.

假设5发行公司与担保公司违约发生是相互独立的.

假设6发行公司的股票价格S(t)服从几何布朗运动:

dS(t)=μS(t)dt+σS(t)dW(t) .

其中μ为期望回报率;σ为波动率,且都为常数;W(t)为标准的布朗运动.

假设7发行公司违约后,其股价变化满足:

S+=S-(1-η) .

其中η为常数,表示发行公司违约后,其股价下降的幅度,这里的违约表示广义的违约,即发行可转债的公司可能由于流动性等原因造成不能按时支付息票所导致的违约.

假设8不考虑可转债的可赎回和可回售条款.

假设9假设持有人的转换权只发生在到期日或违约日,转换权行使时一份可转债可转换为k份股票.可转债的连续票息率为q.

2 模型建立

利用Δ-对冲技巧,建立可转债定价的数学模型.首先,构造投资组合：

Πt=Vt-ΔSt,

其中V是发行公司的可转债的价值;S是发行公司的股票价格.

在没有违约的情况下,在[t,t+dt]时间段内,投资组合的变化为：

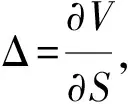
为了对[t,t+dt]时间段内的可转债有无担保进行刻画,将可能发生的情况分为以下两类:

情况一:有担保时可转债的定价模型

考虑违约的情况下,在[t,t+dt]时间段内,发行公司发生违约的概率为λ1dt.假设违约后,发行公司的股价满足假设7.若发行公司先于担保公司违约,则可转债持有人有两种选择:

(1) 按可转债面值F回收,回收率为R(0≤R≤1),其余部分由担保公司承担,债券持有人共获得RF+(1-R)F即F.

(2) 执行转换权,转股得到的股票价值为kS(1-η1).

其中,η1为发行公司违约后,其股价下降的幅度.

这时投资组合Π的价值变化为:

(1)

由无套利原理得:

dΠ=rΠdt.

(2)

整理得:

这样得到了有担保情况下可转债满足的偏微分方程:

(3)

情况二:担保失效时可转债的定价模型

在[t,t+dt]时间段内,发行公司发生违约的概率为λ1dt.担保公司发生违约的概率为λ2dt.若担保公司先于发行公司违约,则发行公司违约后,可转债持有人有两种选择权:

(1) 可转债按面值回收,面值为F,回收率为R,持有人此时得到RF.

(2) 执行转换权,转股后得到的股票价值为kS(1-η2)(η2>η1).

其中,η2为发行公司违约后,其股价下降的幅度.

这时投资组合Π的价值变化为:

由无套利原理得:

这样得到了担保失效情况下可转债满足的偏微分方程:

(4)

以上两种情况分析并得出了可转债分别在有无担保时满足的定价方程,本研究中的定价思路是对每个可能的担保公司的违约时刻τ2,确定相应的发行公司的可转债的价格.

(1) 若0<τ2≤T,显然当τ1∈[τ2,T]时,发行公司失去了担保,其可转债的定价方程为(4).当τ1∈[0,τ2]时,由于担保公司未破产,则发行公司的可转债扔有担保,此时其定价方程为(3).

(2) 若τ2>T时,则在时间段[0,T]内担保公司不破产,发行公司的可转债有担保,此时的定价方程为式(3).

下面计算各种情况的概率:

① 若0<τ2≤T且τ1∈[0,τ2],此时可转债有担保,则其发生的概率为:

(5)

② 若0<τ2≤T且τ1∈[τ2,T],此时可转债无担保,则其发生的概率为:

(6)

③ 若τ2>T,此时可转债有担保,其发生的概率为:

P3=P(τ2>T)=e-λ2T.

(7)

3 模型的求解

在这一节中,将分别求解出偏微分方程(3)和(4).首先,解方程(3).

作变换x=lnS,τ=T-t,定解问题(3)转化为常系数抛物型的Cauchy问题:

作函数变换:V=Ueατ+βx,通过选取适当的α,β,使上式转化为非齐次热传导方程:

(8)

其中

为求解式(8)首先求解以下齐次热传导方程的柯西问题:

(9)

柯西问题(9)的解为:

(10)

然后,再求非齐次热传导方程具有齐次初始条件的柯西问题:

(11)

得到柯西问题(11)的解为:

(12)

最后由叠加原理,由(10)及(12)就得到柯西问题(8)的解为:

整理得:

其中,

(13)

变换回到原变量V(S,t),得到有担保的情形下可转债的价值V1(S,t)为:

其中,

(14)

同理可解方程(4):

其中,d1,d2同上式(13)

变换回到原变量V(S,t),得到无担保的情形下可转债的价值V2(S,t):

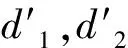
最后得到了可转债的价值V(S,t)为:

V(S,t)=(P1+P3)V1(S,t)+P2V2(S,t).

4 数值分析

本文的前一部分中,作者运用偏微分方程的方法得到了考虑担保方信用风险的可转债的显式解,接下来分析模型中一些参数对可转债价值的影响.

图1为不同时刻与股价所对应的可转债的价值。

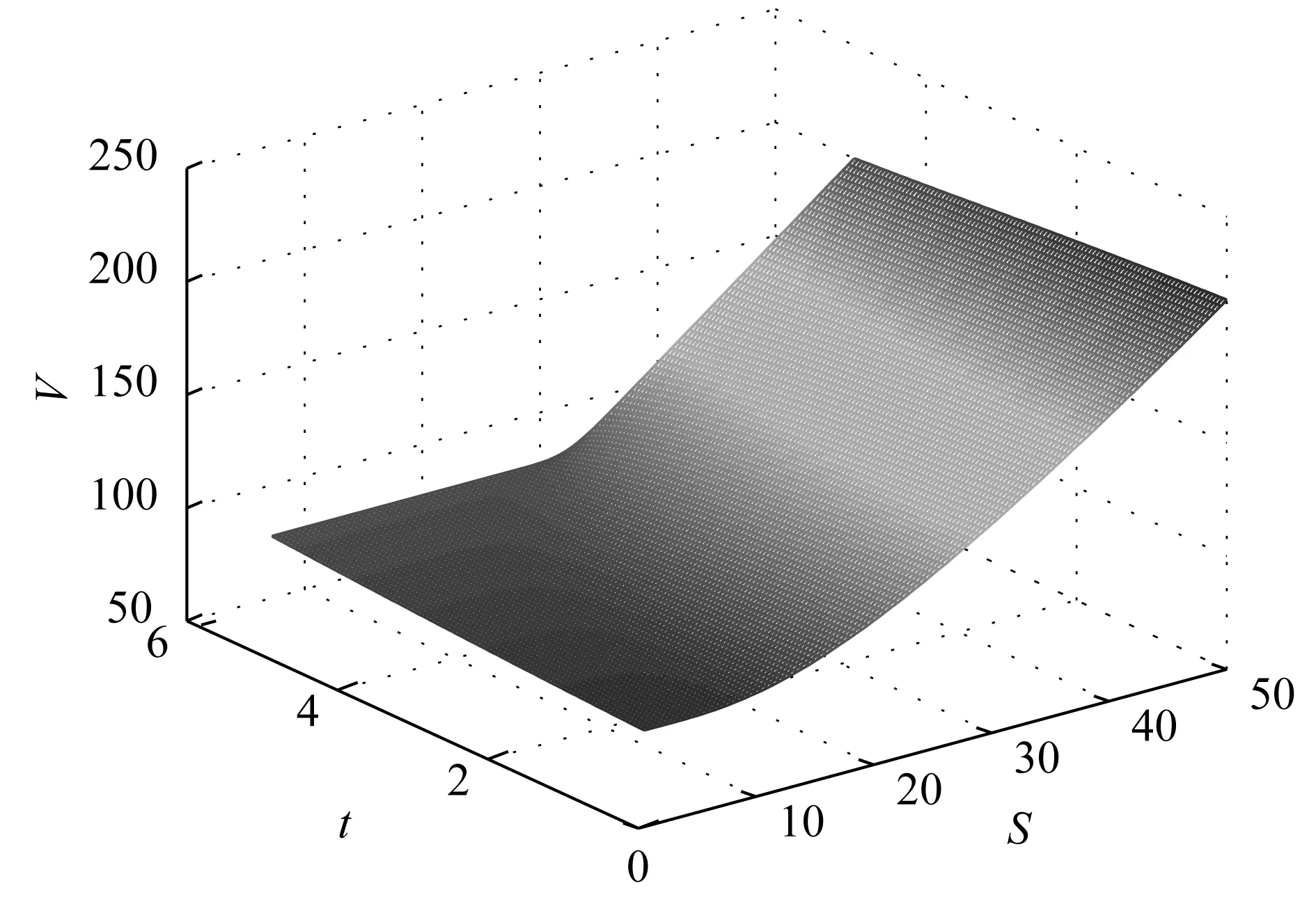
图1 可转债的价值V与时间t股票价格S的关系图

图2为发行公司的违约强度λ1对可转债价值的影响.由图2可看出,随着发行公司的违约强度λ1的增大可转债的价值变小.这是因为当发行公司的违约强度变大时,公司的破产概率变大,从而增加了可转债持有者的可能损失,所以随着发行公司的违约强度λ1的增大可转债的价值变小.

图3和图4为担保公司的违约强度λ2对可转债价值的影响.由图3可以看出当发行公司的违约强度λ1=0.05时,担保公司的违约强度λ2越大可转债的价值越小,成反向关系.同时也可以看出担保公司的违约强度λ2的变化对可转债的价值影响较小.这是因为在发行公司违约概率较小的情况下,担保公司的违约强度的变化对可转债的影响较小.而由图4可以看出当发行公司的违约强度λ1=0.3时,担保公司的违约强度λ2越大可转债的价值越小,成反向关系,且担保公司的违约强度λ2的变化对可转债的价值影响较大,即当发行公司的违约强度较大时担保公司对可转债的价值起的作用会变大.

图5为无风险利率r对可转债价值的影响.由图5可以看出,随着无风险利率r的增大可转债的价值变小.当股票价格远高于转股价格时,可转换公司债券受市场利率影响较小,若价格较低时,可转换公司债券对市场利率变动非常敏感,且成反向关系.

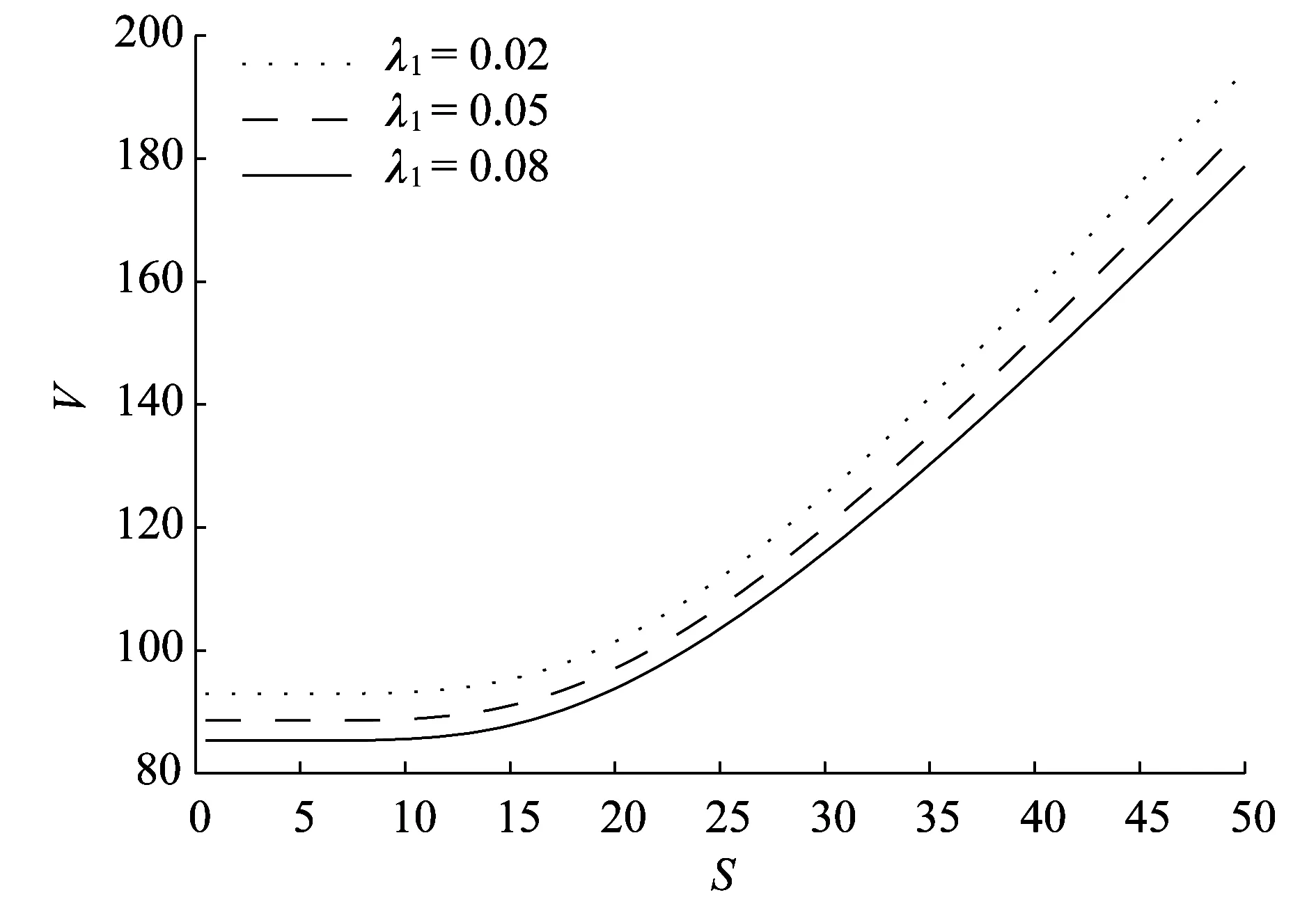
图2 发行公司的违约强度λ1对可转债价值的影响

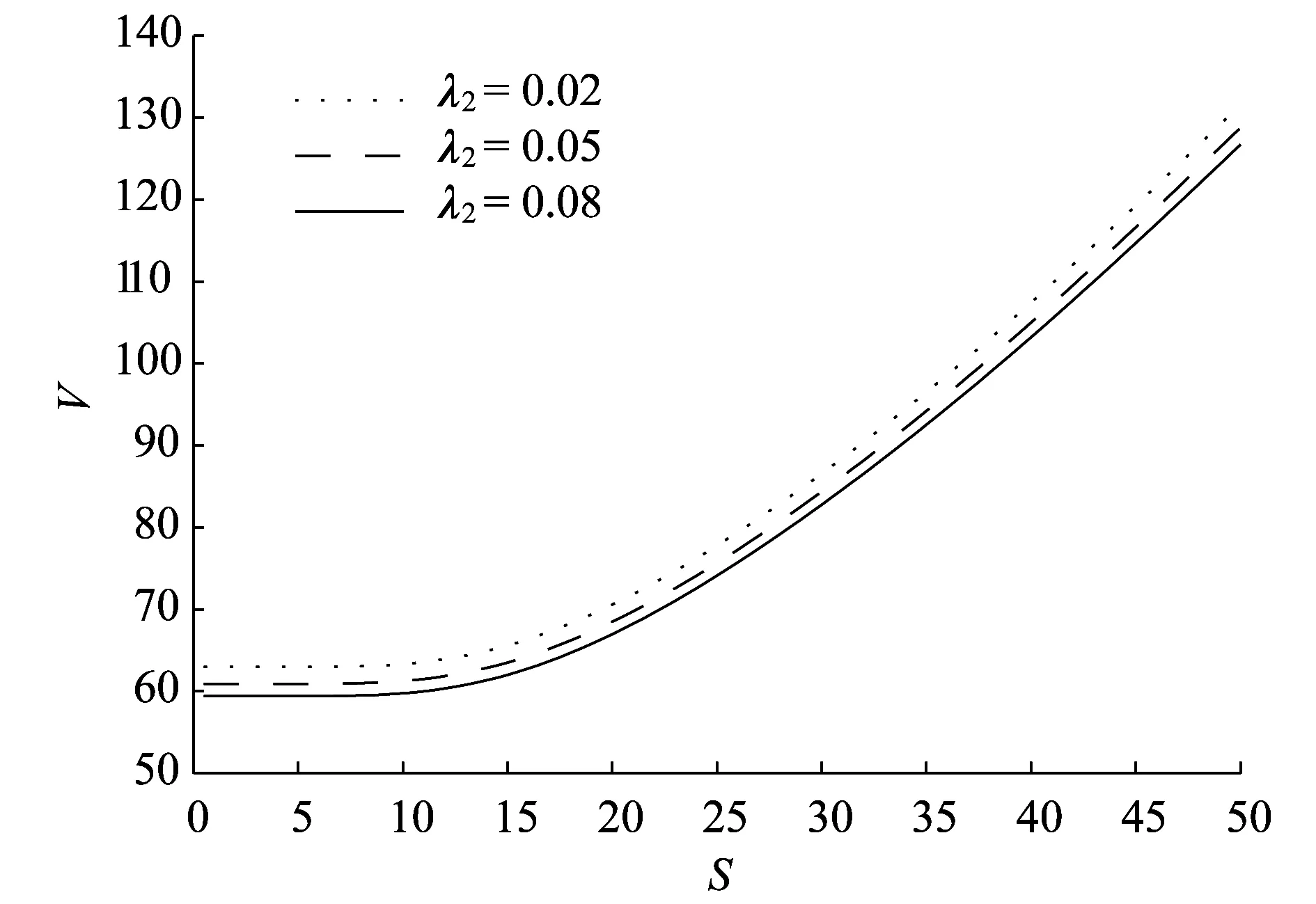
图4 λ1=0.3时担保公司的违约强度λ2对可转债价值的影响

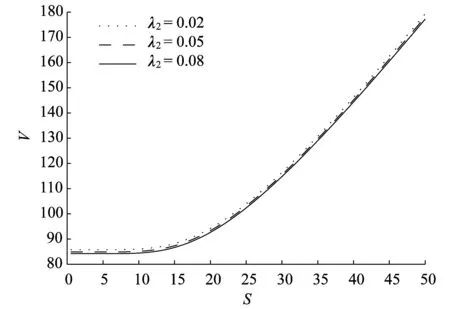
图3 λ1=0.05时担保公司的违约强度λ2对可转债价值的影响

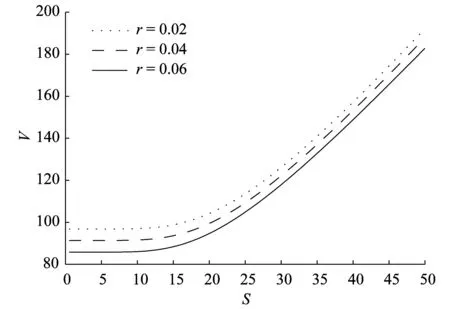
图5 无风险利率r对可转债价值的影响

图6为股票的波动率σ对可转债价值的影响.由图6可以看出,随着波动率σ的增大可转债的价值变大.这是因为股票的波动率越大,可转债的投资者获得收益的可能性就越大,所以可转债的价值就越大.

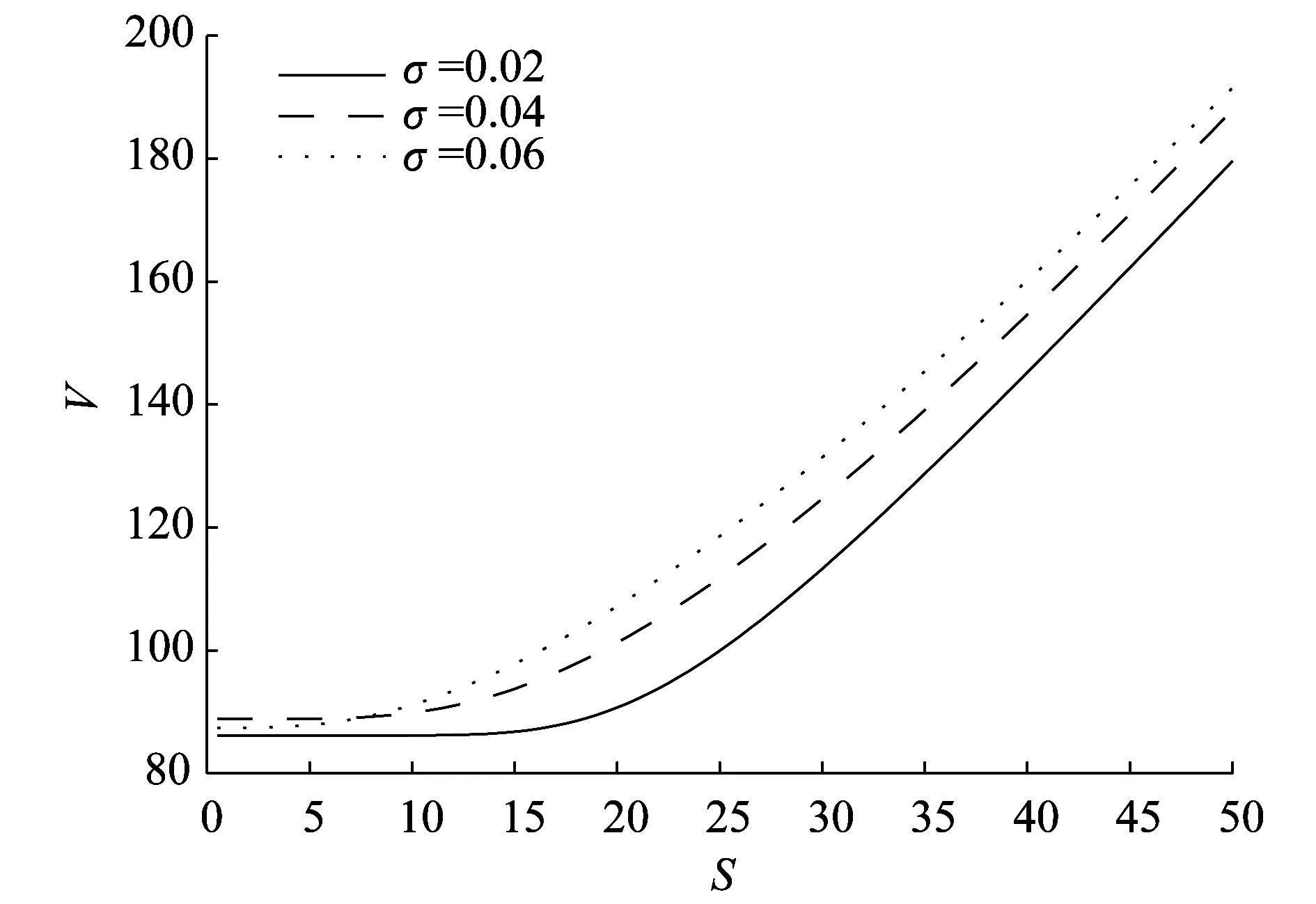
图6 波动率σ对可转债价值的影响

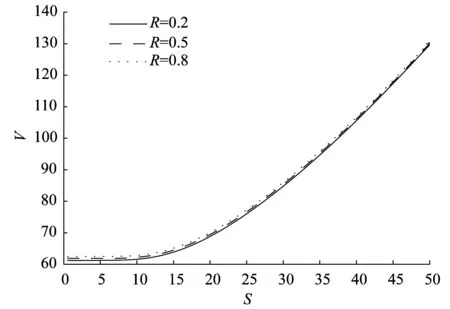
图7 发行公司破产后不同的回收率R对可转债价值的影响

图7为发行公司破产后不同的回收率R对可转债价值的影响.由图7可以看出发行公司破产后的回收率越高可转债的价值越大.同时也可以看出发行公司破产后的回收率对可转债的价值影响是比较小的.这是因为在发行公司违约概率较小的情况下,回收率的变化对可转债的影响较小.

图8为可转债不同的票面利率q对可转债价值的影响.由图8可以看出在其他条件相同的条件下,票面利率与可转债价值成正向关系,可转债的票面利率越高可转债的价值越大,反之亦然.

图9为可转债不同的转股率k对可转债价值的影响.由图9可以看出在其他条件相同的条件下,转股率越高,转股价越低,股票买权执行价格就越低股票买权的价值就越高,可转债的价值就越高.

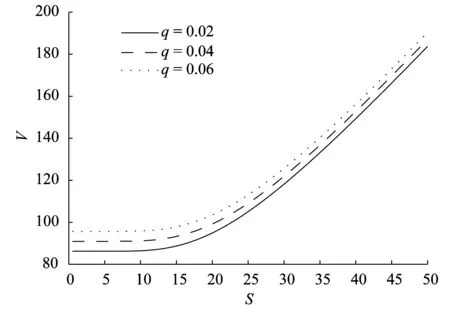
图8 票面利率q对可转债价值的影响

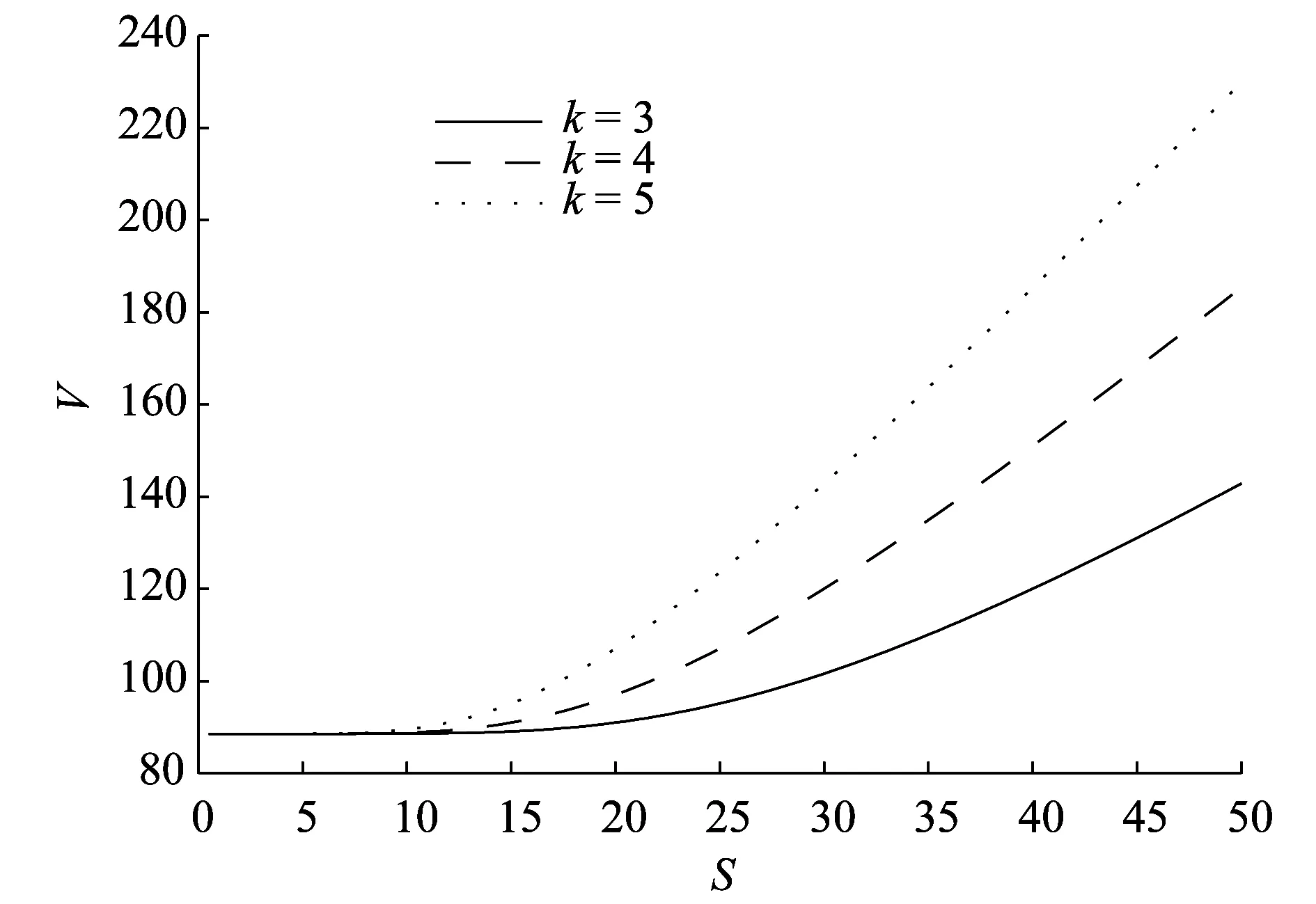
图9 转股率k对可转债价值的影响

5 结 论

本研究是在AFV模型的基础上进行了改进,研究分析了有担保的可转债的定价,并考虑了担保公司是否违约,针对不同情形建立了相应的数学模型,最终得到了担保公司可能违约的情况下可转债的定价公式的显式解,并分析了担保公司在破产和不破产两种不同情形下对发行公司的可转债价格的影响.

参考文献:

[1] INGERSOLL JR J.A contingent-claims valuation of convertible securities[J].Journal of Financal Economics,1977，4:289-322.

[2] BRENNAN M J,SCHWARTZ E S.Convertible bonds:Valuation and optimal strategies for call and conversion[J].Journal of Finance,1977，32：1699-1715.

[3] BRENNAN M J,SCHWART E S.Analyzing convertible bonds[J].Journal of Finance and Quantitative Analysis,1980，15:907-929.

[4] BARONE ADESI G,BERMUDEZ A,HATGIOANNIDES J.Two factor convertible bonds valuation using the method of characteristics finite elements[J].Journal of Economic Dynamics and Control,2003，27:1801-1831.

[5] KIMURA T,SHINOHARA T.Monte carlo analysis of convertible bonds with reset clauses[J].European Journal of Operational Research,2006，168:301-310.

[6] TSIVERIOTIS K,FERNANDES C.Valuing convertible bonds with credit risk[J].Journal of Fixed Income,1998，8:95-102.

[7] AYACHE E,FORSYTH P A,VETZAL K R.The valuation of convertible bonds with credit risk[J].The Journal of Derivatives,2003，11:9-30.

[8] WANG L L,BIAN B J.Pricing of perpetual convertible bonds with credit risk under framework of reduce form[J].Journal of Tongji University,2010，6:935-940.

[9] KYOKO Y,KATSUSHIGE S.The valuation of callable-puttable reverse convertible bonds[J].Asia-Pacific Journal of Operational Research,2010，27:189-209.

[10] ZHOU Y,YI F H.A free boundary problem arising from pricing convertible bond[J].Applicable Analysis,2010，3:307-323.

[11] 熊思灿,钱永江,杨善朝.带重置条款的可转债定价模型及其实证研究[J].数学的实践与认识,2010，2:33-39.

[12] 任学敏,万凝.用约化方法对有第三方担保的企业债券定价[J].同济大学学报,2009，7:989-992.

[13] 刘易,任学敏,花虹.考虑相关性的第三方担保价值的评估[J].同济大学学报,2013，3:465-469.