基于运行速度的公路线形协调性评价

唐秋生， 陈旭光

(重庆交通大学交通运输学院， 重庆 400074)

“十二五”以来，随着公路的大量建设，以及汽车保有量的高速增长，我国的交通安全形势日趋严重，有关资料表明[1]，近10年来，我国的公路交通事故死亡人数呈持续上升趋势.国内有关学者研究表明[2]，在“人-车-路-环境”系统中，由于道路原因造成的交通事故占据了总体事故的很大比重，仅次于驾驶员的因素.而在道路因素中，道路线形与车辆运行速度的不协调是重要组成部分.目前我国的公路设计理念主要是基于相应的国家与行业规范，首先在工可阶段预测交通量，确定公路的等级，进而确定设计速度.然后以在规划时确定的设计速度为核心参数，结合规范进一步确定平、纵、横等相关的几何设计参数[3].随着现代汽车性能的提高，驾驶员行驶时速度较快，而非一直遵循公路的设计速度.这种矛盾导致在实际情况中，车辆的运行速度与公路线形参数相脱节.特别是在线形指标比较低的路段，由于其对速度的敏感性较高，往往容易埋下事故隐患.对行驶的车辆构成极大的安全威胁.我国传统的公路设计理念，往往不能很好地适应现阶段的设计要求.因此，本文提出了基于运行速度进行公路线形设计的理念，并进一步应用运行速度的协调性与连续性，对已建成的公路线形进行安全性检验.以运行速度作为公路线形设计的核心参数，能更好地符合车辆行驶时的特点，从而在设计阶段减少可能的道路事故黑点，提高安全性.

1 典型路段运行速度的预测模型

1.1 运行速度的预测步骤

1)划分典型路段：典型路段是指弯坡组合、平曲线、纵坡、直线.划分标准如下：

直线段：R∈[1000，+∞],I∈(-3%,3%)

纵坡段：R∈[1000，+∞]∪I≤-3%

平曲线段：R∈1000∪I∈(-3%,3%)

弯坡组合段：R<1000∪I≤-3%

R<1000∪I>3%

以各个基本路段的起、终点，以及平曲线和弯坡组合段的中间点，作为运行速度预测的特征点.

2)根据划分后的典型路段，结合国家与行业规范，建立起相对应的初始运行速度预测模型.

3)结合研究路段的交通量、行车道、交叉口、平面视距等影响因素对初始运行速度进行修正，得到实际运行速度模型.本文主要针对小客车进行研究.

1.2 直线段运行速度预测模型

1)初始运行速度

本文中，初始运行速度采用表1[4]的推荐值.

表1 初始运行速度v0推荐值

2)直线段上的汽车行驶特性

在直线段，车辆一般会加速行驶至期望速度后不再增大，随后稳定在该速度行驶.

由此，推得直线段上运行速度模型为

(1)

式中：vs为期望车速(m/s)；v0为初速度(m/s)；a0为加速度(m/s2)；S为直线段的长度(m).

1.3 纵坡段运行速度预测模型

在纵坡段，当上坡时，由于重力、摩擦力等综合作用，车辆的运行速度会降低；当下坡时，车辆的运行速度会增加，但是驾驶员会刻意地控制速度保持在期望速度的范围.本文采用表2[4]中的推荐值对运行速度进行纵坡段的修正.

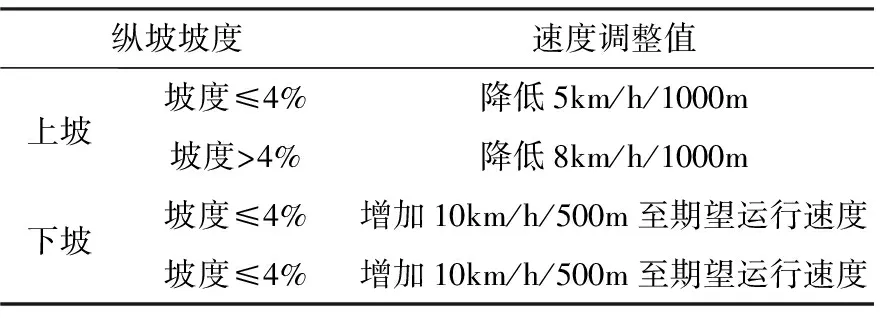
表2 纵坡的运行速度预测模型

1.4平曲线段运行速度预测模型分析与选取

平曲线段车辆的运行速度比较复杂.本文主要研究半径在1 000m以下的平曲线段.对于半径在1 000m以上的大半径的平曲线，考虑到其曲率的变化已经相当平缓，可以视为直线段进行研究[5].当汽车进入平曲线之前，汽车会减速，随后以固定的速度在平曲线上行驶.当驶离平曲线时，驾驶员会加速离开[6].

本文采用表3[4]中推荐的速度预测模型，根据曲线入口处的速度vin、当前曲线段的半径Rnow和上一个曲线段的半径Rback、曲线段中点速度vmiddle以及下一个曲线段的曲线半径Rfront来计算曲线段出口处的运行速度vout.

表3 平曲线的运行速度预测模型

1.5 弯坡组合段运行速度预测模型

作为纵坡和平曲线段的有机结合，弯坡组合段同时表现出两者的特征，但是又不是两者特征的简单叠加.本文研究平曲线半径小于1 000m的弯坡组合路段.

当汽车进入上坡曲线段时，会根据坡度的大小以及曲线半径的大小进行减速[7].当汽车离开上坡曲线段时，若下一路段的平曲线半径比较大，坡度比较小，则一般会适当地加速以弥补速度损失；反之，当前方路段的线形条件比较苛刻时，汽车往往会继续减速以适应苛刻的线形.

当汽车进入下坡曲线段时，除非前方的线形条件良好，否则一般不会有很明显的加速动作.一般而言，下一路段的线形指标越苛刻，汽车的减速动作越明显.

本文采用表4[4]对车辆在弯坡组合段的运行速度进行预测.

表4 弯坡组合段运行速度预测模型

表4中：R∈[120,1000]∪[2%，6%];vin,vmiddle,vout分别为进入曲线时的速度，变坡点或者曲线中点的速度，离开曲线时的速度；Rback,Rnow,Rfront分别为进入当前研究曲线段之前的曲线段半径，当前研究曲线段的半径，下一个曲线段的半径；inow1,inow2分别为当前研究曲线段的上一个和下一个路段的纵坡坡度值.

2 运行速度预测模型的修正

作为一个“人-车-路-环境”复合型的系统，道路交通系统的作用机理非常复杂.根据系统论的观点，系统中的各个要素在各自不同的数量级和权系数层面上发挥作用，同时彼此互相作用[8].这四个因素共同决定了系统的稳定性与安全性.同理，道路交通系统中，“人-车-路-环境”四个要素，每一个要素的特征发生变化时，都会直接作用于道路交通系统本身，即会导致系统安全性的改变.只有当这四个要素彼此适应、彼此协调时，才能保持道路交通系统的稳定，维持较好的安全状态.

而在车辆的实际运行状况中，理想的系统周边变量并不存在.以“人-车-路-环境”系统为例，前两者属于主观因素，可以人为地控制.而后两者属于非主观因素，无法人为地进行改变.车辆在运行时只能适应道路条件与环境条件，而车辆的运行速度也势必要因此发生改变.本文前面对运行速度进行预测时，仅仅推导出了理想状况下的速度模型，并没有考虑部分道路因素以及环境因素.因此，在研究车辆的实际运行速度时，必须将未考虑到的道路因素与环境因素加入进来，对前文得出的理想状况下的运行速度模型加以修正，进而得出更符合现实情况的实际运行速度模型.

2.1 交通量修正

根据交通流的相应理论，在道路上，服务水平随交通量的增大而降低，车辆的车头时距将从自由流时的泊松分布转而服从二项分布，车辆行驶自由度降低[9].换言之，由于周围车辆的影响，此时车辆的运行速度相比自由流时将受到干扰，发生变化.本文采用的交通量修正见表5.

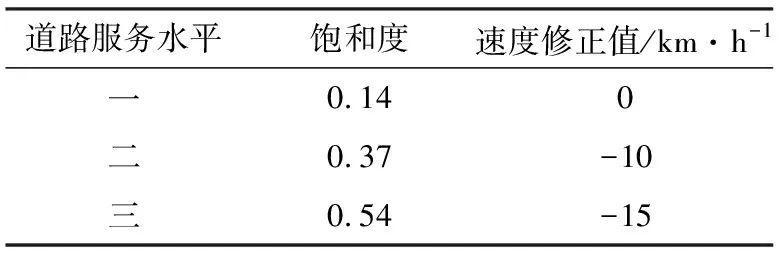
表5 交通量修正系数值Vv

2.2 路宽修正

在车辆行驶过程中，横向干扰也是必须考虑到的一个因素.横向干扰主要来自两个方面，一是不同车道之间的干扰，二是最外侧车道受到的路侧干扰.本文主要针对不同车道间的干扰进行研究.根据有关研究[3]，道路宽度对运行速度的影响如表6所示.

表6 路宽对速度修正值Vk

2.3 平面视距修正系数

当汽车在非直线段行驶时，平面视距对行驶的干扰非常大.特别是某些视距不良路段，是潜在的事故黑点，有很大的安全隐患.因此，要考虑平面视距对汽车运行速度进行修正.我国相应的国家和行业规范中高速公路、一级公路的平面视距以停车视距作为标准[3].

表7 平面视距对速度修正值Vs

2.4 交叉口修正

在公路的交叉口处，由于交通流分流与合流的存在，车辆的正常行驶会受到一定程度的干扰.本文中采用的交叉口修正系数见表8.

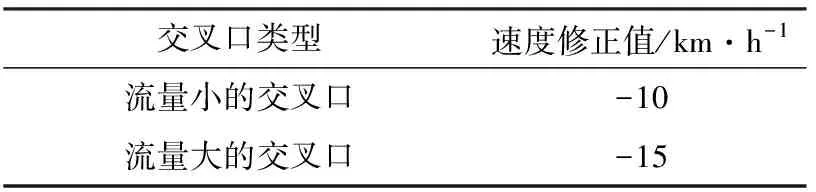
表8 交叉口对速度修正值Vj

2.5 实际运行速度预测模型

V实际=V0+Vs+Vk+Vj+Vv

(2)

式中：V实际为实际运行速度(km/h)；V0为理论运行速度(km/h)；Vs为平面视距修正系数(km/h)；Vk为路宽修正系数(km/h)；Vj为交叉口修正系数(km/h)；Vv为交通量修正系数(km/h).

3 基于运行速度的线形评价标准

公路线形的协调性也就是其平、纵、横线形的协调性[10].线形协调性良好的路段，车辆在行驶时，运行速度与线形指标相互协调，使得车速的过渡平稳、自然，没有车速突变的情况发生，从而提高了行车安全性.本文提出基于运行速度的线形协调性评价理念，应用运行速度的协调性与连续性，对已建成的公路线形进行安全性检验.

3.1 线形协调性评价标准

我国交通部的《公路项目安全性评价指南》推荐采用前后两个典型基本路段的运行速度间的差值|Δv85|作为评价指标，其标准见表9[4].

表9 线形协调性评价指标

3.2 线形连续性评价标准

学者Lamm等提出[11-14]设计速度和运行速度差值作为评价设计线形的标准见表10.

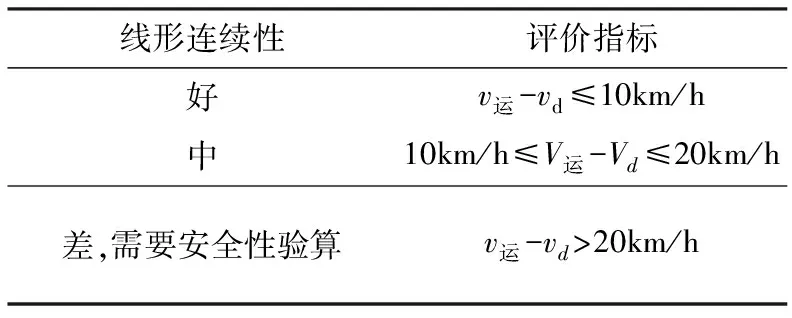
表10 线形连续性评价标准

本文主要采用上述两个标准对待评价公路路段的线形进行评价.

4 工程实例分析

本文选取的工程实例为黑龙江省鹤岗地区至辽宁省大连地区的鹤大高速公路G11杏山至复兴段.杏山至复兴(黑吉界)段为按照一级半幅设计施工的一级公路半幅，其中利用已建一级公路半幅扩建42.364km，新建7.95km.另建辅道113.14km，完全利用二级公路46.2km，新建二级公路23.84km，利用老路改建三级公路18.0km，新建三级公路15.3km，越岭段新建四级公路9.8km.根据工可阶段的交通量预测结果，主线全年平均交通量为 12 990～27 487pcu/d，辅道全年平均交通量为3 370～4 173pcu/d.扩建工程共设置互通立交 3座(另规划互通立交1座)，分离立交26座，增设服务区1处，停车区2处，匝道收费站3处[15].

本文评价路段的起点桩号K39+913.653，终点桩K49+713.653，全长约10km.该路段设计速度为80km/h，路基宽度为24.5m，有互通式立交一座.本文将K39+913.653至 K49+713.653共10km的路段划分为直线路段、纵坡路段、平曲线路段、弯坡组合路段四种类型共31个典型路段.

根据上文提出的运行速度修正模型，结合鹤大高速杏复段的实际工程特点，本文中鹤大高速杏复段运行速度预测的各项修正系数见表.

表11 鹤大高速杏复段运行速度各项修正值 km/h

根据上文提出的运行速度模型，参考鹤大高速杏复段的运行速度修正系数，对待鹤大高速杏复段的K39至K49待评价路段进行运行速度预测.得到的预测结果如图1所示.

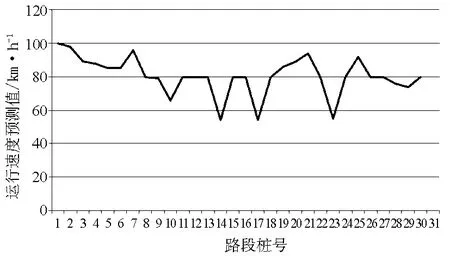
图1 运行速度预测值分布图

根据本文提出的基于运行速度的线形协调性评价标准，结合上文得出的运行速度预测值，对鹤大高速杏复段K39至K49段的公路线形进行安全性评价，并且提出相应的调整方案.得到的评价结果和调整方案见表12.

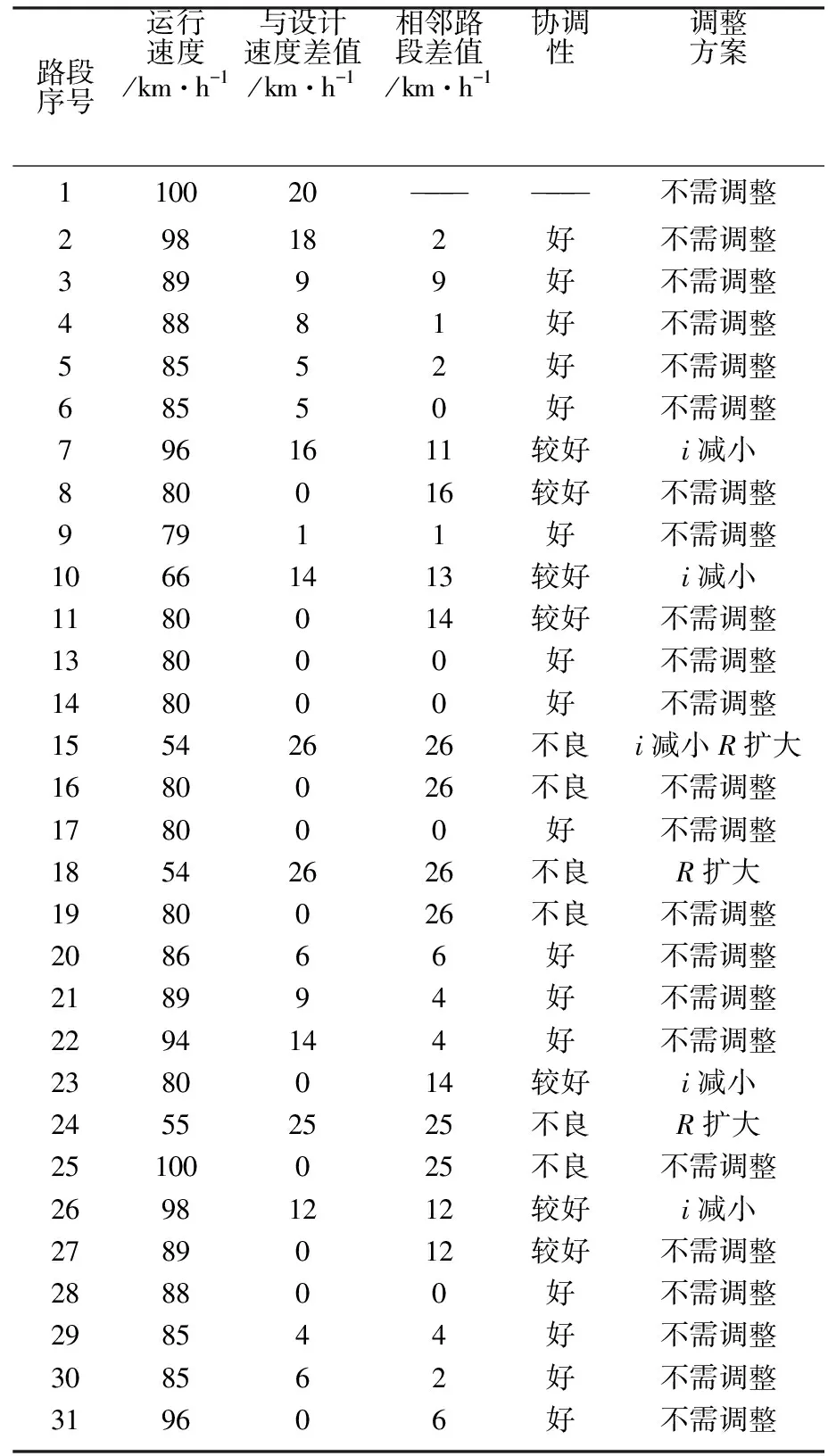
表12 公路线形协调性评价及调整方案

5 结束语

本文提出了基于运行速度的公路线形设计理念，结合有关规范和理想状况下的运行速度预测模型，考虑交通量、视距等实际因素，对运行速度预测模型进行了相关的修正，得到了车辆实际运行情况下的运行速度预测模型.总结了基于运行速度的公路线形协调性和连续性评价标准.对拟建公路的线形设计以及建成公路的线形安全性检验有一定的指导意义.实际上对道路设计进行更准确、全面的评价，还需要加入运行速度和周围环境，如噪声污染、水环境污染等这些指标.

[1] 公安部交通管理局.中华人民共和国道路交通事故统计年报(2010年度)[R].北京:公安部交通管理科学研所,2011.

[2] 高建平.高速公路运行车速研究[J].重庆交通学院学报,2004,23(4):78-81.

[3] JTG D20-2006公路路线设计规范[S].北京:人民交通出版社.

[4] JTG/T B05-2004公路项目安全性评价指南[S].北京:人民交通出版社,2004.

[5] 隋晓飞.基于运行速度的高等级公路线形评价及改善措施[D].西安:长安大学,2012.

[6] 魏军.基于运行速度的公路几何线形优化设计探讨[J].北方交通,2011(4):43-46.

[7] 唐忠国.高速公路行车速度与行车安全性分析研究[J].公路交通科技(应用技术版),2011(5):257-258.

[8] 卓祖城,程昊,李勃.采用运行速度检验公路线形设计的应用研究[J].道路工程,2012(9):198-201.

[9] 金增曲珍.运行速度与公路线形连续性研究[D].成都:西南交通大学,2010.

[10] 贺玉龙,卢仲贤,马国雄.高速公路直线段车辆稳定运行速度[J].公路,2002(10):99-103.

[11] 李伟.公路路线-汽车运行响应模型的研究[D].西安:长安大学,2002.

[12] Lamm R,Choueiri E M,Mailaender T.Comparison of operating speed on dry and wet pavement of two lane highway[C]//Transportation Research Record 1280, TRB.Washington,1990.

[13] Mbroz A.3D road traffic situation simulation system[J]. Advances in Engineering Software, 2005,36:77-86.

[14] 屠书荣,吴敏刚,程永华.基于道路和环境条件的干线公路安全性评价方法[J].重庆交通大学学报：自然科学版, 2010,29 (3):46-50.

[15] 魏显威.鹤大国家高速公路宁安至复兴(黑吉界)段扩建工程环境影响评价公众参与信息公告[EB/ O L]. (2008-7-16) [2014-4-16]. http://www.hljjt. gov.cn /tongzhigonggao/document.2008-07-16.6022067390.