圆弧输流管道流固耦合力学特性分析

张毅鹏 侯建华 宋贝贝 王娇

郑州大学力学与工程科学学院（450001）

圆弧输流管道流固耦合力学特性分析

张毅鹏 侯建华 宋贝贝 王娇

郑州大学力学与工程科学学院（450001）

基于流固耦合理论，建立了1/4圆弧管道与内部流体三维流固耦合有限元模型，计算并分析了管道力学特性。计算结果表明，最大主应力出现在管道底部的固定端附近横向摆动较大的一侧，且随着流体提升速度的增加而增加，最大横向摆动的发生位置在1/4圆弧的中间点，该位置处内部流体冲力效应较为明显，建议加强弯管转折处的摆幅监控。

流固耦合；弯管道；有限元；内部流

管道输流问题是学术界研究的热点课题之一。在一些具有简单形状的输流管道（如两端固定的较短直管等）分析中，流固耦合研究有大量报道。1952年，Housner根据Hamilton[1]原理首次推导出含有稳定内流均匀直管的动力学方程，在此基础上加入管道变形对流体的影响，形成了管道流固耦合振动方程[2-3]。王世忠[4-6]等根据Hamilton原理，采用有限元方法,推导输流管道流固耦合振动方程，得到反对称的流固耦合阻尼矩阵和对称的流固耦合刚度矩阵。许多学者采用ADINA软件壳单元和四面体单元分别离散管道壁和内部流体，建立有限元模型[7-9]，王永辉在系统地分析三种有限元格式的流固耦合方程优劣性的基础上,基于位移-位移格式的流固耦合方程，导出了三维几何非线性流体单元的切线刚度矩阵计算公式，并编制了相关程序。该试验拟建立两端简支或固支结构层状管道,研究在自重作用下，管道与内部流的力学特性影响规律。

1 流固耦合动力学方程

流固耦合系统的控制方程包括流体区域基本方程、固体区域基本方程以及流固交界面边界条件。

1）流体区域基本方程：

其中：uf和分别为流体位移和速度，ff、ρf、pf和μ分别为单位质量流体力、流体密度、流体压力和黏性系数,▽，▽2分别为哈密顿算子和Laplacian算子。

2）固体区域基本方程：

其中：M、C、K分别为软管的质量、阻尼、刚度,us、分别为软管的位移、速度、加速度，ΣF为软管受到的外力（包括内外部流体作用力、浮力块浮力、自身重力等）。

3）流固交界面边界条件：

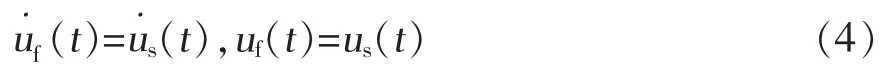
将式（1）～（4）进行有限元离散并联合求解，即可得到软管的流固耦合位移和应力解。

2 有限元模型

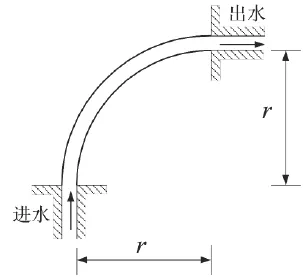
图1 受力模型示意图

以一段圆弧形管道为研究对象（如图1所示），管外径为20mm，管内径为15mm，，半径r为0.1m，建立管道与内部流体三维流固耦合模型，其中管道部分采用固体三维八节点六面体单元，共640个单元,内部流体采用流体三维八节点六面体单元，共3200个单元，具体网格划分见图2，固体与流体在接触面上共用节点，满足位移与应力连续条件。考虑管内流体为液固两相流，为了更好地模拟管道实际工作情况，试验假设管内流体为含沙水流（宾汉流体）。流体运动黏滞系数和屈服应力是宾汉流体两个重要的物性参数,均与内部流的体积浓度Cv密切相关，可以表述为：

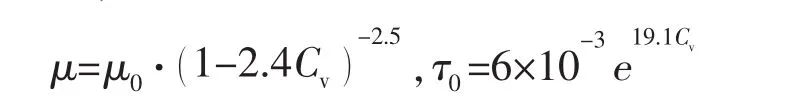
其中：μ0为运动黏滞系数,取μ0=1.792×10-3m2/s。

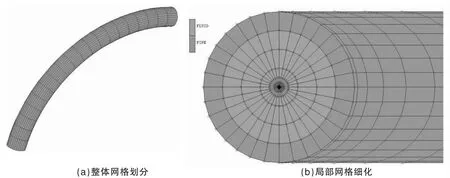
图2 有限元模型

图3 管道最大主应力云图

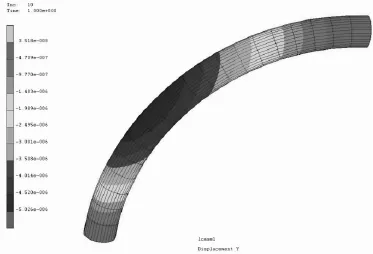
3 结果与分析

图3为管道最大主应力云图。可见，当向上提升流体时，管道底部的固定端附近出现应力集中，且最大主应力出现在横向摆动较大的一侧，随着流体提升速度的增加,最大主应力也随之有所增加，但整体而言,流体冲力对最大主应力的影响有限。相比较直管，弯管在底部的最大主应力明显较大，当采用弯管进行输送流体时，应对固定端的稳定性进行验算。

图4为整体管道横向摆动幅度云图。可见，最大横向摆动的发生位置在1/4圆弧的中间点，该处是弯管内流体提升方向改变较大的点，在该位置以下处，流体主要偏向于向上提升，而经过该位置后，流体向水平方向输送的趋势加强,因此在该位置处，内部流体冲力效应较为明显。建议在考虑弯管输送流体时，应加强弯管转折处的摆幅监控，以保证输送的安全与稳定。

4 结语

基于流固耦合理论，建立了圆弧管道与内部流体三维流固耦合有限元模型，该有限元模型能较好地模拟实际管道输流过程中的流固耦合效应，计算结果较好地显示了管道的力学特性。最大主应力出现在管道底部的固定端附近横向摆动较大的一侧，且随着流体提升速度的增加而增加。最大横向摆动的发生位置在1/4圆弧的中间点，该位置处内部流体冲力效应较为明显，建议加强弯管转折处的摆幅监控。

[1]Housner G W.Bending Vibrations of a Pipe Line Containing Flowing Fluid[J].ASME Journal of Appliedmechanics, 1952,19:205～208.

[2]Handelman G H.A Note on the Transverse Vibration of a Tube Containing Flowing Fluid[J].Quarterly of Appliedmathematics,1955,13:326～329.

[3]Herrmann G.Bungay R W.On the Stability of Elastic Systems Subjected to Nonconservative Forces[J].Appl.mech,1964,31:435～440.

[4]王世忠,王茹.三维管道固液耦合振动分析[J].哈尔滨工业大学学报,1992,22(4):43～49.

[5]王世忠,刘玉兰,黄文虎.输送流体管道固-液耦合动力学研究[J].应用数学与力学,1998,29(11):987～993.

[6]王世忠,于石声,赵阳.流体输送管道的固-液耦合特性[J].哈尔滨工业大学学报,2002,34(2):241～244.

[7]蒋录珍.动荷载作用下地下管道破坏的数值模拟[D].河北:河北理工大学,2006.

[8]张骞,张世富,张起欣,朱金鹏.海上漂浮式输油管线内部流体流速引起管线变形的研究[J].管道技术与设备,2007(4): 1～2.

[9]杨章锋.内流对海底悬跨管线管壁应力影响的数值研究[D].大连理工大学,2008.

国家级大学生创新实验计划项目（1210459092）