单摆力学参量转电磁参量的对比性研究

罗金华，王昆林

(楚雄师范学院物理与电子科学学院，云南 楚雄 675000)

在电路中，若改变电路中电阻阻值的大小，会使电路中电流的大小发生变化，从理论上讲，如果电路中电阻的阻值呈周期性变化，那么电路中的电流也应该呈周期性变化。由于单摆的振动是简谐振动，为了使实验更为简单明了，采用单摆来代替滑线变阻器的滑片，单摆摆动时电路中的电阻会发生周期性变化，从而使电路中的电流也发生周期性变化。采用DIS数字化信息测量系统对各参量进行测量，将力学机械振动参量与电磁学电磁参量进行牵连式对比研究。

1 原理及实验装置

实验原理电路如图1所示，使用金属丝做单摆的摆线，在金属摆球下端安装一根针，在单摆下端放一个装有水的水槽，单摆摆动时，摆球下端的针在水中随摆球一起摆动，针在水中运动时，水对针的阻力很小，可以忽略，这样，单摆和水槽就相当于一个电阻阻值周期性变化的滑线变阻器。

实验原理图如图2所示，可以证明，电流I3是时间t的周期函数。为了简单起见，忽略电源内阻，因电位器只是起到调零作用，可以取零。令:

图1 实验装置图

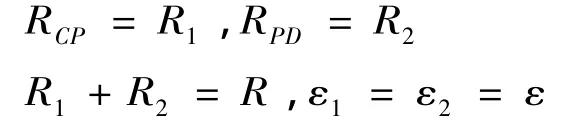
对于节点H:I1=I2+I3

对于回路ABPHA:I1R1+I3RG=ε

对于回路HPEFH:I2R2－I3RG=ε

由上述方程组可以解得;

再令:

从(1)式可以看出，若滑片P在CD上做简谐振动，则:

将(2)式代入(1)式得:

图2 实验原理图

由(3)式可以看出，电流I3是关于时间t的周期函数，其周期为，与滑片P的运动周期相同，因为，所以通过RG的电压UG的周期与电流I3的周期相同，测出通过RG的电压UG就可以电流I3。

对于单摆，可以证明其振动周期T满足下式:

通过DIS数字化信息测量系统测量到电压UG，并使其数字化，图像化，从而可进行参量牵连比较性研究。

2 实验研究

2.1 水槽中无水时的实验研究

用一根长l=74.50cm的金属丝，直径d=1.00cm的摆球，水槽中不放入水，按照图1组装好后，拉开摆线，使摆线与竖直方向成5°角，并使单摆振动起来，启动DIS系统，传感器检测到变量，数据采集器采集数据经计算机处理后，绘出图线，见图3。

由图3可以看出，当水槽中无水时，通过RG的电压恒为零，即通过RG的电流恒为零，这是由于水槽中无水时，整个电路相当于断路，所以通过RG的电流恒为零。

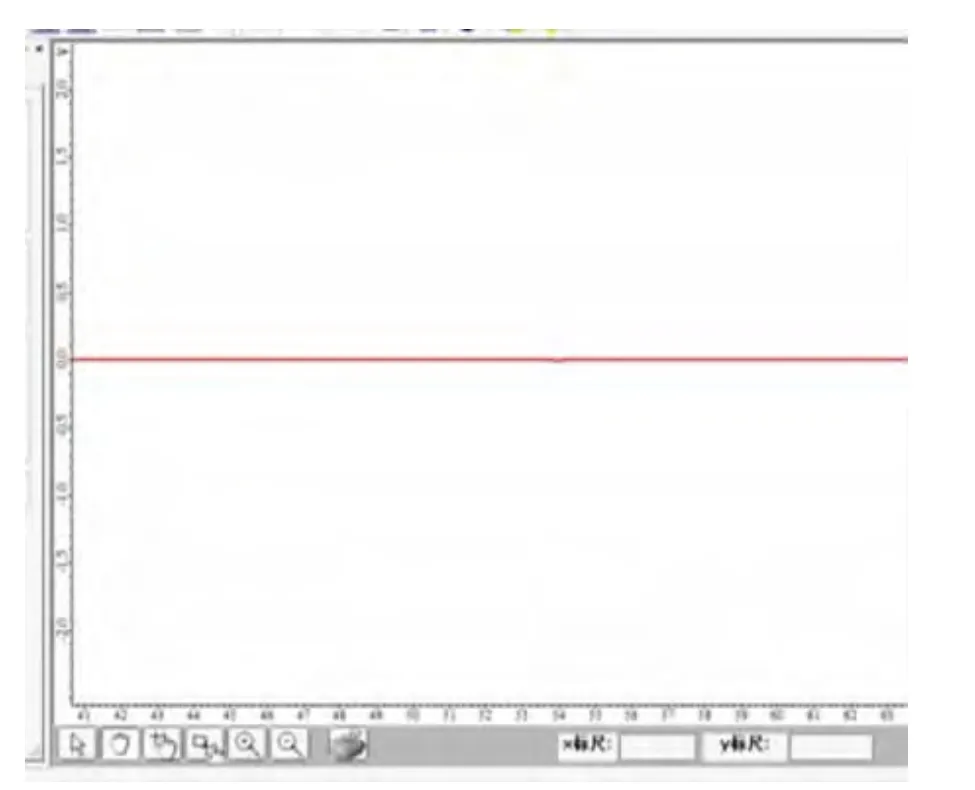
图3 水槽中无水时的U－t图

2.1.1 水槽中无水时单摆的周期研究

用一根长l=74.50cm的金属丝，直径d=1.00cm的摆球，水槽中不放入水，按照图1组装好后，拉开摆线，使摆线与竖直方向成5°角，并使单摆振动起来，用秒表测得单摆的振动周期T=1.70s，根据(4)式可以计算出理论值t0=1.74s。

两者相差△T=T0－T=0.04s，两者相差很小，可忽略。

2.2 水槽中有水时的实验研究

用一根长l=74.50cm的金属丝，直径d=1.00cm的摆球，水槽中放入一定的水，按照图1组装好后，拉开摆线，使摆线与竖直方向成5°角，并使单摆振动起来，启动DIS系统，传感器检测到变量，数据采集器采集数据经计算机处理后，绘出图线，见图4。

由图4可知，通过RG的电压与时间t成余弦关系，即，通过RG的电流也是与时间t成余弦关系，和(3)式是一一对应，由此可知，其单摆振动的机械振动参量与相应的电磁参量也是一一对应的。

图4 水槽中无水时的U－t图

2.2.1 水槽中有水时单摆的周期研究

由图4可以读出，当水槽中有水时，单摆的振动周期T=1.77s，当水槽中无水时，单摆的振动周期T=1.70s。

两者相差△T=0.07s，说明水对针存在阻力，但此力十分微弱，可以忽略。

2.3 水槽中有水时单摆以不同角度振动时的实验研究

用一根长l=74.50cm的金属丝，直径d=1.00cm的摆球，水槽中放入一定的水，按照图1组装好后，拉开摆线，使摆线分别与竖直方向成1.5°、3°角，并使单摆振动起来，启动DIS系统，传感器检测到变量，数据采集器采集数据经计算机处理后，绘出图线，见图5、图6。

图5 水槽中有水时单摆以1.5°幅角振动的U-t图

图6 水槽中有水时单摆以3°幅角振动的U-t图

由图5、图6可知，通过RG的电压与时间t成余弦关系，即通过RG的电流也是与时间t成余弦关系，和(3)式是一一对应，由此可知，其单摆振动的机械振动参量与相应的电磁参量也是一一对应的。

2.3.1 水槽中有水时单摆以不同角度振动时的周期研究

由图5可以读出，当水槽中有水，单摆以3°幅角振动时的周期T=1.76s，由图6可以读出，当水槽中有水，单摆以3°幅角振动时的周期T=1.76s，而，由图4可以读出，当水槽中有水时，单摆的振动周期T=1.77s。

可以看出周期的大小与单摆振动时的幅角无关，与(4)式吻合。

2.3.2 水槽中有水时单摆以不同角度振动时的电压峰值的研究

由图4、图5、图6可以看出，通过RG的电压的峰值随振动幅角的增大而增大，即通过RG的电流的峰值随振动幅角的增大而增大。这是由于当单摆以不同幅角振动时，针划过水的范围不同，相当于滑线变阻器阻值的范围不同，影响了通过RG的电流的峰值，与(3)式吻合。

3 结束语

由上可见，将单摆做机械振动的各参量转换为电磁参量，用DIS系统进行测量，每一机械振动参量能与相应的电磁参量一一对应，将对机械振动的研究转为电磁振动的研究，参数的测定更加方便准确，分析研究起来更加方便准确，同样可将这一种转换为电磁参量的方法推广到其他物理量的测量上。

［1］漆安慎，杜婵英.普通物理力学 ［M］.北京:高等教育出版社，2005.6.

［2］梁灿彬，秦光荣，梁竹健.普通物理电磁学［M］.北京:高等教育出版社，2004.5.

［3］樊伏云，庞捷.关于简谐振动的能量问题 ［N］.中州大学学报，1994，(04).

［4］刘进京，直流变交流的简易方法 ［R］.《教育实践与方法研究》，2001，(08).

［5］赖俊池，直流电变交流电演示模型的研究与制作 ［A］.第六届全国高等学校物理实验教学研究会论文集 (下)［C］.2010.