硅纳米晶体薄膜热膨胀性质的分子动力学研究

黄建平，杨 程，胡诗一，阳 波

（湖南师范大学计算机部量子结构与调控教育部重点实验室，长沙410081）

1 引 言

硅纳米晶体薄膜作为微纳电子器件和微纳机电系统中最常用的衬底材料，其热膨胀性质的研究具有非常重要的意义：一方面硅纳米晶体薄膜与其他薄膜热膨胀系数的失配会产生热应力，而较大的热应力会引起系统的失效或损坏；另一方面，硅纳米晶体薄膜的热膨胀也能成为微热执行器的动力来源.由于硅纳米晶体薄膜的尺寸很小，对其热膨胀性质进行实验测量将非常困难.运用分子动力学 （MD），可以通过数值求解牛顿运动方程得到原子位置和速度等随时间变化的信息，在此基础上得到材料的热学性质.分子动力学是沟通微观与宏观的桥梁，是研究热学性质的一种非常有用的理论工具，目前已被成功地运用于纳米晶体薄膜的熔化性质、比热和热传导研究［1-3］，然而还未见过用于纳米晶体薄膜的热膨胀性质研究的报导.在硅纳米晶体薄膜理想的 （100）表面，每个原子有两个空键，空键的存在使表面相邻的Si原子之间相互吸引，而有可能形成新的共价键，发生二聚，从而使表面重构［4-5］，并最终对其热膨胀性质产生影响.本文将用分子动力学方法研究表面原子二聚对硅纳米晶体薄膜热膨胀性质的影响.

2 硅纳米晶体薄膜的分子动力学模拟

我们选用了由美国Sandia国家实验室开发的、开源免费的LAMMPS 软件［6］，在八核计算机上对硅纳米晶体薄膜进行分子动力学的并行模拟计算.

由于相对于其它势函数，S-W 势函数能够较好地重现块体硅单晶的熔点、热传导系数等热学参数［7］，因此我们选择了S-W 势.硅纳米晶体薄膜中原子的初始位置按其晶体结构给出，初始速度由设定温度下的Maxwell-Boltzmann分布随机选取；薄膜面向安排10×10个原胞，采用周期性边界条件，薄膜法向安排10层原胞.系统为等温等压（NPT）系综，采用恒零压，对不同温度下的硅纳米晶体薄膜进行分子动力学模拟，时间步长为1.0×10-15s，先用1.0×106步进行弛豫以达到热力学平衡，再用0.5×106步获取所有硅原子的位置与速度随时间的演化.通过在热力学平衡状态下对各个原子所有不同时刻的位置坐标值求平均，可以求得硅纳米晶体薄膜中各个晶面的位置，并进而求得相应晶面间距，也能计算出晶格常数.硅纳米晶体薄膜的热膨胀系数可定义为：

其中L 表示硅纳米晶体薄膜面向的晶格常数a或晶面间距d.

3 温度的量子化修正

在分子动力学模拟中，根据Boltzmann统计，分子动力学温度可由以下计算公式得到：

其中，＜…＞表示平均值，TMD表示分子动力学温度，各个i表示不同的原子.由此得总的晶格振动内能与分子动力学温度的关系为：

然而以上公式只有在量子效应可以忽略的情况下才成立，即要求温度远大于Debye温度，在一般情况下，需要对分子动力学温度进行量子化修正.

在固体量子理论中，晶格振动内能可表示为：

其中，ω 是声子角频率，ρ（ω）是声子谱密度，n（ω，T）是声子在绝对温度T 下的布居数：

定义速度自相关函数［8］：

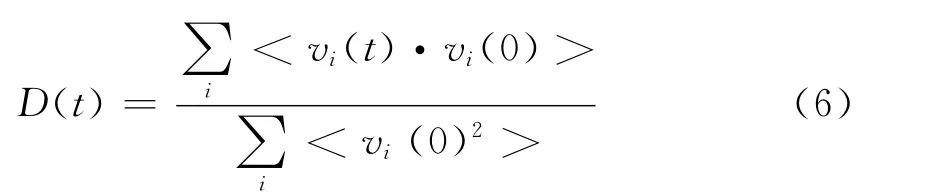
声子谱密度可由速度自相关函数D（t）进行Fourier变换得到［8］：

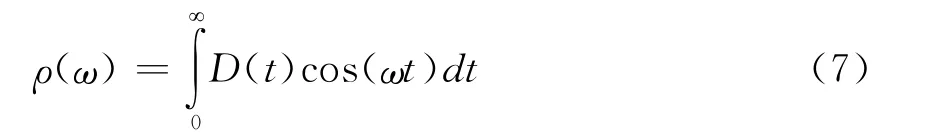
结合（3）式及 （4）式，则有：

∞

根据 （8）式，即可将分子动力学温度TMD转化为绝对温度T，从而进行温度修正.

4 结果分析与讨论

为了将硅晶体薄膜材料和块体材料的热膨胀性质进行对比，首先对其块体材料进行MD 模拟.安排10×10×10个原胞，在三维方向上均采用周期性边界条件，其它模拟参数与条件设置同纳米晶体薄膜，模拟得到各不同温度下块体硅晶体的晶格常数，再对这些数据进行拟合，并对分子动力学温度进行修正，得到块体硅晶体的晶格常数随温度的变化关系曲线，有关结果如图1所示.根据块体硅晶体的晶格常数随温度的变化关系，得到如图2所示的硅块体材料热膨胀系数随温度的变化关系，所得结果与Wei等人［9］的实验测定值、Noya等人［10］基于Feynman路径积分的MC 模拟结果以及黄建平等人［11］晶格动力学方法的计算结果吻合.这说明分子动力学模拟是能用于热膨胀性质的研究并得到正确结果的.

图1 硅块体材料晶格常数随温度变化Fig.1 The lattice constant of Si bulk crystal vs temperature

图2 硅块体材料热膨胀系数随温度变化Fig.2 The thermal expansion coefficient of Si bulk crystal vs temperature

同样对硅纳米晶体薄膜热膨胀性质进行模拟，得到热平衡状态下其面向晶格常数和热膨胀系数随温度的变化关系分别如图3和图4所示.由图可知，与块体材料相比，硅纳米晶体薄膜热的膨胀性质明显不同，主要体现为：在约400K 以下的低温段，随着温度的升高，硅纳米晶体薄膜的面向的晶格常数反而减小，而相应的热膨胀系数为负值.目前还未见文献对该奇异现象有过报导.

一般地来讲，热膨胀是由原子之间的非和谐势能引起的，在低温时非和谐势能较小，而在高温时非和谐势能较大，因此温度的升高热膨胀增加，即一般材料都呈现正的热膨胀.纳米硅晶体薄膜热膨胀的奇异性质的存在肯定有基于其物质结构的内在原因.

图3 硅纳米晶体薄膜晶格常数随温度变化Fig.3 The lattice constant of Si nanocrystal film vs temperature

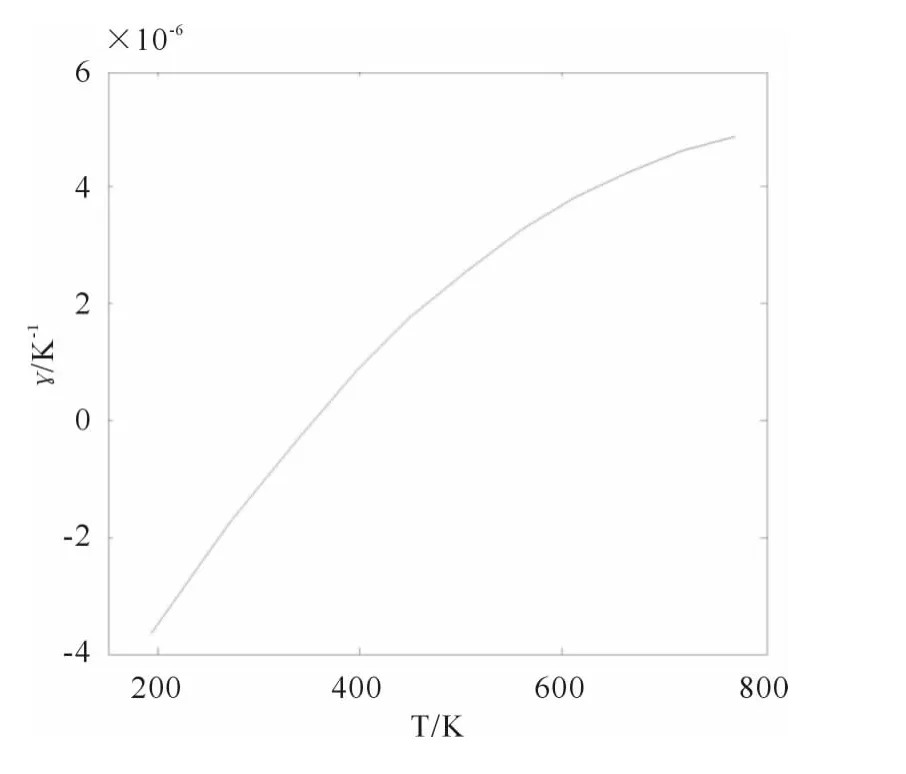
图4 硅纳米晶体薄膜热膨胀系数随温度变化Fig.4 The thermal expansion coefficient of Si nanocrystal film vs temperature

纳米硅晶体薄膜的每个内部硅原子的4 个SP3杂化轨道与周围4个硅原子提供的4个SP3杂化轨道形成4个共价键，而纳米硅晶体薄膜的每个表面硅原子只与次表面原子的形成2个共价键，另外在薄膜表面的外侧还存在2个空键.在热运动加剧的情况下，这些表面原子有可能在某个瞬间相互接近而使其空键对应的SP3杂化轨道有部分重叠，形成新的共价键，并使这些形成新的共价键的原子之间的距离缩短，从而使表面发生重构，这被称为二聚现象［4-5］.块体硅晶体的比表面积很小，其表面原子的二聚对热膨胀性质的影响较小，可以忽略；而纳米硅晶体薄膜的比表面积很大，其表面原子的二聚对热膨胀性质的影响较大，必须加以考虑.

我们对处于不同温度下的硅纳米晶体薄膜表面层的二聚原子数目进行统计，发现在约400K 以下的低温段，随着温度的升高薄膜表面层的二聚原子数目增加较多；而在约400K 以上的高温段，由于表面原子中二聚的原子份额已经很大，再升高温度虽然还会增加二聚原子数目，但增幅不会很大，并逐渐趋于饱和.于是在低温下，随着温度的升高，由二聚现象而引起的晶格常数减小要比由原子之间的非和谐势能引起晶格常数的增加要来得严重，从而导致硅纳米晶体薄膜面向的晶格常数随温度增加而减小，故呈现负热膨胀系数；而在高温下，由原子之间的非和谐势能引起的晶格常数的增加要比由二聚现象而引起的晶格常数减小要来得多，从而导致硅纳米晶体薄膜面向的晶格常数随温度增加而增大，故整体呈现正热膨胀系数.

［1］ Yang X，Wu D.The melting behaviors of the Nb（1 1 0）nanofilm：a molecular dynamics study［J］.Appl.Surf.Sci.，2010，256（10）：3197.

［2］ Adiga S，Adiga V P，Carpick R W，et al.Vibrational properties and specific heat of ultrananocrystalline diamond：molecular dynamics simulations［J］.J.Phys.Chem.C，2011，115（44）：21691.

［3］ Ju S，Liang X.An atomic level study on the out-ofplane thermal conductivity of polycrystalline argon nanofilm［J］.Chin.Sci.Bull.，2012，57：294.

［4］ Battaglia C，Gaál-Nagy K，Monney C，et al.Elementary structural building blocks encountered in silicon surface reconstructions［J］.J.Phys.：Condens.Matter，2009，21（1）：013001.

［5］ Fauster T，Tanaka S，Tanimura K.Unoccupied dimer-bond state at Si（001）surfaces［J］.Phys.Rev.B，2011，84：235444.

［6］ Plimpton S.Fast parallel algorithms for short-range molecular dynamics［J］.J.Comp.Phys.，1995，117：1.

［7］ Stillinger F H，Weber T A.Computer simulation of local order in condensed phases of silicon［J］.Phys.Rev.B，1985，31：5262.

［8］ Yu J.Fabrication of Microcalorimeter and Investigation on the Specific Heat of Micro／nanometer Thin Films［D］.Dalian：Dalian University of Technology，2006（in Chinese）［余隽.微量热计的研制及微纳米薄膜比热测试与分析［D］.大连：大连理工大学，2006］

［9］ Wei S，Li C，Chou M Y.Ab initio calculation of thermodynamic properties of silicon［J］.Phys.Rev.B，1994，50：14587.

［10］ Noya J C，Herrero C P，Ramirze R.Thermodynamic properties of c-Si derived by quantum path-integral Monte Carlo simulations［J］.Phys.Rev.B，1996，53：9869.

［11］ Huang J P.Lattice dynamics study on thermal properties of crystal film in MEMS ［D］.Changsha：National University of Defense Technology，2008（in Chinese）［黄建平.MEMS晶体薄膜构件热学性质的晶格动力学研究［D］.长沙：国防科技大学，2008］