氢分子离子库仑爆炸中核动力学的理论研究
2014-03-20张彩萍施昊霆苗向阳
张彩萍,施昊霆,苗向阳
(山西师范大学物理与信息工程学院,临汾041004)
1 引 言
随着强激光技术的发展,激光与原子分子相互作用已经成为人们研究的一个热点[1,2].实验表明在超强超短激光脉冲作用下,原子分子会出现一系列用微扰理论无法解释的新现象,而由强激光与分子相互作用引起的分子解离和电离也恰恰能基于这些有趣的新现象去解释,例如键的软化[3]、键的硬 化[4]、阈 上 解 离[5]和 电 荷 共 振 增 强电离[6]等.在这些现象中,电荷共振增强电离引起了人们的广泛关注.在实验上,人们可以通过研究动能释放谱进而阐明这些新奇现象的物理机制,而动能释放谱的结构特征,如谱的信号强度和谱的峰值位置对强激光脉冲的峰值强度、脉冲持续时间、脉冲形状和波长是非常敏感的[5,7,8].
许多相关的实验都是基于中性的H2分子的,这样就使得研究更加复杂[9,10].幸好在一些实验中,人们可以用Franck-Condon(FC)分布产生离子束(H+2),并且通过研究解离动能谱和库仑爆炸谱的多峰值结构,发现了更多有趣的现象和结果[7,8,11-13].
在原则上,这些动力学的理论模拟需要精确求解含时薛定谔方程.大量的理论研究都使用了Born-Oppenheimer(B-O)近似条件,也就是将核的运动从电子的运动中分离出来.使用B-O 近似条件是很难得到精确的结果的,因为强激光场很可能影响的库仑势,因此,为了得到更加准确的结果,必须同时考虑核和电子的全维度运动.但为了简单却又不失这些现象的动力学本质,本文采取了一些合理的近似并使用了一维含时薛定谔方程进行理论模拟.
在本文中,我们通过数值求解非B-O 近似条件下的一维含时薛定谔方程,理论模拟了的库仑爆炸核动能释放谱,并通过研究分析处于不同初始核振动态下时动能释放谱的峰值位置的变化阐明了H+2在库仑爆炸通道中发生电荷共振增强电离时的核动力学.
2 理论方法
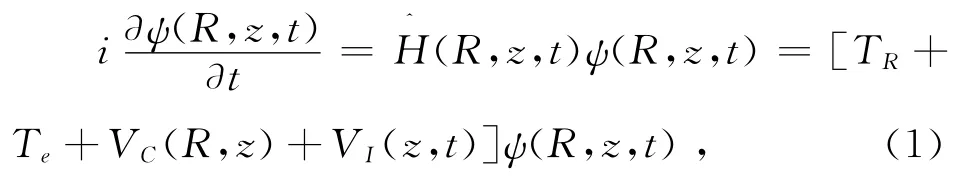

波函数随时间的演化使用了标准的二阶劈裂算符方法[17]:

为了得到核动能释放谱,我们使用了流算符和虚拟探测方法[18].无特别说明本文均使用原子单位.
3 结果和讨论

图1 氢分子离子在不同初始振动态下的库仑爆炸核动能释放谱.激光参数为:I= 7.0×1013 W/cm2,波长λ=800nm,半宽τ=100fsFig.1 The Coulomb explosion kinetic-energy-release spectra of H+2 in various initial vibrational states.The laser parameters are:I=7.0×1013 W/cm2,λ=800nm,τ=100fs
为了阐明图1中谱峰值位置变化的不同趋势出现的物理机制,图2 (a)和图2 (b)分别给出了氢分子离子的初始核振动态为低振动态和高振动态下的与核间距R 有关的电离速率 (Ionization rate)分布图.众所周知,在分子与强激光作用过程中,电离速率最大处往往会发生电荷共振增强电离,其相应的核间距称之为关键或临界核间距(Rc).在图2 (a)中,最大电离速率所对应的R几乎是一样的,也就是说,对于低振动态,发生电荷共振增强电离的Rc是相等的,数值为8.6a.u..在的库仑爆炸通道中,分子离子首先会被强激光激发到解离态发生解离,此时核会获得一定的动能:Ediss= (hv-|Ev|),接着剩下的带正电的两个H原子核会在库仑作用的影响下相互排斥直到Rc发生库仑爆炸,所以动能释放谱中的核动能应该等于E=Ediss+e2/ (Rc).对于相对较低的振动态来说,由于Rc相等而且随着振动态的增加,Eu的绝对值是随之减小的,这就导致Ediss增大,E 相应增大,体现到核动能谱中就是峰值位置会向高能量区域移动.然而,在图2 (b)中,Rc的位置会随着振动态的变化而发生明显的变化,具体来说:Rc的值会随着振动态的增加而增加 (v=6时,Rc=6a.u.;v=7 时,Rc=7a.u.;v=8 时,Rc=10a.u.),因此不能简单地使用E= Ediss+e2/(Rc)来解释图1中相应的峰值位置的移动.重新考虑的库仑爆炸通道过程,我们可以将分子离子在解离态上的运动等效简化成氢分子离子在一个中间态上的运动,对于相对较低的振动态来说,核波包在基态时本身能够运动的R 范围很小,这使得它们在被激光激发到中间态上后要运动更长的时间到达Rc进而发生电荷共振增强电离,在此过程中,核波包在中间态上获得的能量相对于在电离态 (1/Rc)上获得的能量是不可忽略的,而对于高振动态,核波包在基态运动本身的R 范围很大,这使得它们在被激光激发到中间态上后没有必要运动很长的时间就会到达Rc并发生电荷共振增强电离到达电离态,在此过程中,核波包在中间态上获得的能量相对于在电离态上获得的能量是可忽略的,也就是说在此情况下,核的动能大部分是依赖于1/Rc(eV)的.所以可以用1/Rc(eV)去估算高振动态动能释放谱中的峰值位置.在图2 (b)中,随着振动态的增加,Rc随之增加,1/Rc相应减小,这就导致核动能释放谱中的峰值位置向低能量区域移动.此外可以验证,1/Rc(eV)的值和图1中高振动态的谱峰值所对应的动能值符合的很好.具体地说:当v=6时,1/Rc(eV)=4.5eV,E=4.7eV;当v=7 时,1/Rc(eV)=4.0eV,E=4.0eV;当v=8 时,1/Rc(eV)=2.7eV,E=2.8eV.在图2中还应该注意的是无论对于低振动态还是高振动态,分子离子的电离都是发生在一定范围的核间距内的,只是对于低振动态来说,此范围大致相同,而对于高振动态来说,此范围有随着振动态的增加而增加的趋势.

图2 氢分子离子处于不同初始核振动态下的电离速率随核间距R 变化的分布图:(a)低振动态 (v=2,3,5);(b)高振动态 (v=6,7,8)Fig.2 The R-dependent ionization rate of H+2 for various initial vibrational states.(a)low vibrational states(v=2,3,5);(b)high vibrational states(v=6,7,8)
4 结 论
本文通过数值求解非B-O 近似条件下的一维含时薛定谔方程理论模拟了H+2分子离子处于不同初始核振动态时的库仑爆炸核动能释放谱.理论模拟结果表明:当初始振动态是相对较小的振动态时,谱峰值会随着振动态的增加向高能区域移动,相反地,当初始振动态是相对较大的振动态时,谱峰值会随着振动态的增加向低能区域移动.文中合理解释了不同初始振动态下谱峰值移动的物理机制,将H+2发生库仑爆炸时的核动能与核间距R 之间建立了一一对应关系,使得利用库仑爆炸核动能释放谱去重现分子离子的核动力学成为可能.
[1] Giusti-Suzor A,Mies F H,DiMauro L F,et al.Dynamics ofin intense laser fields [J].J.Phys.B,1995,28:309.
[2] Posthumus J H.The dynamics of small molecules in intense laser fields[J].Rep.Prog.Phys.,2004,67:623.
[3] Bucksbaum P H,Zavriyev A,Muller H G,et al.Softening of themolecular bond in intense laser fields[J].Phys.Rev.Lett.,1990,64:1883.
[4] Fransinski L J,Posthumus J H,Plumridge J,et al.Manipulation of bond hardening inby chirping of intense pemtosecond laser pulses [J].Phys.Rev.Lett.,1999,83:3625.
[5] Jolicard G,Atabek O.Above-threshold-dissociation dynamics ofwith short intense laser pulses[J].Phys.Rev.A,1992,46:5845.
[6] Bandrauk A D,Zuo T.Charge-resonance-enhanced ionization of diatomic molecular ions by intense lasers[J].Phys.Rev.A,1995,52:R2511.
[7] Pariˇci^cD,Kiess A,Hänsch T W,et al.Intense-laser-field ionization of the hydrogen molecular ionsandat critical internuclear distances[J].Phys.Rev.Lett.,2005,94:163002.
[8] Sändig K,Figger H,Hänsch T W.Dissociation dynamics ofin intense laser fields:investigation of photofragments from single vibrational levels[J].Phys.Rev.Lett.,2000,85:4876.
[9] Staudte A,Bandrauk A D,Chelkowski S,et al.Attosecond strobing of two-surface population dynamics in dissociating[J].Phys.Rev.Lett.,2007,98:073003.
[10] Chelkowski S,Bandrauk A D,Staudte A,et al.Dynamic nuclear interference structures in the Coulomb explosion spectra of a hydrogen molecule in intense laser fields:Reexamination of molecular enhanced ionization[J].Phys.Rev.A,2007,76:013405.
[11] Serov V,Keller A,Atabek O,et al.Intense laser dissociation of:From experiment to theory[J].Phys.Rev.A,2005,72:033413.
[12] Ben-Itzhak I,Wang P Q,Xia J F,et al.Dissociation and ionization ofby ultrashort intense laser pulses probed by coincidence 3Dmomentum imaging[J].Phys.Rev.Lett.,2005,95:073002.
[13] Lu R F,Xiao C Y,Deng K M,et al.Coherent superposition in the coulomb explosion spectra of[J].Chem.Phys.2011,382;88.
[14] Du H N,Miao X Y.Theoretical exploration of intensity effects on high-order harmonic generation frommolecules[J].J.At.Mol.Phys.(原子与分子物理学报),2013,30(1):115(in Chinese)
[15] Liu S S,Miao X Y.Enhancement of high-order harmonic emission by using a coherent superposition in a two-color laser field[J].J.At.Mol.Phys.(原子与分子物理学报),2012,29(5):881(in Chinese)
[16] Lu R F,Zhang P Y,Han K L.Attosecond-resolution quantum dynamics calculations for atoms and molecules in strong laser fields[J].Phys.Rev.E,2008,77:066701.
[17] Sharafeddin O,Zhang Z H.A DVR based time-dependent wave packet treatment for reactive scattering[J].Chem.Phys.Lett.,1993,204:190.
[18] Feuerstein B,Thumm J.On the computation of momentum distributions within wavepacket propagation calculations[J].J.Phys.B,2003,36:707.
