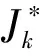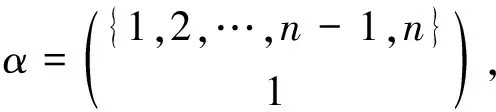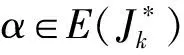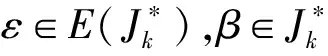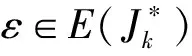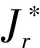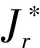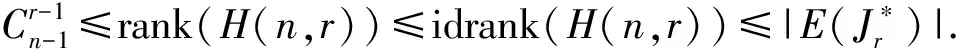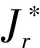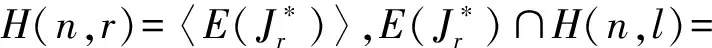半群Hn的每个星理想的秩和幂等元秩

罗永贵, 徐 波, 游泰杰

(贵州师范大学 数学与计算机科学学院, 贵州 贵阳 550001)

1 预备知识

通常一个有限半群S的秩定义为rank(S)=min{|A|:A⊆S,〈A〉=S}.如果S是由幂等元集E(S)生成的,那么S的幂等元秩定义为idrankS=min{|A|:A⊆E(S)⊆S,〈A〉=S}.半群S与它的子半群V之间的相关秩定义为r(S,V)=min{|A|:A⊆S,A∩V=Ø,〈A∪V〉=S}.对于有限半群的生成集、秩、幂等元秩及其相关秩的研究一直以来都是半群理论研究中的热点之一[1-14].

H(n,r)={α∈Hn:|Imα|≤r}, 1≤r≤n-1,

本文在文献[1-5]的基础上继续考虑保降序且保序有限奇异变换半群Hn的双边星理想H(n,r)的秩、幂等元秩及其相关秩,证明了如下主要结果.

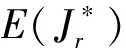
定理3设自然数n≥3,则有

r(H(n,r),H(n,l))=

设P、Q是自然序集Xn的非空子集,若对∀a∈P,b∈Q有a

其中,每个Ai(1≤i≤k)都是凸集,A1

为叙方便,这里引用Green*-等价关系[15].不难验证,在半群H(n,r)中L*、R*、J*具有如下刻划:对∀α,β∈H(n,r)有

(α,β)∈L*⟺Imα=Imβ,

(α,β)∈R*⟺kerα=kerβ,

(α,β)∈J*⟺|Imα|=|Imβ|.

本文未定义的术语及符号参见文献[16-18].

2 定理的证明

为完成定理的证明先给出若干引理与推论.

引理1[1]设α∈H(n,r)⊆Hn,则下列条件等价:

1)α是幂等元;

2) 对∀t∈Imα有t=min{x:x∈tα-1};

3)α|Im α是恒等变换.

证明以下分2种情形加以证明.

情形1当k=1时,令

情形2当2≤k≤r≤n-1,若α的标准表示如下:

其中,每个Ai(1≤i≤k)都是凸集,A1

对1≤i≤k,记ti=minAi.由于a1=1∈A1.以下分2种子情形讨论.

情形2.1如果a2∈A2,将考虑a3∈A3或a3∉A3.如果a2∉A2,注意到α∈H(n,r)及引理1,必有a2∈A1.令

情形2.2对1≤m≤i-1有am∈Am.如果ai∈Ai,将考虑ai+1∈Ai+1或ai+1∉Ai+1.如果ai∉Ai,注意到α∈H(n,r)及引理1,必有ai∈Ai-1.令

证明以下分2种情形加以证明.

情形3由引理2的情形1知

其中,每个Ai(1≤i≤k)都是凸集,A1

情形4.1若存在i∈{1,2,…,k-1,k}使得|Ai|≥3.可以选择b∈Ai使得b≠ai且b≠maxAi.令

情形4.2若存在m,p∈{1,2,…,i-1,i,i+1,…,k-1,k}使得m≠p,|Am|≥2且|Ap|≥2.令

引理4设α,β∈H(n,r),若(α,β),(α,αβ)∈J*,则(αβ,β)∈L*,(α,αβ)∈R*.

证明设α,β∈H(n,r),若(α,β),(α,αβ)∈J*,则|Imα|=|Imβ|=|Imαβ|.再由Im(αβ)⊆Imβ,kerα⊆ker (αβ)与Xn的有限性知,Im(αβ)=Imβ,kerα=ker(αβ),即(αβ,β)∈L*,(α,αβ)∈R*.

[1] 裴惠生,邹定宇,李连兵. 降序且保序的有限全变换半群[J]. 信阳师范学院学报:自然科学版,2006,19(4):373-377.

[2] Umar A. On the semigroups of order-decreasing finite full transformations[J]. Proc Royal Society of Edin,1992,A120:129-142.

[3] Umar A. On the ranks of certain finite semigroups of order-decreasing transformations[J]. Portugaliae Math,1996,53(1):23-34.

[4] Gomes G M S, Howie J M. On the ranks of certain semigroups of order-preserving transformations[J]. Semigroup Forum,1992,45(1):272-282.

[5] Garba G U. On the idempotent ranks of certain semigroups of order-preserving transformations[J]. Portugaliae Math,1994,51(2):185-204.

[6] Howie J M. Idempotent generators in finite full transformation semigroup[J]. Proc Royal Society of Edin,1978,A101:317-323.

[7] Howie J M, McFadden R B. Idenpotent rank in finite full transformation semigroup[J]. Proc Royal Society of Edin,1990,A114:161-167.

[8] Howie J M, Ruškuc N, Higgins P M. On Relative ranks of full transformation semigroups[J]. Commun Algebra,1998,26(3):733-748.

[9] 高荣海. 具有稳定子集的有限奇异变换半群的幂等生成元[J]. 四川师范大学学报:自然科学版,2010,33(6):778-783.

[10] 徐波,冯荣权,高荣海. 一类变换半群的秩[J]. 数学的实践与认识,2010,40(8):222-224.

[11] 高荣海,徐波. 关于保序压缩奇异变换半群的秩[J]. 山东大学学报:理学版,2011,46(6):4-7.

[12] 罗永贵,游泰杰,高荣海.关 于OIn和DOIn的理想的生成集及其秩[J]. 贵州师范大学学报:自然科学版,2012,30(2):9-12.

[13] 徐波. 正则保序压缩变换半群的秩[J]. 贵州师范大学学报:自然科学版,2012,30(3):52-54.

[14] 罗永贵. 半群DOn中理想的秩和相关秩[J]. 吉林大学学报:理学版,2013,51(1):69-73.

[15] Fountain J B. A bundant semigroups[J]. Proc London Math Soc,1982,44(3):103-129.

[16] Howie J M. Fundamentals of Semigroup Theory[M]. Oxford:Oxford University Press,1995.

[17] Ganyushkin O, Mazorchuk V. Classical Finite Transformation Semigroups[M]. London:Springer-Verlag,2009.

[18] Ruškuc N. Semigroup Presentations[D]. St Andrews:University of St Andrews,1995.