基于自抗扰控制器的风柴储微电网频率控制方法

曹 博，苏兴振，谭学菊

（中信戴卡股份有限公司，河北 秦皇岛611731）

频率稳定是微电网安全稳定运行的重要因素，它反映了微电网中有功功率供需平衡的基本状态［1].由于微电网中的风力发电等可再生能源的出力和系统负荷的多变性和不可预测性，使得要时刻保持微电网的系统供需平衡非常的困难，并且大多数分布式电源及储能系统都是经过电力电子接口接入微电网，从而造成微电网系统的惯性很弱，使得扰动发生后系统频率变化比较快［2]，频繁的扰动会使系统的频率失去稳定，严重的甚至会导致系统解列.因此，对微网孤岛运行模式时的频率控制方法进行研究是非常必要的［3-7].

笔者针对微电网孤岛运行时由于风电的间歇性、波动性和负荷的不可预测性，导致微电网的频率难以控制的问题，将负荷和风力发电机的波动作为干扰考虑在内，提出了基于自抗扰控制器的风柴储微电网频率控制方法.

1 风柴储微电网系统

风柴储微电网系统由三个部分组成：发电装置、储能装置和能量消耗装置.其中发电装置有风力发电机和柴油机，储能装置为储能电池，能量消耗装置是系统的负荷，并且风力发电机、储能电池等分布式电源都需要通过电力电子变换器才能够与微网系统网络相连，并且储能电池既可以充电也可以放电，是通过双向逆变器连接到微电网的，系统的结构如图1所示.

图1 风柴储微网系统结构图

2 自抗扰控制策略设计

2.1 风柴储微网频率控制结构

利用负荷预测和风力发电输出功率的预测信息，根据可能出现的负荷波动和风力发电输出功率的波动来提前安排风力发电机和柴油机的发电计划，使得其能够在微电网频率还未波动的情况下，提前动作，减小可能出现的有功功率供需之间的差额，从而减小了微电网可能出现的频率波动，考虑到预测信息与实际信息之间会有误差.因此，同时采用储能电池实时控制微电网的频率，最终控制目标是使得其频率稳定在额定值附近，其控制结构如图2所示，主要包括两个模块：风柴功率分配模块和储能电池实时控制模块.

图2 风柴储微网系统控制框图

2.1.1 风柴功率分配模块

风柴功率分配模块的主要任务是根据负荷和风力发电的预测信息，对风力发电机和柴油机输出功率进行分配，使得风力发电机和柴油机尽可能地跟踪功率的变化，也就是提前规划未来时间中的发电计划，使得柴油机和风力发电机能够提前动作，减小了可能出现的微网的频率波动.风柴功率分配的目标是：在使得有功功率供需之间的差额绝对值最小的前提下，尽可能利用可再生能源风能来发电.

2.1.2 储能电池控制模块

由于传统的储能电池采用的都是下垂控制方法，其本质就是一个比例控制器，如果下垂系数比较大，微电源出力会出现过调节的情况，则微电网稳定性很难保证；如果下垂系数比较小的话，由于控制信号的处理时间不能忽略不计，微电源来不及改变出力，此时，微电网频率也会出现较大的波动；并且下垂控制属于有差调节，其频率稳定值会偏离微电网的额定频率值，当偏离比较大时，会影响微电源甚至整个微网的安全稳定运行.最重要的是，由于微电网系统的频率控制受风力发电输出功率波动、负荷波动这些外部干扰和系统模型不够精确等内部干扰的影响比较大，而下垂控制没有办法抑制这些扰动，当扰动频繁出现时，会导致微电网运行崩溃.因此，需要对储能电池实时控制模块加以改进.笔者采用包含扩张状态观测器的抗干扰控制器，以保证功率快速、稳定的跟踪期望值.

2.2 基于自抗扰控制器的频率控制目标与结构

储能控制系统频率的目的是，抑制由于负荷和风力发电的波动而引起的系统频率波动，将微网的频率控制在额定值的附近，满足微电网对于频率波动的要求，使其能够安全稳定地运行.基于自抗扰控制器的储能电池频率控制结构如图3所示.

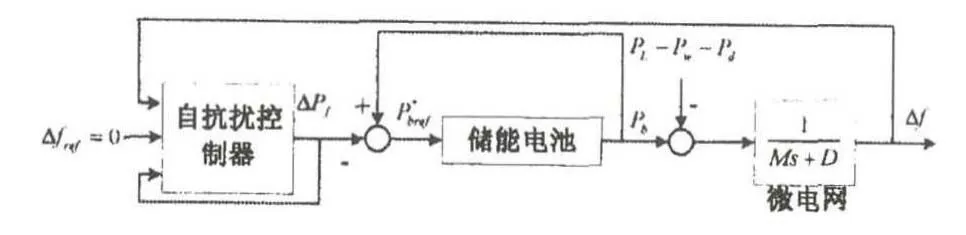
图3 基于自抗扰控制器的储能电池频率控制结构图

以设定值Δfref＝f-fref＝0为输入值，也就是系统设定值，其中fref为微网的额定频率值，f表示微网的实时频率值，ΔPf表示为了维持频率稳定储能电池需要调节的功率值，也就是系统的控制量；PL表示当前的微网负荷值，Pw表示当前的风力发电机输出功率，Pd表示当前的柴油机输出功率值，PL-Pw-Pd表示系统的干扰项，Δf表示系统的输出值.

2.3 基于自抗扰的储能电池频率控制器设计

根据图3中基于自抗扰控制器的储能电池频率控制结构可以看出，该控制结构的被控对象由储能电池和微网系统共同组成，由于储能电池能够等效为一阶滞后环节［8].因此，基于自抗扰控制器的储能电池频率控制的被控对象可以看作是两个一阶惯性系统的串联，为一个二阶系统.故本文采用二阶自抗扰控制器，其控制框图如图4所示，图中G0为被控对象，G1为自抗扰控制器的跟踪微分器，G2为自抗扰控制器的扩张状态观测器，G3为自抗扰控制器的非线性状态误差反馈规律.

图4 基于二阶自抗扰控制器的控制框图

2.3.1 控制对象G0

自抗扰控制器需要得到被控对象的状态空间表达式，由控制量u＝ΔPf到输出量y＝Δf的控制结构如图5所示.

图5 控制量u到输出量y的控制结构框图

其中，PL-Pw-Pd是系统的干扰项.自抗扰控制器的被控对象不包括干扰项，容易求出该控制结构的传递函数如式（1）所示.

G0（s）相应的状态空间表达式如式（2）所示.

其中x＝［x1，x2]＝［Δf，Pb]，输出y＝x1，控制量u＝ΔPf.

2.3.2 微分跟踪器G1

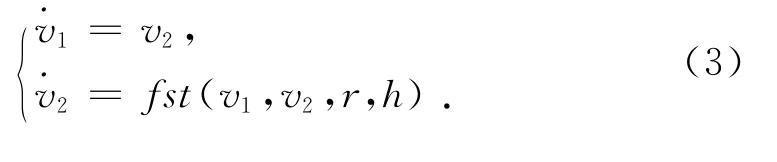
微分跟踪器对应的数学模型如式（3）所示.其中fst（v1，v2，r，h）函数由式（4）来确定，如下所示.

其中，sign函数为符号函数，r称为速度因子，它的取值可以决定跟踪的快慢，而h被称为滤波因子，在输入信号被噪声污染时，它的取值可以决定滤波的效果.由式（3）和（4）可知，微分跟踪器的可调参数是速度因子r和滤波因子h.

2.3.3 扩张状态观测器G2

扩张状态观测器对应的数学模型如式（5）所示，其中fal（ε，α，δ）函数如式（6）所示.

适当选择｛α1，α2，δ1，β01，β02，β03｝，就能够使得z1、z2很好地估计被控量y和dy，而z3则可以估计出扰动.

2.3.4 非线性状态误差反馈律G3

非线性状态误差反馈律的数学模型如式（7）所示.

其中，fal函数如式（6）所示，z3是受控系统中被扩张出来的状态变量，k1，k2，α3，α4，δ2为可调参数.

3 仿真和结果说明

利用MATLAB搭建基于自抗扰控制器的储能电池频率控制方法的模型.由于跟踪微分器、扩张状态观测器、非线性状态反馈规律都是相互独立设计的.因此，可以采用分离性原理来整定自抗扰控制器的参数.例如ESO的｛α1，α2，δ1｝和NLSEF的｛α3，α4，δ2｝都是可以根据实际运行经验取固定值的.选择α1＝0.5，α2＝0.25，δ1＝0；α3＝0.75，α4＝1.25，δ2＝0，r＝10，h＝0.01；β01＝210，β02＝8，β03＝0.2；k01＝12，k02＝0.02.

自抗扰控制算法与下垂控制算法的频率控制效果对比如图6所示，可以看出采用自抗扰控制器跟踪的风柴储微网的频率偏移量为0.001.这是由于自抗扰控制器通过扩张状态观测器观测了系统的扰动，也就是负荷和风力发电的波动，并且对该扰动进行实时补偿，抑制了负荷和风电波动对于频率的影响，使得风柴储微网的系统频率稳定在额定值.

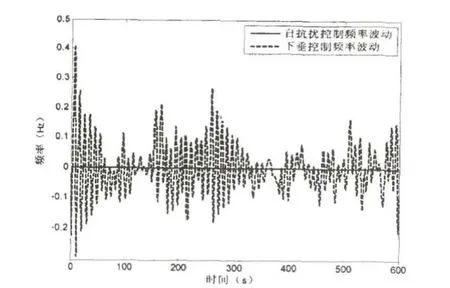
图6 频率控制效果对比图

自抗扰控制算法与下垂控制算法的储能电池充放电功率对比曲线如图7所示.由于下垂控制没有办法抑制负荷和风电的波动对系统频率的影响，因此，储能电池必须根据负荷和风力发电的波动进行充放电，从而使得储能电池的输出功率比较大；而采用自抗扰控制器的储能电池频率控制方法由于引入了扩张状态观测器实时地补偿了扰动，因此其充放电功率很小，在对比图中看起来基本上是一条直线，单独的自抗扰控制器的储能电池的输出功率曲线如图8所示.

图7 储能电池输出功率对比图

自抗扰控制算法与下垂控制算法的储能电池SOC对比曲线如图9所示，由于基于自抗扰控制器的储能电池的抗干扰能力强，其充放电功率比较小，因此其SOC基本维持在0.5附近，充放电动作没有下垂控制那么频繁.

图8 自抗扰控制器储能电池输出功率图

图9 储能SOC对比图

从上述仿真结果可以看出，基于自抗扰控制器的频率控制方法比传统的下垂控制方法控制频率的效果好，此时，微网的频率稳定在额定值附近.由于自抗扰控制器能够实时补偿风电和负荷波动干扰对于频率波动的影响，从而抑制了负荷和风电波动对微网频率造成的影响.因此相对于对比算法来说，自抗扰控制中储能电池的充放电功率会大幅度地减小，使得储能电池的SOC基本维持在0.5.

4 结论

针对微网孤岛运行时由于风电的间歇性、波动性和负荷的不可预测性导致微网的频率难以控制问题，笔者将负荷与风电的波动当作系统的干扰，将储能电池和微电网作为被控对象，设计了基于扩张状态观测器的实时频率补偿控制器.仿真结果表明该频率补偿控制器可以使得微电网的频率稳定在额定值附近.

［1]赵波，李鹏，童杭伟，等.从分布式发电到微网的研究综述［J].浙江电力，2010（3）：1-5.

［2]张建华，黄伟.微电网运行控制与保护技术［M].北京：中国电力出版社，2010.

［3]余洋，陈盈今，刘立卿，等.大规模风电接入对电网电压稳定性影响的研究［J].电力科学与工程，2010，26（4）：1-4.

［4]J A Peas Lopes，C L Moreira，A G Madureira.Defining control strategies for microgrids islanded operation［J].Power Systems，IEEE Transactions on，2006，21（2）：916-924.

［5]R Sebastian.Modelling and simulation of a high penetration wind diesel system with battery energy storage［J].International Journal of Electrical Power &Energy Systems，2011，33（3）：767-774.

［6]B Sedaghat，A Jalilvand，R Noroozian.Design of a predictive control strategy for integration of stand-alone wind／diesel system［C]／／Power and Energy（PECon），2010IEEE International Conference on.IEEE，2010：518-522.

［7]J A Carr，J C Balda，H A Mantooth.A survey of systems to integrate distributed energy resources and energy storage on the utility grid［C]／／Energy 2030Conference，2008.ENERGY 2008.IEEE.IEEE，2008：1-7.

［8]T Senjyu，A Uehara，A Yona，et al.Frequency control by coordination control of wind turbine generator and battery using H∞control［C]／／Transmission &Distribution Conference &Exposition：Asia and Pacific，2009.IEEE，2009：1-4.