运用插值法进行利率计算公式的解析

马 伟

(常州纺织服装职业技术学院，江苏 常州 213164)

财务管理课程中，用插值法进行利率计算，即知晓现值或终值系数，通过现值系数表或终值系数表，找出两个相邻的利率和其对应的系数，再通过插值的方式计算出利率的方法。一般财务管理课程的教材对这一方法仅通过文字叙述，然后给出相应的公式，并没有解释其由来，学生单纯记忆难以掌握。我们不妨通过插值法的公式推导，让学生在理解的基础上掌握插值法在利率计算中的公式。

假设需要求的利率为ix，其对应的已知系数为c，与ix相邻的两个利率和对应的系数分别为i1、c1和i2、c2，利率较小的为i1，利率较大的为i2。根据四张系数表进行推算。

一、现值系数表

复利现值系数表和年金现值系数表，如表1、表2 所示。

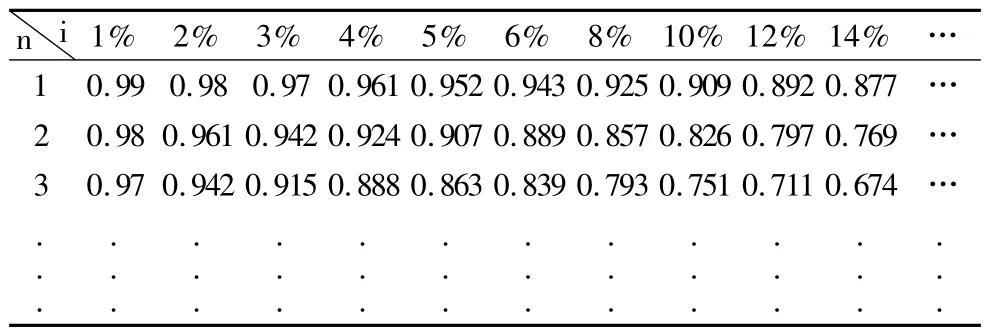
表1 复利现值系数表

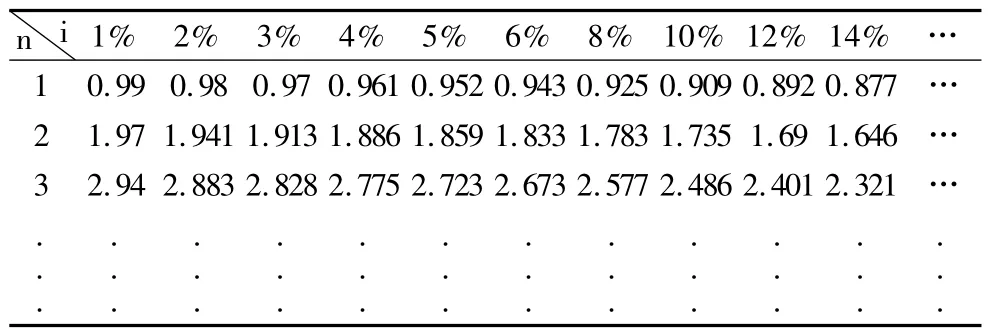
表2 年金现值系数表

表1 和表2 反映出，利率i 和利率对应的系数c成反方向变化，即现值系数表中，利率i 越大，系数c越小，反映在坐标系中，即图1 中的弧线，当弧线中的两点比较接近时，可以将弧线近视为直线。

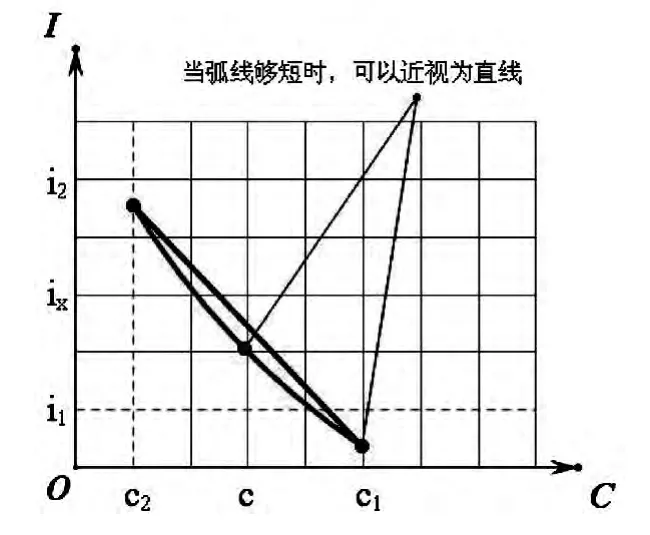
图1 现值系数图

将弧线近视为直线，分别在坐标系中取ix，c，i1、c1和i2、c2，将对应的利率和系数的交点如图连接起来，为两个相似三角形，如图2 所示。

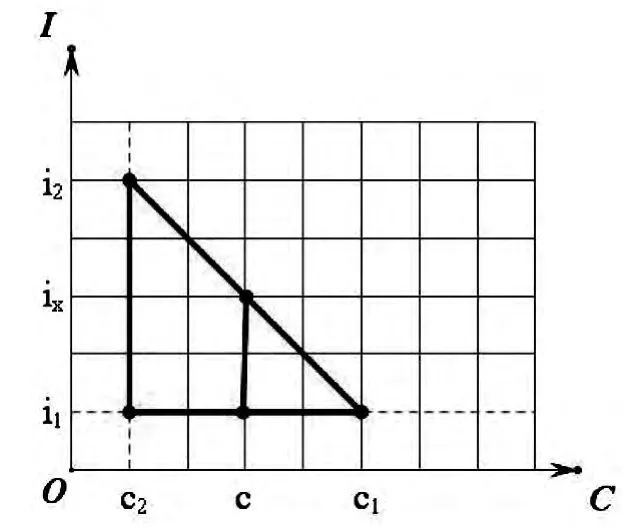
图2 现值系数近视图

在坐标系上，已知c1、c2、c、i1、i2，求ix，利用几何原理，两个相似三角形的对应边之比相等，列出等式一

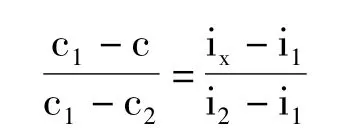
二、终值系数表

观察复利终值系数表和年金终值系数表，如表3、表4。

表3 复利终值系数表

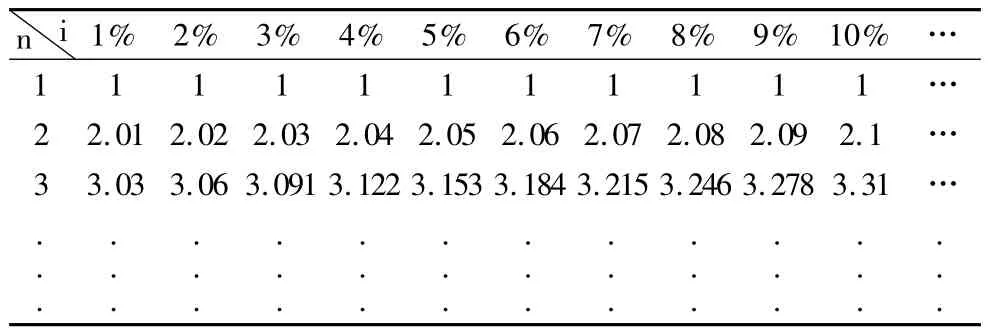
表4 年金终值系数表

表3 和表4 反映出，利率i 和利率对应的系数c成同方向变化，即终值系数表中，利率i 越大，系数c越大，反映在坐标系中即图3 中的弧线，当弧线中的两点比较接近时，可以将弧线近视为直线。

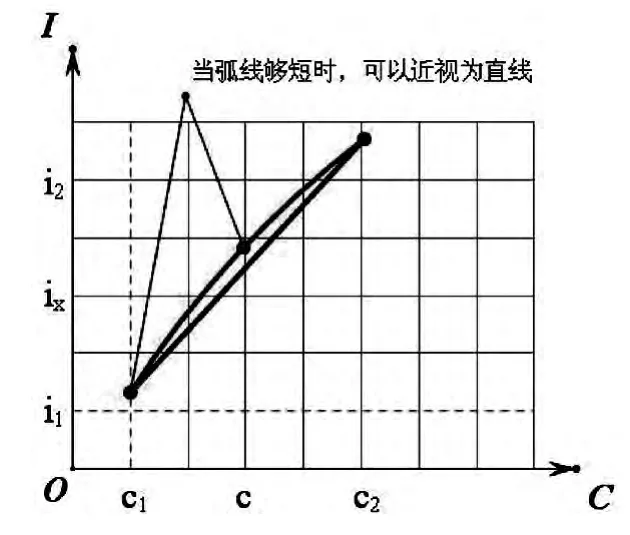
图3 终值系数图

将弧线近视为直线，同样，分别在坐标系中取ix，c，i1、c1和i2、c2，在坐标系中将对应的利率和系数的交点如图连接起来，为两个相似三角形，如图4 所示。

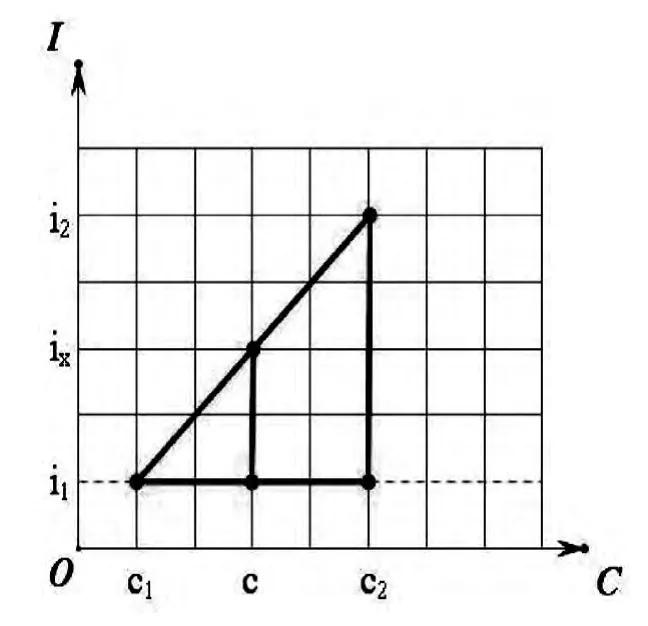
图4 终值系数近视图

在坐标系上，已知c1、c2、c、i1、i2，求ix，利用几何原理，两个相似三角形的对应边之比相等，列出等式二

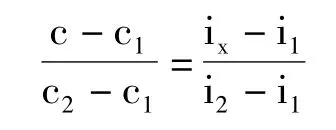
三、推导结论

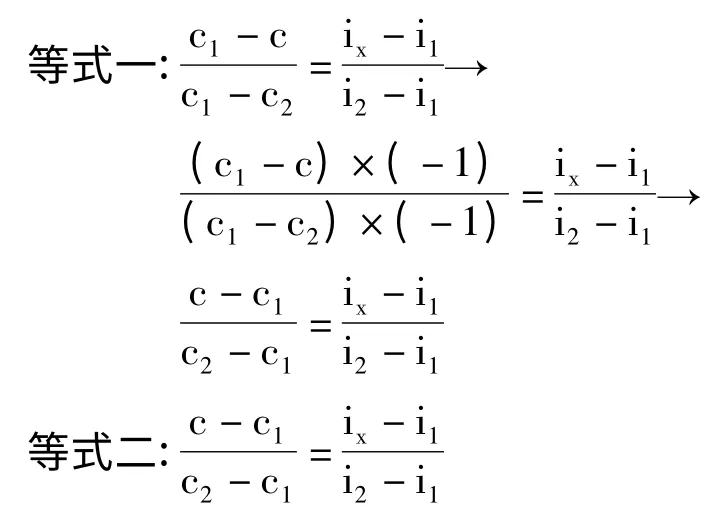
将等式一的左半边分子分母同乘以-1，等式一和等式二是一样的，求出:

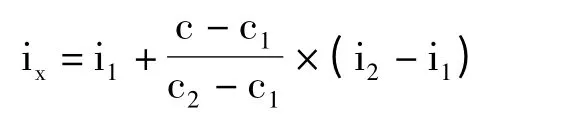
因此，复利现值、年金现值、复利终值、年金终值中，用插值法求利率，其只有如上一种公式。通过公式推导演示，学生很容易理解并掌握。

［1］曹惠民主编.财务管理学［M］.上海:立信会计出版社，2011.

［2］栾庆伟，迟国泰主编.财务管理［M］.大连:大连理工大学出版社，2008.